Aufgaben:Aufgabe 4.6: Koordinatendrehung: Unterschied zwischen den Versionen
Aus LNTwww
K (Guenter verschob die Seite 4.6 Koordinatendrehung nach Aufgabe 4.6: Koordinatendrehung) |
|||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID431__Sto_A_4_6_neu.png|right|Koordinatendrehung einer 2D-WDF]] | + | [[Datei:P_ID431__Sto_A_4_6_neu.png|right|frame|Koordinatendrehung einer 2D-WDF]] |
| − | Wir betrachten in der Aufgabe eine zweidimensionale Gaußsche Zufallsgröße $(x, y)$ mit statistisch unabhängigen Komponenten. Die Streuungen der beiden Komponenten seien $\sigma_x = 1$ und $\sigma_y = 2$. | + | Wir betrachten in der Aufgabe eine zweidimensionale Gaußsche Zufallsgröße $(x,\hspace{0.08cm} y)$ mit statistisch unabhängigen Komponenten. Die Streuungen der beiden Komponenten seien $\sigma_x = 1$ und $\sigma_y = 2$. |
| − | Berechnet werden soll die Wahrscheinlichkeit dafür, dass die zweidimensionale Zufallsgröße $(x, y)$ innerhalb des grün schraffiert eingezeichneten Bereichs liegt: | + | Berechnet werden soll die Wahrscheinlichkeit dafür, dass die zweidimensionale Zufallsgröße $(x,\hspace{0.08cm} y)$ innerhalb des grün schraffiert eingezeichneten Bereichs liegt: |
| − | :$$-C \le x + y \le C.$$ | + | :$$-C \le x + y \le +C.$$ |
Führen Sie zur Lösung eine Koordinatentransformation durch: | Führen Sie zur Lösung eine Koordinatentransformation durch: | ||
| Zeile 13: | Zeile 13: | ||
:$$\eta= -x +y .$$ | :$$\eta= -x +y .$$ | ||
| − | Dies entspricht einer Drehung des Koordinatensystems um $45^\circ$. Aus $x+y= \pm C$ folgt damit $\xi\pm C$. Die beiden zweidimensionalen Dichtefunktionen lauten dann: | + | Dies entspricht einer Drehung des Koordinatensystems um $45^\circ$. |
| − | :$$f_{xy} (x,y) = \frac{1}{4 \pi} \cdot \exp \left [ - ( x^2\hspace {-0.1cm} /2 + y^2\hspace {-0.1cm} /8) \right ] ,$$ | + | *Aus $x+y= \pm C$ folgt damit $\xi=\pm C$. |
| − | :$$f_{\xi\eta} (\xi, \eta) = \frac{1}{2 \pi \cdot \sigma_\xi \cdot \sigma_\eta \cdot \sqrt{1 - \rho_{\xi\eta}^2}} \cdot \exp \left [ - \frac{1}{2 \cdot (1 - \rho_{\xi\eta}^2)} \cdot ( \frac {\xi^2}{\sigma_\xi^2} + \frac {\eta^2}{\sigma_\eta^2 }- 2 \rho_{\xi\eta}\cdot \frac {\xi \cdot \eta}{\sigma_\xi \cdot \sigma_\eta}) \right ] .$$ | + | *Die beiden zweidimensionalen Dichtefunktionen lauten dann: |
| + | :$$f_{xy} (x,\hspace{0.08cm}y) = \frac{1}{4 \pi} \cdot \exp \left [ - ( x^2\hspace {-0.1cm} /2 + y^2\hspace {-0.1cm} /8) \right ] ,$$ | ||
| + | :$$f_{\xi\eta} (\xi,\hspace{0.08cm} \eta) = \frac{1}{2 \pi \cdot \sigma_\xi \cdot \sigma_\eta \cdot \sqrt{1 - \rho_{\xi\eta}^2}} \cdot \exp \left [ - \frac{1}{2 \cdot (1 - \rho_{\xi\eta}^2)} \cdot ( \frac {\xi^2}{\sigma_\xi^2} + \frac {\eta^2}{\sigma_\eta^2 }- 2 \rho_{\xi\eta}\cdot \frac {\xi \cdot \eta}{\sigma_\xi \cdot \sigma_\eta}) \right ] .$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen|Zweidimensionale Gaußsche Zufallsgrößen]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen#Drehung_des_Koordinatensystems|Drehung des Koordinatensystems]]. | ||
| + | |||
| + | *Gegeben sind die Näherungen ${\rm Q}(2.3) \approx 0.01$ und ${\rm Q}(2.6) \approx 0.005$ für das komplementäre Gaußsche Fehlerintegral. | ||
| + | *Weitere Informationen zu dieser Thematik liefert das Lernvideo [[Gaußsche_2D-Zufallsgrößen_(Lernvideo)|Gaußsche 2D-Zufallsgrößen]]: | ||
| + | ::Teil 1: Gaußsche Zufallsgrößen ohne statistische Bindungen, | ||
| + | ::Teil 2: Gaußsche Zufallsgrößen mit statistischen Bindungen. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 31: | Zeile 38: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Ermitteln Sie durch Koeffizientenvergleich das Verhältnis der beiden Streuungen der neuen Zufallsgröße $(\xi, \eta)$. | + | {Ermitteln Sie durch Koeffizientenvergleich das Verhältnis der beiden Streuungen der neuen Zufallsgröße $(\xi,\hspace{0.08cm} \eta)$. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_\xi/\sigma_\eta \ = $ { 1 3% } | + | $\sigma_\xi/\sigma_\eta \ = \ $ { 1 3% } |
| − | {Berechnen Sie die Streuung $\sigma_\xi$ und den Korrelationskoeffizienten $\rho_{\xi\eta}$ zwischen den neuen Zufallsgrößen $\xi$ und $\eta$. | + | {Berechnen Sie die Streuung $\sigma_\xi$ und den Korrelationskoeffizienten $\rho_{\xi\eta}$ zwischen den neuen Zufallsgrößen $\xi$ und $\eta$. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_\xi \ = $ { 2.236 3% } | + | $\sigma_\xi \ = \ $ { 2.236 3% } |
| − | $\rho_{\xi\eta} \ = $ { 0.6 3% } | + | $\rho_{\xi\eta} \ = \ $ { 0.6 3% } |
| − | {Berechnen Sie die Wahrscheinlichkeit, dass $ |x+y| \le C$ gilt. Wie groß ist $C$ zu wählen, damit $99\%$ aller Größen im schraffierten Bereich liegen? | + | {Berechnen Sie die Wahrscheinlichkeit, dass $ |\hspace{0.05cm}x+y\hspace{0.05cm}| \le C$ gilt. Wie groß ist $C$ zu wählen, damit $99\%$ aller Größen im schraffierten Bereich liegen? |
|type="{}"} | |type="{}"} | ||
| − | $C_{99\%} \ = $ { 5.814 3% } | + | $C_{99\%} \ = \ $ { 5.814 3% } |
| Zeile 51: | Zeile 58: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Aus $\xi = x + y$ und $\eta = -x + y$ folgt direkt: | + | '''(1)''' Aus $\xi = x + y$ und $\eta = -x + y$ folgt direkt: |
:$$x = {1}/{2} \cdot ( \xi - \eta ) ,\hspace{0.5cm}y = {1}/{2}\cdot ( \xi +\eta ) .$$ | :$$x = {1}/{2} \cdot ( \xi - \eta ) ,\hspace{0.5cm}y = {1}/{2}\cdot ( \xi +\eta ) .$$ | ||
| − | Setzt man diese Werte für den negativen Exponenten ein, so erhält man: | + | *Setzt man diese Werte für den negativen Exponenten ein, so erhält man: |
:$$\frac{x^2}{2} + \frac{y^2}{8} = \frac{1}{8} \cdot ( \xi - \eta )^2 + \frac{1}{32} \cdot ( \xi + \eta )^2.$$ | :$$\frac{x^2}{2} + \frac{y^2}{8} = \frac{1}{8} \cdot ( \xi - \eta )^2 + \frac{1}{32} \cdot ( \xi + \eta )^2.$$ | ||
| − | Ausmultipliziert ergibt dies: | + | *Ausmultipliziert ergibt dies: |
:$$\frac{5}{32} \cdot \xi^2 + \frac{5}{32} \cdot \eta^2 - \frac{3}{16} \cdot \xi \cdot \eta .$$ | :$$\frac{5}{32} \cdot \xi^2 + \frac{5}{32} \cdot \eta^2 - \frac{3}{16} \cdot \xi \cdot \eta .$$ | ||
| − | Da die Koeffizienten bei $\xi^2$ und $\eta^2$ gleich sind, gilt $\sigma_\xi = \sigma_\eta$ <u>Der gesuchte Quotient ist somit 1</u>. | + | *Da die Koeffizienten bei $\xi^2$ und $\eta^2$ gleich sind, gilt $\sigma_\xi = \sigma_\eta$. <u>Der gesuchte Quotient ist somit 1</u>. |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Durch Koeffizientenvergleich erhält man für $\sigma_\xi = \sigma_\eta$ das Gleichungssystem: | ||
| + | :$$2 \cdot \sigma_\xi^2 \cdot (1 - \rho_{\xi\eta}^2)= \frac{32}{5},$$ | ||
| + | :$$\frac{\sigma_\xi^2 \cdot (1 - \rho_{\xi\eta}^2)}{\rho_{\xi\eta}}= \frac{16}{3}.$$ | ||
| + | |||
| + | *Setzt man die erste Gleichung in die zweite ein, so ergibt sich $\rho_{\xi\eta}\hspace{0.15cm}\underline {= 0.6}$ und $\sigma_{\xi} = \sqrt{5}\hspace{0.15cm}\underline {= 2.236}$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
'''(3)''' Nach Koordinatentransformation kann man für diese Wahrscheinlichkeit schreiben: | '''(3)''' Nach Koordinatentransformation kann man für diese Wahrscheinlichkeit schreiben: | ||
:$${\rm Pr} ( | x + y | \le C ) = {\rm Pr} ( | \xi | \le C ) = 1 - 2 \cdot {\rm Pr} ( \xi >C ).$$ | :$${\rm Pr} ( | x + y | \le C ) = {\rm Pr} ( | \xi | \le C ) = 1 - 2 \cdot {\rm Pr} ( \xi >C ).$$ | ||
| − | Mit dem komplementären Gaußschen Fehlerintegral folgt daraus weiter: | + | *Mit dem komplementären Gaußschen Fehlerintegral folgt daraus weiter: |
:$${\rm Pr} ( | x + y | \le C ) = 1 - 2 \cdot {\rm Q} ( {C}/{\sigma_\xi}) = 0.99 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q} ( {C}/{\sigma_\xi}) = 0.005.$$ | :$${\rm Pr} ( | x + y | \le C ) = 1 - 2 \cdot {\rm Q} ( {C}/{\sigma_\xi}) = 0.99 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q} ( {C}/{\sigma_\xi}) = 0.005.$$ | ||
| − | Mit dem angegebenen Wert ${\rm Q}(2.6) \approx 0.005$ erhält man somit das Ergebnis: $C \approx 2.6 \cdot \sigma_{\xi}\hspace{0.15cm}\underline {= 5.814}$ | + | *Mit dem angegebenen Wert ${\rm Q}(2.6) \approx 0.005$ erhält man somit das Ergebnis: |
| + | :$$C \approx 2.6 \cdot \sigma_{\xi}\hspace{0.15cm}\underline {= 5.814}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 24. Februar 2022, 18:12 Uhr
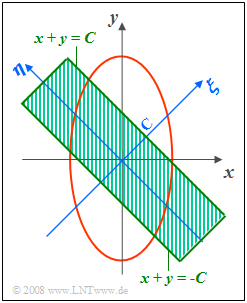
Wir betrachten in der Aufgabe eine zweidimensionale Gaußsche Zufallsgröße $(x,\hspace{0.08cm} y)$ mit statistisch unabhängigen Komponenten. Die Streuungen der beiden Komponenten seien $\sigma_x = 1$ und $\sigma_y = 2$.
Berechnet werden soll die Wahrscheinlichkeit dafür, dass die zweidimensionale Zufallsgröße $(x,\hspace{0.08cm} y)$ innerhalb des grün schraffiert eingezeichneten Bereichs liegt:
- $$-C \le x + y \le +C.$$
Führen Sie zur Lösung eine Koordinatentransformation durch:
- $$\xi = \hspace{0.4cm} x +y,$$
- $$\eta= -x +y .$$
Dies entspricht einer Drehung des Koordinatensystems um $45^\circ$.
- Aus $x+y= \pm C$ folgt damit $\xi=\pm C$.
- Die beiden zweidimensionalen Dichtefunktionen lauten dann:
- $$f_{xy} (x,\hspace{0.08cm}y) = \frac{1}{4 \pi} \cdot \exp \left [ - ( x^2\hspace {-0.1cm} /2 + y^2\hspace {-0.1cm} /8) \right ] ,$$
- $$f_{\xi\eta} (\xi,\hspace{0.08cm} \eta) = \frac{1}{2 \pi \cdot \sigma_\xi \cdot \sigma_\eta \cdot \sqrt{1 - \rho_{\xi\eta}^2}} \cdot \exp \left [ - \frac{1}{2 \cdot (1 - \rho_{\xi\eta}^2)} \cdot ( \frac {\xi^2}{\sigma_\xi^2} + \frac {\eta^2}{\sigma_\eta^2 }- 2 \rho_{\xi\eta}\cdot \frac {\xi \cdot \eta}{\sigma_\xi \cdot \sigma_\eta}) \right ] .$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Gaußsche Zufallsgrößen.
- Bezug genommen wird insbesondere auf die Seite Drehung des Koordinatensystems.
- Gegeben sind die Näherungen ${\rm Q}(2.3) \approx 0.01$ und ${\rm Q}(2.6) \approx 0.005$ für das komplementäre Gaußsche Fehlerintegral.
- Weitere Informationen zu dieser Thematik liefert das Lernvideo Gaußsche 2D-Zufallsgrößen:
- Teil 1: Gaußsche Zufallsgrößen ohne statistische Bindungen,
- Teil 2: Gaußsche Zufallsgrößen mit statistischen Bindungen.
Fragebogen
Musterlösung
(1) Aus $\xi = x + y$ und $\eta = -x + y$ folgt direkt:
- $$x = {1}/{2} \cdot ( \xi - \eta ) ,\hspace{0.5cm}y = {1}/{2}\cdot ( \xi +\eta ) .$$
- Setzt man diese Werte für den negativen Exponenten ein, so erhält man:
- $$\frac{x^2}{2} + \frac{y^2}{8} = \frac{1}{8} \cdot ( \xi - \eta )^2 + \frac{1}{32} \cdot ( \xi + \eta )^2.$$
- Ausmultipliziert ergibt dies:
- $$\frac{5}{32} \cdot \xi^2 + \frac{5}{32} \cdot \eta^2 - \frac{3}{16} \cdot \xi \cdot \eta .$$
- Da die Koeffizienten bei $\xi^2$ und $\eta^2$ gleich sind, gilt $\sigma_\xi = \sigma_\eta$. Der gesuchte Quotient ist somit 1.
(2) Durch Koeffizientenvergleich erhält man für $\sigma_\xi = \sigma_\eta$ das Gleichungssystem:
- $$2 \cdot \sigma_\xi^2 \cdot (1 - \rho_{\xi\eta}^2)= \frac{32}{5},$$
- $$\frac{\sigma_\xi^2 \cdot (1 - \rho_{\xi\eta}^2)}{\rho_{\xi\eta}}= \frac{16}{3}.$$
- Setzt man die erste Gleichung in die zweite ein, so ergibt sich $\rho_{\xi\eta}\hspace{0.15cm}\underline {= 0.6}$ und $\sigma_{\xi} = \sqrt{5}\hspace{0.15cm}\underline {= 2.236}$.
(3) Nach Koordinatentransformation kann man für diese Wahrscheinlichkeit schreiben:
- $${\rm Pr} ( | x + y | \le C ) = {\rm Pr} ( | \xi | \le C ) = 1 - 2 \cdot {\rm Pr} ( \xi >C ).$$
- Mit dem komplementären Gaußschen Fehlerintegral folgt daraus weiter:
- $${\rm Pr} ( | x + y | \le C ) = 1 - 2 \cdot {\rm Q} ( {C}/{\sigma_\xi}) = 0.99 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q} ( {C}/{\sigma_\xi}) = 0.005.$$
- Mit dem angegebenen Wert ${\rm Q}(2.6) \approx 0.005$ erhält man somit das Ergebnis:
- $$C \approx 2.6 \cdot \sigma_{\xi}\hspace{0.15cm}\underline {= 5.814}.$$