Aufgabe 4.5Z: Einfacher Phasenmodulator
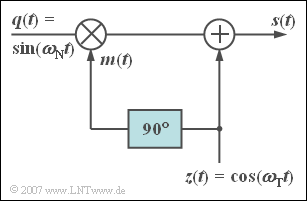
Die Grafik zeigt eine recht einfache Anordnung zur Approximation eines Phasenmodulators. Alle Signale seien hierbei dimensionslose Größen.
Das sinusförmige Nachrichtensignal $q(t)$ der Frequenz $f_{\rm N} = 10 \ \text{kHz}$ wird mit dem Signal $m(t)$ multipliziert, das sich aus dem cosinusförmigen Trägersignal $z(t)$ durch Phasenverschiebung um $\phi = 90^\circ$ ergibt:
- $$m(t) = {\cos} ( \omega_{\rm T} \cdot t + 90^\circ).$$
Anschließend wird das Signal $z(t)$ mit der Frequenz $f_{\rm T} = 1 \ \text{MHz}$ noch direkt addiert.
Zur Abkürzung werden in dieser Aufgabe auch verwendet:
- die Differenzfrequenz $f_{\rm \Delta} = f_{\rm T} - f_{\rm N} = 0.99 \ \text{MHz}$,
- die Summenfrequenz $f_{\rm \Sigma} = f_{\rm T} + f_{\rm N} = 1.01\ \text{MHz}$,
- die beiden Kreisfrequenzen $\omega_{\rm \Delta} = 2\pi \cdot f_{\rm \Delta}$ und $\omega_{\rm \Sigma} = 2\pi \cdot f_{\rm \Sigma}$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion.
- Berücksichtigen Sie die trigonomischen Umformungen
- $$\sin(\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \sin(\alpha - \beta) + {1}/{2} \cdot \sin(\alpha + \beta),$$
- $$\sin(\alpha) \cdot \sin (\beta)= {1}/{2} \cdot \cos(\alpha - \beta) - {1}/{2} \cdot \cos(\alpha + \beta).$$
Fragebogen
Musterlösung
- Durch die Phasenverschiebung um $\phi = 90^\circ$ wird aus der Cosinusfunktion die Minus–Sinusfunktion.
- Mit $q(t) = \sin(\omega_{\rm N} t)$ gilt:
- $${s(t)} = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - \sin({ \omega_{\rm T}\hspace{0.05cm} t }) \cdot \sin({ \omega_{\rm N}\hspace{0.05cm} t }) = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - 0.5 \cdot \cos(({ \omega_{\rm T}-\omega_{\rm N})\hspace{0.05cm} t }) + 0.5 \cdot \cos(({ \omega_{\rm T}+\omega_{\rm N})\hspace{0.05cm} t }).$$
(2) Das Spektrum des analytischen Signals lautet:
- $$S_{\rm +}(f) = \delta (f - f_{\rm T}) - 0.5 \cdot \delta (f - f_{\rm \Delta})+ 0.5 \cdot \delta (f - f_{\rm \Sigma}) .$$
- Durch Verschiebung um $f_{\rm T}$ kommt man zum Spektrum des äquivalenten Tiefpass-Signals:
- $$S_{\rm TP}(f) = \delta (f ) - 0.5 \cdot \delta (f + f_{\rm N})+ 0.5 \cdot \delta (f - f_{\rm N}) .$$
- Dies führt zu der Zeitfunktion
- $$s_{\rm TP}(t) = {\rm 1 } - 0.5 \cdot {\rm e}^{{-\rm j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t }+ 0.5 \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t } = 1 + {\rm j} \cdot \sin(\omega_{\rm N} \hspace{0.05cm} t ).$$
- Zum Zeitpunkt $t = 0$ ist $s_{\rm TP}(t) = 1$, also reell. Somit gilt:
- $s_{\rm I}(t = 0) = \text{Re}[s_{\rm TP}(t = 0)]\; \underline{= 1}$,
- $s_{\rm Q}(t = 0) = \text{Ime}[s_{\rm TP}(t = 0)]\; \underline{= 0}$.
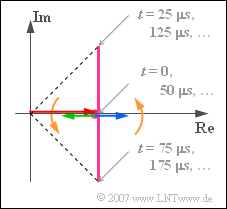
(3) Die Ortskurve ist eine vertikale Gerade ⇒ Vorschlag 3 mit folgenden Werten:
- $$s_{\rm TP}(t = 0) = s_{\rm TP}(t = {\rm 50 \hspace{0.05cm} µ s}) = \text{ ...} = 1,$$
- $$s_{\rm TP}(t = {\rm 25 \hspace{0.05cm} µ s}) = s_{\rm TP}(t = {\rm 125 \hspace{0.05cm} \mu s}) = \text{ ...} = 1 + {\rm j},$$
- $$s_{\rm TP}(t = {\rm 75 \hspace{0.05cm} µ s}) = s_{\rm TP}(t = {\rm 175 \hspace{0.05cm} \mu s}) = \text{ ...} = 1 - {\rm j}.$$
(4) Der Betrag (die Zeigerlänge) schwankt zwischen $a_{\rm max} = \sqrt{2}\; \underline{\approx 1.414}$ und $a_{\rm min} \;\underline{= 1}$. Es gilt:
- $$a(t) = \sqrt{1 + \sin^2(\omega_{\rm N} \hspace{0.05cm} t )}.$$
Bei idealer Phasenmodulation müsste dagegen die Hüllkurve $a(t)$ konstant sein.
(5) Der Realteil ist stets $1$, der Imaginärteil gleich $\sin(\omega_{\rm N} \cdot t) $. Daraus folgt die Phasenfunktion:
- $$\phi(t)= {\rm arctan} \hspace{0.1cm}{\left(\sin(\omega_{\rm N} \hspace{0.05cm} t )\right)}.$$
- Der Maximalwert der Sinusfunktion ist $1$. Daraus folgt:
- $$\phi_{\rm max} = \arctan (1) \; \underline{= \pi /4 } \; \Rightarrow \; \underline{45^\circ}.$$