Aufgaben:Aufgabe 4.5: Koaxialkabel – Impulsantwort: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
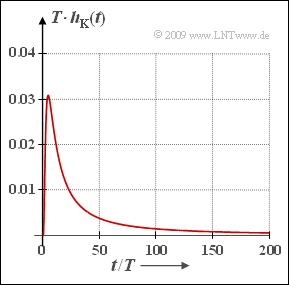
[[Datei:P_ID1814__LZI_A_4_5.png|right|frame|Impulsantwort eines Koaxialkabels]] | [[Datei:P_ID1814__LZI_A_4_5.png|right|frame|Impulsantwort eines Koaxialkabels]] | ||
| − | Der Frequenzgang eines Koaxialkabels der Länge $l$ ist durch folgende Formel darstellbar: | + | Der Frequenzgang eines Koaxialkabels der Länge $l$ ist durch folgende Formel darstellbar: |
:$$H_{\rm K}(f) = {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} | :$$H_{\rm K}(f) = {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} | ||
\cdot | \cdot | ||
| Zeile 10: | Zeile 10: | ||
{\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} | {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Der erste Term dieser Gleichung ist auf die Ohmschen Verluste zurückzuführen, der zweite Term auf die Querverluste. Dominant ist jedoch der Skineffekt, der durch den dritten Term ausgedrückt wird. | + | Der erste Term dieser Gleichung ist auf die Ohmschen Verluste zurückzuführen, der zweite Term auf die Querverluste. Dominant ist jedoch der Skineffekt, der durch den dritten Term ausgedrückt wird. |
| − | Mit den für ein | + | Mit den für ein „Normalkoaxialkabel” $\text{(2.6 mm}$ Kerndurchmesser, $\text{9.5 mm}$ Außendurchmesser$)$ gültigen Koeffizienten |
:$$\alpha_2 = 0.2722 \hspace{0.15cm}\frac {\rm Np}{\rm km \cdot \sqrt{\rm MHz}} | :$$\alpha_2 = 0.2722 \hspace{0.15cm}\frac {\rm Np}{\rm km \cdot \sqrt{\rm MHz}} | ||
\hspace{0.05cm}, | \hspace{0.05cm}, | ||
| Zeile 23: | Zeile 23: | ||
\hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} | \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ⇒ Dämpfungsverlauf ${a}_{\rm K}(f)$ und Phasenverlauf $b_{\rm K}(f)$ sind bis auf die Pseudoeinheiten „Np” bzw. „rad” identisch. | |
| − | Definiert man die charakteristische Kabeldämpfung ${a}_{\rm *}$ bei der halben Bitrate (also bei $R/2$ | + | Definiert man die charakteristische Kabeldämpfung ${a}_{\rm *}$ bei der halben Bitrate $($also bei $R/2)$ und normiert die Frequenz auf $R$, so kann man Digitalsysteme unterschiedlicher Bitrate und Länge einheitlich behandeln: |
:$${a}_{\rm \star} = {a}_{\rm K}(f ={R}/{2}) | :$${a}_{\rm \star} = {a}_{\rm K}(f ={R}/{2}) | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- | ||
{a}_{\rm \star} \cdot \sqrt{2f/R}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} {a}_{\star} \cdot \sqrt{2f/R}}\hspace{0.4cm}{\rm mit}\hspace{0.2cm}{a}_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} | {a}_{\rm \star} \cdot \sqrt{2f/R}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} {a}_{\star} \cdot \sqrt{2f/R}}\hspace{0.4cm}{\rm mit}\hspace{0.2cm}{a}_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Der entsprechende $\rm dB$–Wert ist um den Faktor $8.686$ größer. Bei einem Binärsystem gilt $R = 1/T$, so dass sich die charakteristische Kabeldämpfung auf die Frequenz $f = 1/(2T)$ bezieht. | + | *Der entsprechende $\rm dB$–Wert ist um den Faktor $8.686$ größer. |
| + | *Bei einem Binärsystem gilt $R = 1/T$, so dass sich die charakteristische Kabeldämpfung auf die Frequenz $f = 1/(2T)$ bezieht. | ||
| − | Die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Fouriertransformation|Fouriertransformierte]] von $H_{\rm K}(f)$ liefert die Impulsantwort $h_{\rm K}(t)$, die für ein Koaxialkabel mit den hier beschriebenen Näherungen in geschlossen–analytischer Form angebbar ist. Für ein Binärsystem gilt: | + | |
| + | Die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Fouriertransformation|Fouriertransformierte]] von $H_{\rm K}(f)$ liefert die Impulsantwort $h_{\rm K}(t)$, die für ein Koaxialkabel mit den hier beschriebenen Näherungen in geschlossen–analytischer Form angebbar ist. Für ein Binärsystem gilt: | ||
:$$h_{\rm K}(t) = \frac{ {a}_{\rm \star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot | :$$h_{\rm K}(t) = \frac{ {a}_{\rm \star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot | ||
| − | {\rm | + | {\rm e}^{ - {{a}_{\rm \star}^2}/(2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm} t/T)} |
\hspace{0.4cm}{\rm mit}\hspace{0.2cm}{a}_{\rm \star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} | \hspace{0.4cm}{\rm mit}\hspace{0.2cm}{a}_{\rm \star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die Teilaufgabe (5) bezieht sich auf den Empfangsgrundimpuls $g_r(t) = g_s(t) \star h_{\rm K}(t)$, wobei für $g_s(t)$ ein | + | Die Teilaufgabe '''(5)''' bezieht sich auf den Empfangsgrundimpuls $g_r(t) = g_s(t) \star h_{\rm K}(t)$, wobei für $g_s(t)$ ein Rechteck mit Höhe $s_0$ und Dauer $T$ angenommen wird. |
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Eigenschaften_von_Koaxialkabeln|Eigenschaften von Koaxialkabeln]]. | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Eigenschaften_von_Koaxialkabeln|Eigenschaften von Koaxialkabeln]]. |
| − | + | ||
| − | *Sie können zur Überprüfung Ihrer Ergebnisse das interaktive Applet [[Applets:Zeitverhalten_von_Kupferkabeln|Zeitverhalten von Kupferkabeln]] benutzen. | + | *Sie können zur Überprüfung Ihrer Ergebnisse das interaktive SWF–Applet [[Applets:Zeitverhalten_von_Kupferkabeln|Zeitverhalten von Kupferkabeln]] benutzen. |
| Zeile 53: | Zeile 55: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die Länge $l$ eines Normalkoaxialkabels, wenn sich für die Bitrate $R = 140 \ \rm Mbit/s$ die charakteristische Kabeldämpfung ${a}_{\rm \star} = 60 \ \rm dB$ ergibt? | + | {Wie groß ist die Länge $l$ eines Normalkoaxialkabels, wenn sich für die Bitrate $R = 140 \ \rm Mbit/s$ die charakteristische Kabeldämpfung ${a}_{\rm \star} = 60 \ \rm dB$ ergibt? |
|type="{}"} | |type="{}"} | ||
$l \ =\ $ { 3 3% } $\ \rm km$ | $l \ =\ $ { 3 3% } $\ \rm km$ | ||
| − | {Zu welcher Zeit $t_{\rm max}$ besitzt $h_{\rm K}(t)$ sein Maximum? Es gelte weiter ${a}_{\rm \star} = 60 \ \rm dB$. | + | {Zu welcher Zeit $t_{\rm max}$ besitzt $h_{\rm K}(t)$ sein Maximum? Es gelte weiter ${a}_{\rm \star} = 60 \ \rm dB$. |
|type="{}"} | |type="{}"} | ||
$t_{\rm max} \ = \ $ { 5 3% } $\ \cdot T$ | $t_{\rm max} \ = \ $ { 5 3% } $\ \cdot T$ | ||
| Zeile 65: | Zeile 67: | ||
{Wie groß ist der Maximalwert der Impulsantwort? | {Wie groß ist der Maximalwert der Impulsantwort? | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Max}\, [h_{\rm K}(t)] \ = \ $ { 0.03 3% } $\ \cdot 1/T$ | + | ${\rm Max}\, \big [h_{\rm K}(t)\big ] \ = \ $ { 0.03 3% } $\ \cdot 1/T$ |
| − | {Ab welcher Zeit $t_{\rm 5\%}$ ist $h_{\rm K}(t)$ kleiner als $5\%$ des Maximums? Berücksichtigen Sie als Näherung nur den ersten Term der angegebenen Formel. | + | {Ab welcher Zeit $t_{\rm 5\%}$ ist $h_{\rm K}(t)$ kleiner als $5\%$ des Maximums? Berücksichtigen Sie als Näherung nur den ersten Term der angegebenen Formel. |
|type="{}"} | |type="{}"} | ||
$t_{\rm 5\%} \ = \ $ { 103.5 3% } $\ \cdot T$ | $t_{\rm 5\%} \ = \ $ { 103.5 3% } $\ \cdot T$ | ||
| − | {Welche Aussagen treffen für den Empfangsgrundimpuls $g_r(t)$ zu? | + | {Welche Aussagen treffen für den Empfangsgrundimpuls $g_r(t)$ zu? |
|type="[]"} | |type="[]"} | ||
| − | - $g_r(t)$ ist doppelt so breit wie $h_{\rm K}(t)$. | + | - $g_r(t)$ ist doppelt so breit wie $h_{\rm K}(t)$. |
| − | + Es gilt näherungsweise $g_r(t) = s_0 \cdot T \cdot h_{\rm K}(t)$. | + | + Es gilt näherungsweise $g_r(t) = s_0 \cdot T \cdot h_{\rm K}(t)$. |
| − | - $g_r(t)$ kann durch einen Gaußimpuls angenähert werden. | + | - $g_r(t)$ kann durch einen Gaußimpuls angenähert werden. |
| Zeile 85: | Zeile 87: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die charakteristische Kabeldämpfung ${a}_{\rm \star} = 60 \ \rm dB$ entspricht in etwa $6.9\ \rm Np$. Deshalb muss gelten: | + | '''(1)''' Die charakteristische Kabeldämpfung ${a}_{\rm \star} = 60 \ \rm dB$ entspricht in etwa $6.9\ \rm Np$. Deshalb muss gelten: |
:$$\alpha_2 \cdot l \cdot {R}/{2} = 6.9\,\,{\rm | :$$\alpha_2 \cdot l \cdot {R}/{2} = 6.9\,\,{\rm | ||
Np} | Np} | ||
| Zeile 92: | Zeile 94: | ||
\cdot \sqrt{70\,\,{\rm MHz}}}\hspace{0.15cm}\underline{ \approx 3\,\,{\rm km}} | \cdot \sqrt{70\,\,{\rm MHz}}}\hspace{0.15cm}\underline{ \approx 3\,\,{\rm km}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
'''(2)''' Mit den Substitutionen | '''(2)''' Mit den Substitutionen | ||
:$$x = \frac{ t}{ T}, \hspace{0.2cm} K_1 = \frac{ {a}_{\rm \star}/T}{\sqrt{2 \pi^2 }}, \hspace{0.2cm} | :$$x = \frac{ t}{ T}, \hspace{0.2cm} K_1 = \frac{ {a}_{\rm \star}/T}{\sqrt{2 \pi^2 }}, \hspace{0.2cm} | ||
K_2 = \frac{ {a}_{\rm \star}^2}{2 \pi}$$ | K_2 = \frac{ {a}_{\rm \star}^2}{2 \pi}$$ | ||
| − | kann die Impulsantwort wie folgt beschrieben werden: | + | kann die Impulsantwort wie folgt beschrieben werden: |
| − | \hspace{0.05cm}.$ | + | :$$h_{\rm K}(x) = K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x} |
| − | Durch Nullsetzen der Ableitung folgt daraus: | + | \hspace{0.05cm}.$$ |
| + | *Durch Nullsetzen der Ableitung folgt daraus: | ||
:$$- {3}/{2} \cdot K_1 \cdot x^{-5/2}\cdot {\rm e}^{-K_2/x}+ K_1 \cdot x^{-3/2}\cdot {\rm | :$$- {3}/{2} \cdot K_1 \cdot x^{-5/2}\cdot {\rm e}^{-K_2/x}+ K_1 \cdot x^{-3/2}\cdot {\rm | ||
e}^{-K_2/x}\cdot (-K_2) \cdot (-x^{-2})= 0 | e}^{-K_2/x}\cdot (-K_2) \cdot (-x^{-2})= 0 | ||
| Zeile 107: | Zeile 109: | ||
x_{\rm max} = {2}/{3} \cdot K_2 = \frac{{a}_{\rm \star}^2}{3 \pi} | x_{\rm max} = {2}/{3} \cdot K_2 = \frac{{a}_{\rm \star}^2}{3 \pi} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Daraus ergibt sich für $60 \ \rm dB$ Kabeldämpfung ( | + | *Daraus ergibt sich für $60 \ \rm dB$ Kabeldämpfung $({a}_{\rm \star} \approx 6.9 \ \rm Np)$: |
:$$x_{\rm max} = { t_{\rm max}}/{ T}= { 6.9^2}/{(3\pi)}\hspace{0.15cm}\underline{ \approx 5 }\hspace{0.05cm}.$$ | :$$x_{\rm max} = { t_{\rm max}}/{ T}= { 6.9^2}/{(3\pi)}\hspace{0.15cm}\underline{ \approx 5 }\hspace{0.05cm}.$$ | ||
| − | '''(3)''' Setzt man das | + | '''(3)''' Setzt man das Ergebnis in die vorgegebene Gleichung ein, so erhält man (zur Vereinfachung verwenden wir „${a}$” anstelle von „${a}_{\rm \star}$”): |
:$$h_{\rm K}(t_{\rm max}) = \frac{1}{T} \cdot \frac{ {a}}{ \sqrt{2 \pi^2 \cdot {{a}^6}/{(3\pi)^3}}}\hspace{0.1cm} \cdot | :$$h_{\rm K}(t_{\rm max}) = \frac{1}{T} \cdot \frac{ {a}}{ \sqrt{2 \pi^2 \cdot {{a}^6}/{(3\pi)^3}}}\hspace{0.1cm} \cdot | ||
{\rm exp} \left[ - \frac{{a}^2}{2\pi} \cdot | {\rm exp} \left[ - \frac{{a}^2}{2\pi} \cdot | ||
| Zeile 119: | Zeile 121: | ||
}{2}} \cdot {\rm e}^{-3/2} \approx \frac{1}{T} \cdot \frac{1.453}{{a}^2} | }{2}} \cdot {\rm e}^{-3/2} \approx \frac{1}{T} \cdot \frac{1.453}{{a}^2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Mit $a = 6.9$ kommt man somit zum Endergebnis: | + | *Mit $a = 6.9$ kommt man somit zum Endergebnis: |
:$${\rm Max}\,[h_{\rm K}(t)] = \frac{1.453}{{6.9\,}^2} \cdot {1}/{T}\hspace{0.15cm}\underline{\approx 0.03 \cdot {1}/{T}} | :$${\rm Max}\,[h_{\rm K}(t)] = \frac{1.453}{{6.9\,}^2} \cdot {1}/{T}\hspace{0.15cm}\underline{\approx 0.03 \cdot {1}/{T}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | '''(4)''' Mit dem Ergebnis aus '''(3)''' lautet die geeignete Bestimmungsgleichung: | |
| − | '''(4)''' Mit dem Ergebnis aus (3) lautet die geeignete Bestimmungsgleichung: | ||
:$$\frac{ {a}/T}{ \sqrt{2 \pi^2 \cdot (t_{5\%}/T)^3}}= 0.05 \cdot 0.03 {1}/{T} | :$$\frac{ {a}/T}{ \sqrt{2 \pi^2 \cdot (t_{5\%}/T)^3}}= 0.05 \cdot 0.03 {1}/{T} | ||
\hspace{0.15cm}{= 0.0015 \cdot {1}/{T}} | \hspace{0.15cm}{= 0.0015 \cdot {1}/{T}} | ||
| − | \hspace{0. | + | \hspace{0.2cm} \Rightarrow \hspace{0.2cm} (t_{5\%}/T)^{3/2} = \frac{a}{\sqrt{2} \cdot \pi \cdot |
0.0015}\approx 1036 \hspace{0.3cm}\Rightarrow | 0.0015}\approx 1036 \hspace{0.3cm}\Rightarrow | ||
\hspace{0.3cm} | \hspace{0.3cm} | ||
\hspace{0.15cm}\underline{t_{5\%}/T \approx 103.5} \hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{t_{5\%}/T \approx 103.5} \hspace{0.05cm}.$$ | ||
| − | Dieser Wert ist etwas zu groß, da der zweite Term ${\rm e}^{-0.05}\approx 0.95$ vernachlässigt wurde. Die exakte Berechnung liefert $t_{\rm 5\%}/T \approx 97$. | + | *Dieser Wert ist etwas zu groß, da der zweite Term ${\rm e}^{-0.05}\approx 0.95$ vernachlässigt wurde. |
| + | *Die exakte Berechnung liefert $t_{\rm 5\%}/T \approx 97$. | ||
| − | '''(5)''' Richtig ist <u>der zweite Lösungsvorschlag</u>: | + | '''(5)''' Richtig ist <u>der zweite Lösungsvorschlag</u>: |
*Allgemein gilt: | *Allgemein gilt: | ||
:$$g_r(t) = g_s(t) \star h_{\rm K}(t) = s_0 \cdot | :$$g_r(t) = g_s(t) \star h_{\rm K}(t) = s_0 \cdot | ||
\int_{t-T/2}^{t+T/2} h_{\rm K}(\tau) \,{\rm d} \tau .$$ | \int_{t-T/2}^{t+T/2} h_{\rm K}(\tau) \,{\rm d} \tau .$$ | ||
| − | *Da sich die Kanalimpulsantwort $h_{\rm K}(t)$ innerhalb einer Symboldauer nur unwesentlich ändert, kann | + | *Da sich die Kanalimpulsantwort $h_{\rm K}(t)$ innerhalb einer Symboldauer nur unwesentlich ändert, kann näherungdweise auch geschrieben werden: |
:$$g_r(t) = h_{\rm K}(t) \cdot s_0 \cdot T.$$ | :$$g_r(t) = h_{\rm K}(t) \cdot s_0 \cdot T.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 12. November 2021, 18:35 Uhr
Der Frequenzgang eines Koaxialkabels der Länge $l$ ist durch folgende Formel darstellbar:
- $$H_{\rm K}(f) = {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} \cdot {\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
Der erste Term dieser Gleichung ist auf die Ohmschen Verluste zurückzuführen, der zweite Term auf die Querverluste. Dominant ist jedoch der Skineffekt, der durch den dritten Term ausgedrückt wird.
Mit den für ein „Normalkoaxialkabel” $\text{(2.6 mm}$ Kerndurchmesser, $\text{9.5 mm}$ Außendurchmesser$)$ gültigen Koeffizienten
- $$\alpha_2 = 0.2722 \hspace{0.15cm}\frac {\rm Np}{\rm km \cdot \sqrt{\rm MHz}} \hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722 \hspace{0.15cm}\frac {\rm rad}{\rm km \cdot \sqrt{\rm MHz}}\hspace{0.05cm}$$
lässt sich dieser Frequenzgang auch wie folgt darstellen:
- $$H_{\rm K}(f) \approx {\rm e}^{- 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}} } \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} \hspace{0.05cm}.$$
⇒ Dämpfungsverlauf ${a}_{\rm K}(f)$ und Phasenverlauf $b_{\rm K}(f)$ sind bis auf die Pseudoeinheiten „Np” bzw. „rad” identisch.
Definiert man die charakteristische Kabeldämpfung ${a}_{\rm *}$ bei der halben Bitrate $($also bei $R/2)$ und normiert die Frequenz auf $R$, so kann man Digitalsysteme unterschiedlicher Bitrate und Länge einheitlich behandeln:
- $${a}_{\rm \star} = {a}_{\rm K}(f ={R}/{2}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- {a}_{\rm \star} \cdot \sqrt{2f/R}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} {a}_{\star} \cdot \sqrt{2f/R}}\hspace{0.4cm}{\rm mit}\hspace{0.2cm}{a}_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} \hspace{0.05cm}.$$
- Der entsprechende $\rm dB$–Wert ist um den Faktor $8.686$ größer.
- Bei einem Binärsystem gilt $R = 1/T$, so dass sich die charakteristische Kabeldämpfung auf die Frequenz $f = 1/(2T)$ bezieht.
Die Fouriertransformierte von $H_{\rm K}(f)$ liefert die Impulsantwort $h_{\rm K}(t)$, die für ein Koaxialkabel mit den hier beschriebenen Näherungen in geschlossen–analytischer Form angebbar ist. Für ein Binärsystem gilt:
- $$h_{\rm K}(t) = \frac{ {a}_{\rm \star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot {\rm e}^{ - {{a}_{\rm \star}^2}/(2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm} t/T)} \hspace{0.4cm}{\rm mit}\hspace{0.2cm}{a}_{\rm \star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} \hspace{0.05cm}.$$
Die Teilaufgabe (5) bezieht sich auf den Empfangsgrundimpuls $g_r(t) = g_s(t) \star h_{\rm K}(t)$, wobei für $g_s(t)$ ein Rechteck mit Höhe $s_0$ und Dauer $T$ angenommen wird.
Hinweise:
- Die Aufgabe gehört zum Kapitel Eigenschaften von Koaxialkabeln.
- Sie können zur Überprüfung Ihrer Ergebnisse das interaktive SWF–Applet Zeitverhalten von Kupferkabeln benutzen.
Fragebogen
Musterlösung
- $$\alpha_2 \cdot l \cdot {R}/{2} = 6.9\,\,{\rm Np} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} l = \frac{6.9\,\,{\rm Np}}{0.2722 \,\, {\rm Np}/({\rm km \cdot \sqrt{\rm MHz}}) \cdot \sqrt{70\,\,{\rm MHz}}}\hspace{0.15cm}\underline{ \approx 3\,\,{\rm km}} \hspace{0.05cm}.$$
(2) Mit den Substitutionen
- $$x = \frac{ t}{ T}, \hspace{0.2cm} K_1 = \frac{ {a}_{\rm \star}/T}{\sqrt{2 \pi^2 }}, \hspace{0.2cm} K_2 = \frac{ {a}_{\rm \star}^2}{2 \pi}$$
kann die Impulsantwort wie folgt beschrieben werden:
- $$h_{\rm K}(x) = K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x} \hspace{0.05cm}.$$
- Durch Nullsetzen der Ableitung folgt daraus:
- $$- {3}/{2} \cdot K_1 \cdot x^{-5/2}\cdot {\rm e}^{-K_2/x}+ K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x}\cdot (-K_2) \cdot (-x^{-2})= 0 \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm} {3}/{2} \cdot x^{-5/2} = K_2 \cdot x^{-7/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x_{\rm max} = {2}/{3} \cdot K_2 = \frac{{a}_{\rm \star}^2}{3 \pi} \hspace{0.05cm}.$$
- Daraus ergibt sich für $60 \ \rm dB$ Kabeldämpfung $({a}_{\rm \star} \approx 6.9 \ \rm Np)$:
- $$x_{\rm max} = { t_{\rm max}}/{ T}= { 6.9^2}/{(3\pi)}\hspace{0.15cm}\underline{ \approx 5 }\hspace{0.05cm}.$$
(3) Setzt man das Ergebnis in die vorgegebene Gleichung ein, so erhält man (zur Vereinfachung verwenden wir „${a}$” anstelle von „${a}_{\rm \star}$”):
- $$h_{\rm K}(t_{\rm max}) = \frac{1}{T} \cdot \frac{ {a}}{ \sqrt{2 \pi^2 \cdot {{a}^6}/{(3\pi)^3}}}\hspace{0.1cm} \cdot {\rm exp} \left[ - \frac{{a}^2}{2\pi} \cdot \frac{3\pi}{{\rm a}^2}\hspace{0.1cm}\right] = \frac{1}{T} \cdot \frac{1}{{a}^2}\cdot \sqrt{\frac{27 \pi }{2}} \cdot {\rm e}^{-3/2} \approx \frac{1}{T} \cdot \frac{1.453}{{a}^2} \hspace{0.05cm}.$$
- Mit $a = 6.9$ kommt man somit zum Endergebnis:
- $${\rm Max}\,[h_{\rm K}(t)] = \frac{1.453}{{6.9\,}^2} \cdot {1}/{T}\hspace{0.15cm}\underline{\approx 0.03 \cdot {1}/{T}} \hspace{0.05cm}.$$
(4) Mit dem Ergebnis aus (3) lautet die geeignete Bestimmungsgleichung:
- $$\frac{ {a}/T}{ \sqrt{2 \pi^2 \cdot (t_{5\%}/T)^3}}= 0.05 \cdot 0.03 {1}/{T} \hspace{0.15cm}{= 0.0015 \cdot {1}/{T}} \hspace{0.2cm} \Rightarrow \hspace{0.2cm} (t_{5\%}/T)^{3/2} = \frac{a}{\sqrt{2} \cdot \pi \cdot 0.0015}\approx 1036 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{t_{5\%}/T \approx 103.5} \hspace{0.05cm}.$$
- Dieser Wert ist etwas zu groß, da der zweite Term ${\rm e}^{-0.05}\approx 0.95$ vernachlässigt wurde.
- Die exakte Berechnung liefert $t_{\rm 5\%}/T \approx 97$.
(5) Richtig ist der zweite Lösungsvorschlag:
- Allgemein gilt:
- $$g_r(t) = g_s(t) \star h_{\rm K}(t) = s_0 \cdot \int_{t-T/2}^{t+T/2} h_{\rm K}(\tau) \,{\rm d} \tau .$$
- Da sich die Kanalimpulsantwort $h_{\rm K}(t)$ innerhalb einer Symboldauer nur unwesentlich ändert, kann näherungdweise auch geschrieben werden:
- $$g_r(t) = h_{\rm K}(t) \cdot s_0 \cdot T.$$