Aufgaben:Aufgabe 4.5: 2D-Prüfungsauswertung: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID267__Sto_A_4_5.png|right|]] | + | [[Datei:P_ID267__Sto_A_4_5.png|right|Betrachtete Gaußsche 2D-WDF]] |
| − | + | In einer Studie wurden die Meisterprüfungen für das Handwerk untersucht, die sich stets aus einem theoretischen und zusätzlich einem praktischen Teil zusammensetzen. In der Grafik bezeichnet | |
| + | * $t$ die Punktzahl in der theoretischen Prüfung, | ||
| + | * $p$ die Punktzahl in der praktischen Prüfung. | ||
| − | + | Beide Zufallsgrößen ($t$ und $p$) sind dabei jeweils auf die Maximalpunktezahlen normiert und können deshalb nur Werte zwischen 0 und 1 annehmen. | |
| − | : | + | Beide Zufallsgrößen sind zudem als kontinuierliche Zufallsgrößen zu interpretieren, das heißt: $t$ und $p$ sind nicht auf diskrete Zahlenwerte beschränkt. |
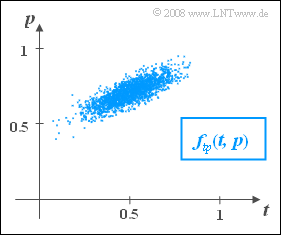
| − | + | Die Grafik zeigt die WDF $f_{tp}(t, p)$ der zweidimensionalen Zufallsgröße $(t, p)$, die nach der Auswertung von insgesamt $N = 10\hspace{0.05cm}000$ Abschlussarbeiten veröffentlicht wurde. Diese Funktion wurde mit Hilfe eines Auswertungsprogramms empirisch wie folgt angenähert: | |
| + | :$$f_{tp}(t,p) = \rm 13.263\cdot \rm exp \Bigg\{-\frac{(\it t - \rm 0.5)^{\rm 2}}{\rm 0.0288}-\frac{(\it p-\rm 0.7)^{\rm 2}}{\rm 0.0072} + \frac{(\it t-\rm 0.5)(\it p-\rm 0.7)}{\rm 0.0090}\Bigg\}.$$ | ||
| − | |||
| − | :Die | + | ''Hinweise:'' |
| − | : | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen|Zweidimensionale Zufallsgrößen]]. |
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Die hier behandelte Thematik ist in zwei Lernvideos zusammengefasst: | ||
| + | :[[Gaußsche Zufallsgrößen ohne statistische Bindungen]] | ||
| + | :[[Gaußsche Zufallsgrößen mit statistischen Bindungen]] | ||
| − | |||
| Zeile 23: | Zeile 28: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist der Mittelwert der im Theorieteil erzielten Ergebnisse? | + | {Wie groß ist der Mittelwert $m_t$ der im Theorieteil erzielten Ergebnisse? |
|type="{}"} | |type="{}"} | ||
| − | $m_t$ | + | $m_t \ = $ { 0.5 3% } |
| − | {Wie groß ist der Mittelwert der im Praxisteilteil erzielten Ergebnisse? Geben Sie auch die WDF der mittelwertfreien Zufallsgröße ( | + | {Wie groß ist der Mittelwert $m_p$ der im Praxisteilteil erzielten Ergebnisse? Geben Sie auch die WDF der mittelwertfreien Zufallsgröße $(t', p')$ an. |
|type="{}"} | |type="{}"} | ||
| − | $m_p$ | + | $m_p \ = $ { 0.7 3% } |
| − | {Berechnen Sie die Streuungen (Standardabweichungen) | + | {Berechnen Sie die Streuungen (Standardabweichungen) $\sigma_t$ und $\sigma_p$ sowie den Korrelationskoeffizienten $\rho$ zwischen den beiden Größen an. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_t$ | + | $\sigma_t \ = $ { 0.2 3% } |
| − | $\sigma_p$ | + | $\sigma_p \ = $ { 0.1 3% } |
| − | $\rho$ | + | $\rho \ = $ { 0.8 3% } |
| − | {Welche der | + | {Welche der folgenden Aussagen sind zutreffend? |
|type="[]"} | |type="[]"} | ||
+ Der Gauß-Ansatz ist für dieses Problem nur eine Näherung. | + Der Gauß-Ansatz ist für dieses Problem nur eine Näherung. | ||
| Zeile 46: | Zeile 51: | ||
| − | {Mit welcher Wahrscheinlichkeit hat ein Teilnehmer in der Theorie– und der Praxis–Prüfung jeweils zwischen 49% und 51% der Punkte erreicht? | + | {Mit welcher Wahrscheinlichkeit hat ein Teilnehmer in der Theorie– und der Praxis–Prüfung jeweils zwischen $49\%$ und $51\%$ der Punkte erreicht? |
|type="{}"} | |type="{}"} | ||
| − | $Pr[(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)]$ | + | ${\rm Pr}[(0.49 ≤ t ≤0.51)∩(0.49≤ p ≤0.51)]\ = $ { 2 3% } $\ \cdot 10^{-5}$ |
Version vom 20. März 2017, 14:57 Uhr
In einer Studie wurden die Meisterprüfungen für das Handwerk untersucht, die sich stets aus einem theoretischen und zusätzlich einem praktischen Teil zusammensetzen. In der Grafik bezeichnet
- $t$ die Punktzahl in der theoretischen Prüfung,
- $p$ die Punktzahl in der praktischen Prüfung.
Beide Zufallsgrößen ($t$ und $p$) sind dabei jeweils auf die Maximalpunktezahlen normiert und können deshalb nur Werte zwischen 0 und 1 annehmen.
Beide Zufallsgrößen sind zudem als kontinuierliche Zufallsgrößen zu interpretieren, das heißt: $t$ und $p$ sind nicht auf diskrete Zahlenwerte beschränkt.
Die Grafik zeigt die WDF $f_{tp}(t, p)$ der zweidimensionalen Zufallsgröße $(t, p)$, die nach der Auswertung von insgesamt $N = 10\hspace{0.05cm}000$ Abschlussarbeiten veröffentlicht wurde. Diese Funktion wurde mit Hilfe eines Auswertungsprogramms empirisch wie folgt angenähert:
- $$f_{tp}(t,p) = \rm 13.263\cdot \rm exp \Bigg\{-\frac{(\it t - \rm 0.5)^{\rm 2}}{\rm 0.0288}-\frac{(\it p-\rm 0.7)^{\rm 2}}{\rm 0.0072} + \frac{(\it t-\rm 0.5)(\it p-\rm 0.7)}{\rm 0.0090}\Bigg\}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die hier behandelte Thematik ist in zwei Lernvideos zusammengefasst:
- Gaußsche Zufallsgrößen ohne statistische Bindungen
- Gaußsche Zufallsgrößen mit statistischen Bindungen
Fragebogen
Musterlösung
- 1. und 2. Die Mittelwerte mt = 0.5 und mp = 0.7 können aus der Skizze abgeschätzt und aus der angegebenen Gleichung exakt ermittelt werden. Die 2D–WDF der mittelwertfreien Größe lautet:
- $$f_{\it t'p'}(\it t', \it p') = \rm 13.263\cdot \rm exp\Bigg (-\frac{\it t'^{\rm 2}}{\rm 0.0288} - \frac{\it p'^{\rm 2}}{\rm 0.0072}+\frac{\it t'\cdot p'}{\rm 0.0090}\Bigg ). $$
- Zur Vereinfachung wird im Folgenden auf den Apostroph zur Kennzeichnung mittelwertfreier Größen verzichtet. Sowohl t als auch p sind bis einschließlich Aufgabe (d) als mittelwertfrei zu verstehen.
- 3. Die allgemeine Gleichung einer mittelwertfreien 2D-Zufallsgröße lautet:
- $$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm 2\it \pi\sigma_{\it t}\sigma_{\it p}\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot $$
- $$\hspace{0.5cm}\cdot \hspace{0.1cm} \rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 2(\rm 1-\rho^{\rm 2})\sigma_{\it t}^{\rm 2}} \hspace{0.1cm}-\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2(\rm 1-\it\rho^{\rm 2})\sigma_{\it p}^{\rm 2}}\hspace{0.1cm}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{(\rm 1-\it \rho^{\rm 2})\sigma_{\it t}\cdot\sigma_{\it p}}\Bigg\}.$$
- Die Größen σt, σp und ρ lassen sich durch Koeffizientenvergleich ermitteln. Ein Vergleich der beiden ersten Terme im Exponenten zeigt, dass σt = 2 · σp gelten muss. Damit lautet die WDF:
- $$f_{\it tp}(\it t, \it p)=\frac{\rm 1}{\rm 4\it \pi\sigma_{\it p}^{\rm 2}\sqrt{\rm 1- \it\rho^{\rm 2}}}\hspace{0.1cm}\cdot $$
- $$\cdot\hspace{0.1cm}\rm exp\Bigg\{-\hspace{0.1cm}\frac{\it t^{\rm 2}}{\rm 8(\rm 1-\rho^{\rm 2})\sigma_{\it p}^{\rm 2}} -\hspace{0.1cm}\frac{\it p^{\rm 2}}{\rm 2(\rm 1-\it\rho^{\rm 2})\sigma_{\it p}^{\rm 2}}+\hspace{0.1cm}\frac{\rho\cdot \it t\cdot \it p}{\rm 2(\rm 1-\it \rho^{\rm 2})\cdot\sigma_{\it p}^{\rm 2}}\Bigg\}.$$
- Aus dem zweiten Term des Exponenten folgt:
- $$\rm 2\cdot(\rm 1-\it\rho^{\rm 2})\cdot\it\sigma_{\it p}^{\rm 2}=\rm 0.0072\hspace{0.5cm}\Rightarrow \hspace{0.5cm} \it \sigma_{\it p}^{\rm 2} = \frac{\rm 0.0036}{\it({\rm 1}-\rho^{\rm 2})}.$$
- Der Faktor K = 13.263 liefert nun das Ergebnis
- $$K = \frac{\sqrt{\rm 1-\it\rho^{\rm 2}}}{\rm 4\it\pi\cdot \rm 0.0036}=\rm 13.263 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sqrt{\rm 1-\it\rho^{\rm 2}}=\rm 0.6 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\hspace{0.15cm}\underline{ \rm \rho = \rm 0.8}.$$
- Daraus ergeben sich die beiden Streuungen zu σp = 0.1 und σt = 0.2. Zur Kontrolle kann der letzte Term des Exponenten verwendet werden:
- $$\frac{(\rm 1 - \it \rho^{\rm 2})\cdot\it\sigma_{\it t}\cdot\sigma_{\it p}}{\it \rho} = \rm \frac{0.36\cdot 0.1\cdot 0.2}{0.8} = \rm 0.009.$$
- Dies stimmt mit dem vorgegebenen Wert überein.
- 4. Der Lösungsvorschlag 1 ist richtig. Im Grunde genommen ist (t, p) keine echte Gaußsche Zufallsgröße, da beide Komponenten begrenzt sind. Die Wahrscheinlichkeiten für die Ereignisse t < 0, t > 1, p < 0 und p > 1 sind somit Null. Bei Gaußschen Größen mit den hier vorliegenden Mittelwerten und Streuungen ergeben sich jedoch
- $$\rm Pr(\it t < \rm 0) = \rm Pr(\it t > \rm 1) = \rm Q(2.5)\approx 6\cdot 10^{-3},$$
- $$\rm Pr(\it p > \rm 1) = \rm Q(3)\approx 1.3\cdot 10^{-3},$$
- $$\rm Pr(\it p < \rm 0) = \rm Q(7)\approx 10^{-12}.$$
- Der Korrelationskoeffizient ρ = 0.8 ist hier positiv. Hat der Prüfling im theoretischen Teil eher gut abgeschnitten, so ist (zumindest bei dieser Aufgabe) zu erwarten, dass auch der praktische Teil gut läuft. Hier ist der Lösungsvorschlag 2 somit falsch. In der Praxis ist das sicher nicht immer so.
- 5. Für diese Wahrscheinlichkeit gilt mit Δt = Δp = 0.02:
- $$\rm Pr\Bigg (( \rm 0.5-\frac{\rm\Delta\it t}{\rm 2}\le \it t \le \rm 0.5+\frac{\rm\Delta\it t}{\rm 2})\cap(\rm 0.5-\frac{\rm\Delta\it p}{\rm 2}\le \it p \le \rm 0.5+\frac{\rm\Delta\it p}{\rm 2})\Bigg)$$
- $$\approx \rm\Delta\it t\cdot\rm\Delta\it p\cdot \it f_{tp}(t=\rm 0.5, \it p = \rm 0.5).$$
- Für die 2D-WDF gilt unter Berücksichtigung der Mittelwerte mt = 0.5 und mp = 0.7:
- $$f_{tp}(\it t=\rm 0.5, \it p=\rm 0.5) = \rm 13.263\cdot exp(-\frac{(-0.2)^{2}}{0.0072})\approx 0.0513.$$
- Damit ergibt sich die gesuchte Wahrscheinlichkeit zu 0.02 · 0.02 · 0.0513 ≈ 2 · 10–5.