Aufgaben:Aufgabe 4.4Z: Ergänzung zur Aufgabe 4.4: Unterschied zwischen den Versionen
| (24 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Soft–in Soft–out Decoder}} | {{quiz-Header|Buchseite=Kanalcodierung/Soft–in Soft–out Decoder}} | ||
| − | [[Datei:P_ID2994__KC_Z_4_4_v3.png |right|frame| | + | [[Datei:P_ID2994__KC_Z_4_4_v3.png |right|frame|Hamming–Gewichte und Sequenzwahrscheinlichkeiten ]] |
| − | Der Informationstheoretiker [https:// | + | Der Informationstheoretiker [https://de.wikipedia.org/wiki/Robert_Gray_Gallager Robert G. Gallager] hat sich bereits 1963 mit folgender Fragestellung beschäftigt: |
| − | * Gegeben ist ein Zufallsvektor $\underline{x} = (x_1, \, x_2, \ ... \ | + | * Gegeben ist ein Zufallsvektor $\underline{x} = (x_1, \, x_2, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_n)$ mit $n$ binären Elementen $x_i ∈ \{0, \, 1\}$. |
| − | * Bekannt sind alle Wahrscheinlichkeiten $p_i = {\rm Pr}(x_i = 1)$ und $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ mit | + | * Bekannt sind alle Wahrscheinlichkeiten $p_i = {\rm Pr}(x_i = 1)$ und $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ mit Index $i = 1, \hspace{-0.04cm}\text{ ...} \hspace{0.08cm} ,\ n$. |
* Gesucht ist die Wahrscheinlichkeit, dass die Anzahl der Einsen in diesem Vektor geradzahlig ist. | * Gesucht ist die Wahrscheinlichkeit, dass die Anzahl der Einsen in diesem Vektor geradzahlig ist. | ||
| − | * Oder ausgedrückt mit dem [[Hamming–Gewicht]]: Wie groß ist die Wahrscheinlichkeit ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$? | + | * Oder ausgedrückt mit dem [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung|Hamming–Gewicht]]: Wie groß ist die Wahrscheinlichkeit ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$? |
| − | Die Grafik verdeutlicht die Aufgabenstellung für das Beispiel $n = 4$ sowie $p_1 = 0.2, | + | Die Grafik verdeutlicht die Aufgabenstellung für das Beispiel $n = 4$ sowie $p_1 = 0.2$, $p_2 = 0.9$, $p_3 = 0.3$ und $p_4 = 0.6$. |
| − | * Für die grün hinterlegte Zeile ⇒ $\underline{x} = (1, \, 0, \, 0, \, 1)$ gilt $w_{\rm H}(\underline{x}) = 2$ und ${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084$ | + | * Für die grün hinterlegte Zeile ⇒ $\underline{x} = (1, \, 0, \, 0, \, 1)$ gilt $w_{\rm H}(\underline{x}) = 2$ und |
| − | * Blaue Schrift bedeutet | + | :$${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084.$$ |
| − | * Die | + | * Blaue Schrift bedeutet „$w_{\rm H}(\underline{x})$ ist gerade”. Rote Schrift steht für „$w_{\rm H}(\underline{x})$ ist ungerade”. |
| + | * Die Wahrscheinlichkeit ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$ ist die Summe der blauen Zahlen in der letzten Spalte. | ||
| + | *Die Summe der roten Zahlen ergibt ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ ungerade}] = 1 - {\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$. | ||
Gallager hat das Problem in analytischer Weise gelöst: | Gallager hat das Problem in analytischer Weise gelöst: | ||
| − | :$$ | + | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \right ] |
\hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 + \pi]\hspace{0.05cm},$$ | \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 + \pi]\hspace{0.05cm},$$ | ||
:$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} | ||
\right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 - \pi]\hspace{0.05cm}.$$ | \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 - \pi]\hspace{0.05cm}.$$ | ||
| + | |||
| + | Hierbei ist die folgende Hilfsgröße verwendet: | ||
| + | :$$\pi = \prod\limits_{i =1}^{n} \hspace{0.25cm}(1-2p_i) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Gleichung wendet man zum Beispiel an, um die extrinsischen $L$–Werte eines <i>Single Parity–check Codes</i> zu berechnen. | ||
| + | |||
| + | Wie bereits in der [[Aufgaben:4.4_Extrinsische_L%E2%80%93Werte_beim_SPC| Aufgabe A4.4]] dargelegt, lautet nämlich der extrinsische $L$–Wert mit dem Hamming–Gewicht $w_{\rm H}$ der verkürzten Folge $\underline{x}^{(-i)}$: | ||
| + | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Hierbei ist berücksichtigt, dass man für $L_{\rm E}(i)$ nur die anderen Symbole $(j ≠ i)$ heranziehen darf: | ||
| + | :$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Soft%E2%80%93in_Soft%E2%80%93out_Decoder| Soft–in Soft–out Decoder]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Kanalcodierung/Soft–in_Soft–out_Decoder#Zur_Berechnung_der_extrinsischen_L.E2.80.93Werte|Zur Berechnung der extrinsischen $L$–Werte]]. | ||
| + | *Die Aufgabe ist als Ergänzung zur [[Aufgaben:Aufgabe_4.4:_Extrinsische_L–Werte_beim_SPC| Aufgabe 4.4]] gedacht. | ||
| + | |||
| Zeile 25: | Zeile 54: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wir betrachten den Vektor $\underline{x} = (x_1, \, x_2) \ \Rightarrow \ n = 2$ mit $x_i ∈ \{0, \, 1\}$. Wie groß ist die Wahrscheinlichkeit, dass $\underline{x}$ eine gerade Anzahl an Einsen beinhaltet? | + | {Wir betrachten den Vektor $\underline{x} = (x_1, \, x_2) \ \Rightarrow \ n = 2$ mit $x_i ∈ \{0, \, 1\}$ und $p_1 = 0.2, \ p_2 = 0.9$. <br>Wie groß ist die Wahrscheinlichkeit, dass $\underline{x}$ eine gerade Anzahl an Einsen beinhaltet? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}\big [w_{\rm H}(\underline{x}) \ {\rm ist \ gerade}\big ] \ = \ ${ 0.26 3% } |
| − | {Berechnen Sie die gleiche Wahrscheinlichkeit für $\underline{x} = (x_1, \, x_2, \, x_3) \ \Rightarrow \ n = 3$. | + | {Berechnen Sie die gleiche Wahrscheinlichkeit für $\underline{x} = (x_1, \, x_2, \, x_3) \ \Rightarrow \ n = 3$ und $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}\big [w_{\rm H}(\underline{x}) \ {\rm ist \ gerade}\big ] \ = \ ${ 0.404 3% } |
| − | {Nun gelte $n = 4$ und $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6$. Berechnen Sie nach der Gallager–Gleichung folgende Größen: | + | {Nun gelte $n = 4$ und $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6$. Berechnen Sie nach der Gallager–Gleichung folgende Größen: |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr(blau) = Pr}[w_{\rm H}(\underline{x}) {\rm ist \ gerade}] \ = \ ${ 0.5192 3% } | + | ${\rm Pr(blau) = Pr}\big [w_{\rm H}(\underline{x}) \ {\rm ist \ gerade}\big ] \hspace{0.33cm} = \ ${ 0.5192 3% } |
| − | ${\rm Pr(rot) = Pr}[w_{\rm H}(\underline{x}) {\rm ist \ ungerade}] \ = \ ${ 0.4808 3% } | + | ${\rm Pr(rot) = Pr}\big [w_{\rm H}(\underline{x}) \ {\rm ist \ ungerade}\big ] \hspace{0.1cm} = \ ${ 0.4808 3% } |
| − | $Q = {\rm Pr(blau)/Pr(rot)} \ = \ ${ 1.0799 3% } | + | $\text{Quotient }Q = {\rm Pr(blau)/Pr(rot)} \hspace{0.4cm} = \ ${ 1.0799 3% } |
| − | {Wie groß ist der extrinsische $L$–Wert für das Symbol $i = 5$ beim SPC (5, 4, 2) mit $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6, \ p_5 = 0.9$? | + | {Wie groß ist der extrinsische $L$–Wert für das Symbol $i = 5$ beim $\text{SPC (5, 4, 2)}$ mit $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6, \ p_5 = 0.9$? |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(i = 5) \ = \ ${ 0.077 3% } | $L_{\rm E}(i = 5) \ = \ ${ 0.077 3% } | ||
| − | {Wie | + | {Wie ändert sich $L_{\rm E}(i = 5)$, wenn man stattdessen von $p_5 = 0.1$ ausgeht? |
| − | |type=" | + | |type="()"} |
| − | - $L_{\rm E}(i = 5)$ wird größer. | + | - $L_{\rm E}(i = 5)$ wird größer. |
| − | - $L_{\rm E}(i = 5)$ wird kleiner. | + | - $L_{\rm E}(i = 5)$ wird kleiner. |
| − | + $L_{\rm E}(i = 5)$ wird gegenüber Teilaufgabe (4) nicht verändert. | + | + $L_{\rm E}(i = 5)$ wird gegenüber Teilaufgabe '''(4)''' nicht verändert. |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | [[Datei:P_ID2996__KC_Z_4_4a_v1.png|frame|right|Herleitung „$w_{\rm H}$ ist gerade” für die Codelänge $n = 2$]] | |
| + | '''(1)''' Entsprechend der nebenstehenden Tabelle gilt: | ||
:$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.10cm}{\rm ist \hspace{0.10cm} gerade}\right ] = | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.10cm}{\rm ist \hspace{0.10cm} gerade}\right ] = | ||
{\rm Pr} \left [w_{\rm H} = 0 \right] + {\rm Pr} \left [w_{\rm H} = 2 \right] | {\rm Pr} \left [w_{\rm H} = 0 \right] + {\rm Pr} \left [w_{\rm H} = 2 \right] | ||
| Zeile 71: | Zeile 101: | ||
Die Gallager–Gleichung liefert für den gleichen Parametersatz: | Die Gallager–Gleichung liefert für den gleichen Parametersatz: | ||
| − | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{2} \hspace{0.25cm}(1-2\cdot p_i) = | + | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{2} \hspace{0.25cm}(1-2\cdot p_i) = 0.5 + 0.5 \cdot (1 - 2 \cdot 0.2)\cdot (1 - 2 \cdot 0.9) = 0.26 |
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 78: | Zeile 107: | ||
| − | + | [[Datei:P_ID2997__KC_Z_4_4b_v1.png|right|frame|Herleitung „$w_{\rm H}$ ist gerade” für die Codelänge $n = 3$]] | |
| − | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] = 0.056 | + | '''(2)''' In der zweiten Tabelle sind die vier Kombinationen mit einer geraden Anzahl an Einsen blau markiert. Die Auftrittswahrscheinlichkeiten der einzelnen Kombinationen sind in der letzten Spalte angegeben. Somit ergibt sich: |
| − | + | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] = 0.056 + 0.216 + 0.006 + 0.126 \hspace{0.15cm} \underline{= 0.404} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Die roten Zeilen liefern das Komplementärereignis: | Die roten Zeilen liefern das Komplementärereignis: | ||
| − | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right] = 0.024 | + | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right] = 0.024 + 0.504 + 0.014 + 0.054= 0.596 |
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die Gallager–Gleichung liefert auch hier wieder das exakt gleiche Ergebnis | + | Die Gallager–Gleichung liefert auch hier wieder das exakt gleiche Ergebnis, wobei anzumerken ist, dass diese Gleichung für alle $n$ und alle beliebigen Wahrscheinlichkeiten gültig ist: |
| − | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{3} \hspace{0.25cm}(1-2\cdot p_i) | + | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{3} \hspace{0.25cm}(1-2\cdot p_i) $$ |
| − | :$$\ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot (+0.6) \cdot (-0.8) \cdot (+0.4) = 0.404 | + | :$$\Rightarrow\hspace{0.3cm}{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot (+0.6) \cdot (-0.8) \cdot (+0.4) = 0.404 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
'''(3)''' Entsprechend der Angabenseite gilt: | '''(3)''' Entsprechend der Angabenseite gilt: | ||
| − | :$$\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1 - 2 \cdot 0.2) \cdot (1 - 2 \cdot 0.9) \cdot (1 - 2 \cdot 0.3) \cdot (1 - 2 \cdot 0.6) | + | :$$\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1 - 2 \cdot 0.2) \cdot (1 - 2 \cdot 0.9) \cdot (1 - 2 \cdot 0.3) \cdot (1 - 2 \cdot 0.6) $$ |
| − | :$$\ = \ \hspace{-0.15cm} (+0.6) \cdot (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.0384 | + | :$$\Rightarrow\hspace{0.3cm}\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(+0.6) \cdot (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.0384 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 105: | Zeile 131: | ||
:$${\rm Pr}({\rm rot}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 - 0.5 \cdot \pi = 0.5 - 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.4808}\hspace{0.05cm}. $$ | :$${\rm Pr}({\rm rot}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 - 0.5 \cdot \pi = 0.5 - 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.4808}\hspace{0.05cm}. $$ | ||
| − | Addiert man die blauen bzw. die roten Wahrscheinlichkeiten auf der Angabenseite, so erhält man exakt die hier berechneten Werte. Für den Quotienten ergibt sich: | + | Addiert man die blauen bzw. die roten Wahrscheinlichkeiten auf der Angabenseite, so erhält man exakt die hier berechneten Werte. |
| + | |||
| + | Für den Quotienten ergibt sich: | ||
:$$Q = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right]} { {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right]} = \frac{0.5192}{0.4808}\hspace{0.15cm} \underline{= 1.0799} | :$$Q = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right]} { {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right]} = \frac{0.5192}{0.4808}\hspace{0.15cm} \underline{= 1.0799} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| Zeile 118: | Zeile 146: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Beim SPC (5, 4, 2) ⇒ $n = 5$ ergibt sich dieses Produkt für $i = 5$ aus folgenden vier Multiplikanden: | + | Beim $\text{SPC (5, 4, 2}$) ⇒ $n = 5$ ergibt sich dieses Produkt für $i = 5$ aus folgenden vier Multiplikanden: |
:$$\pi = \prod\limits_{j = 1, \hspace{0.05cm}2, \hspace{0.05cm}3, \hspace{0.05cm}4} \hspace{0.05cm}(1-2\cdot p_j) = | :$$\pi = \prod\limits_{j = 1, \hspace{0.05cm}2, \hspace{0.05cm}3, \hspace{0.05cm}4} \hspace{0.05cm}(1-2\cdot p_j) = | ||
(1-2\cdot p_1) \cdot (1-2\cdot p_2) \cdot (1-2\cdot p_3) \cdot (1-2\cdot p_4) | (1-2\cdot p_1) \cdot (1-2\cdot p_2) \cdot (1-2\cdot p_3) \cdot (1-2\cdot p_4) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Der Vergleich mit der Teilaufgabe (3) zeigt, dass $L_{\rm E}(i = 5) = \ln {Q} = \ln {(1.0799)} \underline{\approx 0.077}$ ist. | + | Der Vergleich mit der Teilaufgabe '''(3)''' zeigt, dass $L_{\rm E}(i = 5) = \ln {Q} = \ln {(1.0799)} \ \underline{\approx 0.077}$ ist. |
Aktuelle Version vom 5. Juli 2019, 14:48 Uhr
Der Informationstheoretiker Robert G. Gallager hat sich bereits 1963 mit folgender Fragestellung beschäftigt:
- Gegeben ist ein Zufallsvektor $\underline{x} = (x_1, \, x_2, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_n)$ mit $n$ binären Elementen $x_i ∈ \{0, \, 1\}$.
- Bekannt sind alle Wahrscheinlichkeiten $p_i = {\rm Pr}(x_i = 1)$ und $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ mit Index $i = 1, \hspace{-0.04cm}\text{ ...} \hspace{0.08cm} ,\ n$.
- Gesucht ist die Wahrscheinlichkeit, dass die Anzahl der Einsen in diesem Vektor geradzahlig ist.
- Oder ausgedrückt mit dem Hamming–Gewicht: Wie groß ist die Wahrscheinlichkeit ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$?
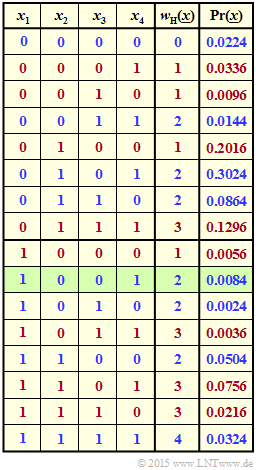
Die Grafik verdeutlicht die Aufgabenstellung für das Beispiel $n = 4$ sowie $p_1 = 0.2$, $p_2 = 0.9$, $p_3 = 0.3$ und $p_4 = 0.6$.
- Für die grün hinterlegte Zeile ⇒ $\underline{x} = (1, \, 0, \, 0, \, 1)$ gilt $w_{\rm H}(\underline{x}) = 2$ und
- $${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084.$$
- Blaue Schrift bedeutet „$w_{\rm H}(\underline{x})$ ist gerade”. Rote Schrift steht für „$w_{\rm H}(\underline{x})$ ist ungerade”.
- Die Wahrscheinlichkeit ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$ ist die Summe der blauen Zahlen in der letzten Spalte.
- Die Summe der roten Zahlen ergibt ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ ungerade}] = 1 - {\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ ist \ gerade}]$.
Gallager hat das Problem in analytischer Weise gelöst:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 + \pi]\hspace{0.05cm},$$
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 - \pi]\hspace{0.05cm}.$$
Hierbei ist die folgende Hilfsgröße verwendet:
- $$\pi = \prod\limits_{i =1}^{n} \hspace{0.25cm}(1-2p_i) \hspace{0.05cm}.$$
Die Gleichung wendet man zum Beispiel an, um die extrinsischen $L$–Werte eines Single Parity–check Codes zu berechnen.
Wie bereits in der Aufgabe A4.4 dargelegt, lautet nämlich der extrinsische $L$–Wert mit dem Hamming–Gewicht $w_{\rm H}$ der verkürzten Folge $\underline{x}^{(-i)}$:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass man für $L_{\rm E}(i)$ nur die anderen Symbole $(j ≠ i)$ heranziehen darf:
- $$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$
Hinweise:
- Die Aufgabe gehört zum Kapitel Soft–in Soft–out Decoder.
- Bezug genommen wird insbesondere auf die Seite Zur Berechnung der extrinsischen $L$–Werte.
- Die Aufgabe ist als Ergänzung zur Aufgabe 4.4 gedacht.
Fragebogen
Musterlösung
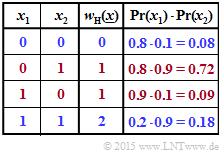
(1) Entsprechend der nebenstehenden Tabelle gilt:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.10cm}{\rm ist \hspace{0.10cm} gerade}\right ] = {\rm Pr} \left [w_{\rm H} = 0 \right] + {\rm Pr} \left [w_{\rm H} = 2 \right] \hspace{0.05cm}. $$
Mit den Wahrscheinlichkeiten
- $$p_1 = {\rm Pr} (x_1 = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.2\hspace{0.05cm},\hspace{0.3cm}q_1 = {\rm Pr} (x_1 = 0) = 0.8\hspace{0.05cm},$$
- $$p_2 = {\rm Pr} (x_2 = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.9\hspace{0.05cm},\hspace{0.3cm}q_2 = {\rm Pr} (x_2 = 0) = 0.1$$
erhält man:
- $${\rm Pr} \left [w_{\rm H}(\underline{x}) = 0\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr} \left [(x_1 = 0)\cap (x_2 = 0) \right] = q_1 \cdot q_2 = 0.8 \cdot 0.1 = 0.08 \hspace{0.05cm},$$
- $${\rm Pr} \left [w_{\rm H}(\underline{x}) = 2\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr} \left [(x_1 = 1)\cap (x_2 = 1) \right] = p_1 \cdot p_2 = 0.2 \cdot 0.9 = 0.18$$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] = 0.8 + 0.18 \hspace{0.15cm} \underline{= 0.26} \hspace{0.05cm}.$$
Die Gallager–Gleichung liefert für den gleichen Parametersatz:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{2} \hspace{0.25cm}(1-2\cdot p_i) = 0.5 + 0.5 \cdot (1 - 2 \cdot 0.2)\cdot (1 - 2 \cdot 0.9) = 0.26 \hspace{0.05cm}.$$
Die von Gallager 1963 angegebene Gleichung wurde hiermit für $n = 2$ verifiziert.
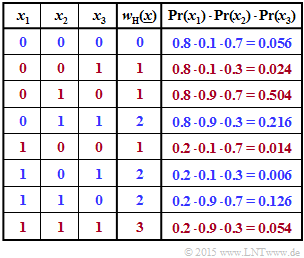
(2) In der zweiten Tabelle sind die vier Kombinationen mit einer geraden Anzahl an Einsen blau markiert. Die Auftrittswahrscheinlichkeiten der einzelnen Kombinationen sind in der letzten Spalte angegeben. Somit ergibt sich:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] = 0.056 + 0.216 + 0.006 + 0.126 \hspace{0.15cm} \underline{= 0.404} \hspace{0.05cm}.$$
Die roten Zeilen liefern das Komplementärereignis:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right] = 0.024 + 0.504 + 0.014 + 0.054= 0.596 \hspace{0.05cm}.$$
Die Gallager–Gleichung liefert auch hier wieder das exakt gleiche Ergebnis, wobei anzumerken ist, dass diese Gleichung für alle $n$ und alle beliebigen Wahrscheinlichkeiten gültig ist:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{3} \hspace{0.25cm}(1-2\cdot p_i) $$
- $$\Rightarrow\hspace{0.3cm}{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot (+0.6) \cdot (-0.8) \cdot (+0.4) = 0.404 \hspace{0.05cm}.$$
(3) Entsprechend der Angabenseite gilt:
- $$\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1 - 2 \cdot 0.2) \cdot (1 - 2 \cdot 0.9) \cdot (1 - 2 \cdot 0.3) \cdot (1 - 2 \cdot 0.6) $$
- $$\Rightarrow\hspace{0.3cm}\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(+0.6) \cdot (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.0384 \hspace{0.05cm}.$$
Daraus lassen sich berechnen:
- $${\rm Pr}({\rm blau}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \pi = 0.5 + 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.5192}\hspace{0.05cm},$$
- $${\rm Pr}({\rm rot}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 - 0.5 \cdot \pi = 0.5 - 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.4808}\hspace{0.05cm}. $$
Addiert man die blauen bzw. die roten Wahrscheinlichkeiten auf der Angabenseite, so erhält man exakt die hier berechneten Werte.
Für den Quotienten ergibt sich:
- $$Q = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade}\right]} { {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}\right]} = \frac{0.5192}{0.4808}\hspace{0.15cm} \underline{= 1.0799} \hspace{0.05cm}. $$
(4) Für den Single Parity–check Code wurde der extrinsische $L$–Wert bezüglich des $i$–ten Bits wie folgt angegeben:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm},$$
oder:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{1+\prod_{j \ne i} \hspace{0.25cm}(1-2\cdot p_j)}{1-\prod_{j \ne i} \hspace{0.25cm}(1-2\cdot p_j)} \hspace{0.05cm}.$$
Beim $\text{SPC (5, 4, 2}$) ⇒ $n = 5$ ergibt sich dieses Produkt für $i = 5$ aus folgenden vier Multiplikanden:
- $$\pi = \prod\limits_{j = 1, \hspace{0.05cm}2, \hspace{0.05cm}3, \hspace{0.05cm}4} \hspace{0.05cm}(1-2\cdot p_j) = (1-2\cdot p_1) \cdot (1-2\cdot p_2) \cdot (1-2\cdot p_3) \cdot (1-2\cdot p_4) \hspace{0.05cm}.$$
Der Vergleich mit der Teilaufgabe (3) zeigt, dass $L_{\rm E}(i = 5) = \ln {Q} = \ln {(1.0799)} \ \underline{\approx 0.077}$ ist.
(5) Richtig ist der Lösungsvorschlag 3, weil das Ergebnis für $L_{\rm E}(i = 5)$ unabhängig von $p_5$ ist.