Aufgaben:Aufgabe 4.2: Wieder Dreieckgebiet: Unterschied zwischen den Versionen
| Zeile 4: | Zeile 4: | ||
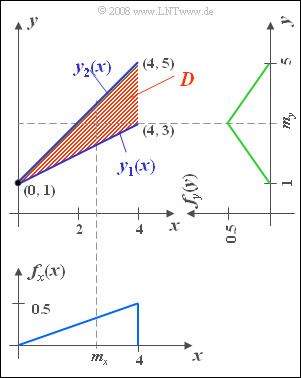
[[Datei:P_ID226__Sto_A_4_2.png|right|frame|Dreieckiges 2D-Gebiet und die beiden Randwahrscheinlichkeitsdichten]] | [[Datei:P_ID226__Sto_A_4_2.png|right|frame|Dreieckiges 2D-Gebiet und die beiden Randwahrscheinlichkeitsdichten]] | ||
| − | Wir betrachten die gleiche Zufallsgröße ( | + | Wir betrachten die gleiche Zufallsgröße $(x, \ y)$ wie in der [[Aufgaben:4.1_Dreieckiges_(x,_y)-Gebiet|Aufgabe 4.1]]: |
| − | *In einem durch die Eckpunkte $(0,\ 1)$, $(4,\ 3)$ und $(4,\ 5)$ definierten Gebiet $D$ sei die 2D–WDF $f_{xy} (x, y) = 0.25$. | + | *In einem durch die Eckpunkte $(0,\ 1)$, $(4,\ 3)$ und $(4,\ 5)$ definierten Gebiet $D$ sei die 2D–WDF $f_{xy} (x, y) = 0.25$. |
| − | *Außerhalb dieses in der Grafik rot markierten Definitionsgebietes $D$ gibt es keine Werte. | + | *Außerhalb dieses in der Grafik rot markierten Definitionsgebietes $D$ gibt es keine Werte. |
| − | Weiterhin sind in der Grafik die beiden Randwahrscheinlichkeitsdichten bezüglich den Größen $x$ und $y$ eingezeichnet, die bereits in der | + | Weiterhin sind in der Grafik die beiden Randwahrscheinlichkeitsdichten bezüglich den Größen $x$ und $y$ eingezeichnet, die bereits in der Aufgabe 4.1 ermittelt wurden. |
| − | Daraus lassen sich mit den Gleichungen des Kapitels [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente|Erwartungswerte und Momente]] die Kenngrößen der beiden Zufallsgrößen bestimmen: | + | Daraus lassen sich mit den Gleichungen des Kapitels [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente|Erwartungswerte und Momente]] die Kenngrößen der beiden Zufallsgrößen bestimmen: |
:$$m_x=8/3 ,\hspace{0.5cm} \sigma_x=\sqrt{8/9},$$ | :$$m_x=8/3 ,\hspace{0.5cm} \sigma_x=\sqrt{8/9},$$ | ||
:$$ m_y= 3,\hspace{0.95cm} \sigma_y = \sqrt{\rm 2/3}.$$ | :$$ m_y= 3,\hspace{0.95cm} \sigma_y = \sqrt{\rm 2/3}.$$ | ||
| − | Aufgrund der Tatsache, dass das Definitionsgebiet $D$ durch zwei Gerade $y_1(x)$ und $y_2(x)$ begrenzt ist, kann hier das gemeinsame Moment erster Ordnung wie folgt berechnet werden. | + | Aufgrund der Tatsache, dass das Definitionsgebiet $D$ durch zwei Gerade $y_1(x)$ und $y_2(x)$ begrenzt ist, kann hier das gemeinsame Moment erster Ordnung wie folgt berechnet werden. |
:$$m_{xy}={\rm E}\big[x\cdot y\big]=\int_{x_{1}}^{x_{2}}x\cdot \int_{y_{1}(x)}^{y_{2}(x)}y \cdot f_{xy}(x,y) \, \,{\rm d}y\, {\rm d}x.$$ | :$$m_{xy}={\rm E}\big[x\cdot y\big]=\int_{x_{1}}^{x_{2}}x\cdot \int_{y_{1}(x)}^{y_{2}(x)}y \cdot f_{xy}(x,y) \, \,{\rm d}y\, {\rm d}x.$$ | ||
| + | |||
| + | |||
| + | |||
| Zeile 23: | Zeile 26: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen|Zweidimensionale Zufallsgrößen]]. | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen|Zweidimensionale Zufallsgrößen]]. |
| − | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente|Erwartungswerte und Momente]]. | + | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente|Erwartungswerte und Momente]]. |
| Zeile 32: | Zeile 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lauten die Grenzgeraden des inneren Integrals zur $m_{xy}$–Berechnung? | + | {Wie lauten die Grenzgeraden des inneren Integrals zur $m_{xy}$–Berechnung? |
|type="()"} | |type="()"} | ||
- $y_1(x) = x+1, $ $y_2(x) = 2x+1.$ | - $y_1(x) = x+1, $ $y_2(x) = 2x+1.$ | ||
| Zeile 39: | Zeile 42: | ||
| − | {Berechnen Sie das gemeinsame Moment $m_{xy}$ gemäß dem Doppelintegral auf der Angabenseite. | + | {Berechnen Sie das gemeinsame Moment $m_{xy}$ gemäß dem Doppelintegral auf der Angabenseite. <i>Hinweis</i>: Setzen Sie $x_1 = 0$ und $x_2 = 4$. |
|type="{}"} | |type="{}"} | ||
$m_{xy} \ = \ $ { 8.667 3% } | $m_{xy} \ = \ $ { 8.667 3% } | ||
| − | {Welcher Wert ergibt sich für die Kovarianz $\mu_{xy}$ ? | + | {Welcher Wert ergibt sich für die Kovarianz $\mu_{xy}$ ? |
|type="{}"} | |type="{}"} | ||
$\mu_{xy}\ = \ $ { 0.667 3% } | $\mu_{xy}\ = \ $ { 0.667 3% } | ||
| − | {Wie groß ist der Korrelationskoeffizient $\rho_{xy}$? | + | {Wie groß ist der Korrelationskoeffizient $\rho_{xy}$? |
|type="{}"} | |type="{}"} | ||
$\rho_{xy}\ = \ $ { 0.866 3% } | $\rho_{xy}\ = \ $ { 0.866 3% } | ||
| − | {Wie lautet die Gleichung der Korrelationsgeraden $y = K(x)$? An welcher Stelle $y_0$ schneidet die Gerade die $y$-Achse? <br>Zeigen Sie, dass die Korrelationsgerade auch durch den Punkt $(m_x, m_y)$ geht. | + | {Wie lautet die Gleichung der Korrelationsgeraden $y = K(x)$ ? An welcher Stelle $y_0$ schneidet die Gerade die $y$-Achse? <br>Zeigen Sie, dass die Korrelationsgerade auch durch den Punkt $(m_x, m_y)$ geht. |
|type="{}"} | |type="{}"} | ||
$y_0\ = \ $ { 1 3% } | $y_0\ = \ $ { 1 3% } | ||
Version vom 26. November 2019, 13:35 Uhr
Wir betrachten die gleiche Zufallsgröße $(x, \ y)$ wie in der Aufgabe 4.1:
- In einem durch die Eckpunkte $(0,\ 1)$, $(4,\ 3)$ und $(4,\ 5)$ definierten Gebiet $D$ sei die 2D–WDF $f_{xy} (x, y) = 0.25$.
- Außerhalb dieses in der Grafik rot markierten Definitionsgebietes $D$ gibt es keine Werte.
Weiterhin sind in der Grafik die beiden Randwahrscheinlichkeitsdichten bezüglich den Größen $x$ und $y$ eingezeichnet, die bereits in der Aufgabe 4.1 ermittelt wurden.
Daraus lassen sich mit den Gleichungen des Kapitels Erwartungswerte und Momente die Kenngrößen der beiden Zufallsgrößen bestimmen:
- $$m_x=8/3 ,\hspace{0.5cm} \sigma_x=\sqrt{8/9},$$
- $$ m_y= 3,\hspace{0.95cm} \sigma_y = \sqrt{\rm 2/3}.$$
Aufgrund der Tatsache, dass das Definitionsgebiet $D$ durch zwei Gerade $y_1(x)$ und $y_2(x)$ begrenzt ist, kann hier das gemeinsame Moment erster Ordnung wie folgt berechnet werden.
- $$m_{xy}={\rm E}\big[x\cdot y\big]=\int_{x_{1}}^{x_{2}}x\cdot \int_{y_{1}(x)}^{y_{2}(x)}y \cdot f_{xy}(x,y) \, \,{\rm d}y\, {\rm d}x.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.
- Bezug genommen wird auch auf das Kapitel Erwartungswerte und Momente.
Fragebogen
Musterlösung
- Sowohl $y_1(x)$ als auch $y_2(x)$ schneiden die $y$-Achse bei $y= 1$.
- Die untere Begrenzungslinie hat die Steigung $0.5$, die obere die Steigung $1$.
(2) Entsprechend den Hinweisen erhalten wir:
- $$m_{xy}=\int_{\rm 0}^{\rm 4} x \cdot \int_{\it x/\rm 2 +\rm 1}^{\it x+\rm 1} {1}/{4}\cdot y \, \,{\rm d}y\,\, \, {\rm d}x = {1}/{8}\cdot \int_{\rm 0}^{\rm 4} x\cdot \big[( x+ 1)^{\rm 2}- ({ x}/{2}+1)^{\rm 2} \big] \,\, {\rm d}x.$$
Dies führt zum Integral bzw. Endergebnis:
- $$m_{xy}={1}/{8}\int_{\rm 0}^{\rm 4}(\frac{3}{4}\cdot x^{3}{\rm +} x^2\,{\rm d}x = \rm \frac{1}{8} \cdot (\frac{3}{16}\cdot 4^4+\rm \frac{4^3}{3})=\frac{26}{3}\hspace{0.15cm}\underline{ \approx 8.667}.$$
(3) Da beide Zufallsgrößen jeweils einen Mittelwert ungleich $0$ besitzen, folgt für die Kovarianz:
- $$\it \mu_{xy}=\it m_{xy}-m_{x}\cdot m_{y}=\frac{\rm 26}{\rm 3}-\frac{\rm 8}{\rm 3}\cdot\rm 3={2}/{3} \hspace{0.15cm}\underline{=0.667}.$$
(4) Mit den angegebenen Streuungen erhält man:
- $$\rho_{xy}=\frac{\mu_{xy}}{\sigma_{x}\cdot\sigma_{y}}=\frac{{\rm 2}/{\rm 3}}{\sqrt{{\rm 8}/{\rm 9}}\cdot\sqrt{{\rm 2}/{\rm 3}}}=\sqrt{0.75}\hspace{0.15cm}\underline{=\rm 0.866}.$$
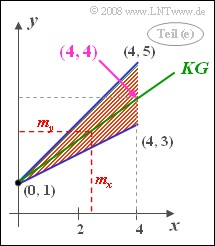
(5) Für die Korrelationsgerade (KG) gilt allgemein:
- $$ y-m_{y}=\rho_{xy}\cdot\frac{\sigma_{y}}{\sigma_ {x}}\cdot(x-m_{x}).$$
Mit den oben berechneten Zahlenwerten erhält man
- $$y={\rm 3}/{\rm 4}\cdot x +\rm 1.$$
Die Korrelationsgerade schneidet die $y$-Achse bei $\underline{y=1}$ und geht auch durch den Punkt $(4, 4)$. Jedes andere Ergebnis wäre auch nicht zu interpretieren, wenn man das Definitionsgebiet betrachtet:
- Setzt man $m_x = 8/3$ ein, so erhält man $y = m_y = 3$.
- Das heißt: Die berechnete Korrelationsgerade geht tatsächlich durch den Punkt $(m_x, m_y)$, wie es die Theorie besagt.