Aufgabe 4.1: Dreieckiges (x, y)-Gebiet
Aus LNTwww
Version vom 13. September 2016, 17:59 Uhr von Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Zweidimensionale Zufallsgrößen }} right| :Eine 2D-Zufallsgrö&szli…“)
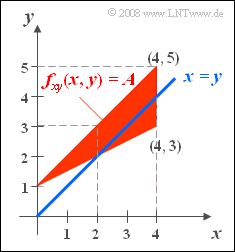
- Eine 2D-Zufallsgröße ist durch die nebenstehende Skizze definiert. Für (x, y) können nur Werte innerhalb des durch die drei Eckpunkte (0, 1), (4, 3) und (4, 5) festgelegten dreieckförmigen Gebietes auftreten. Innerhalb des Dreiecks sind alle Zufallsgrößen (x, y) gleichwahrscheinlich. Für die 2D–WDF gilt somit:
- $$f_{xy}(x,y) = A .$$
- Zusätzlich ist die Gerade x = y ⇒ „Winkelhalbierende” in obiger Skizze eingezeichnet (siehe Teilaufgabe 2).
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 4.1.
Fragebogen
Musterlösung
- 1. Das Volumen unter der zweidimensionalen WDF ist definitionsgemäß gleich 1:
- $$\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x\, {\rm d}y=1.$$
- Die Dreiecksfläche ist D = 0.5 · 2 · 4 = 4. Da in diesem Definitionsgebiet die WDF konstant gleich A ist, erhält man A = 1/D = 0.25.
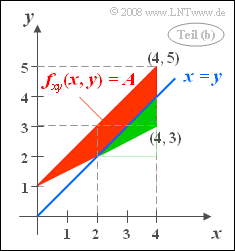
- 2. Zur Lösung gehen wir von nebenstehender Skizze aus. Das Gebiet „x > y“ liegt rechts von der Winkelhalbierenden x = y und ist grün markiert.
- Die Dreiecksfläche ist Db = 0.5 · 1 · 2 = 1, also genau ein Viertel der Gesamtfläche D des Definitionsgebietes. Daraus folgt Pr(x > y) = 0.25.
- 3. Für die gesuchte Rand-WDF gilt in diesem Fall:
- $$f_x(x)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}y=A\cdot B_y (x).$$
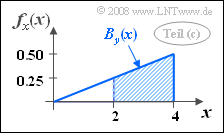
- Hierbei bezeichnet By(x) die Breite des Gebietes „fxy ≠ 0“ in y-Richtung beim betrachteten x-Wert. Es gilt: By(x) = x/2. Mit A = 0.25 folgt für 0 ≤ x ≤ 4: fx(x) = x/8.
- Die gesuchte Wahrscheinlichkeit entspricht der schraffierten Fläche in nebenstehender Skizze. Man erhält:
- $$\rm Pr(\it x\ge \rm 2) = \rm 1-\rm Pr(\it x < \rm 2) \\ = \rm 1-\frac{1}{2}\cdot2\cdot 0.25\hspace{0.15cm}\underline{ =0.75}. $$
Zum gleichen Ergebnis gelangt man anhand der 2D-WDF: Rechts von der Senkrechten x = 2 liegt 3/4 des gesamten Definitionsgebiets.
- 4. Analog der Musterlösung zu (c) gilt:
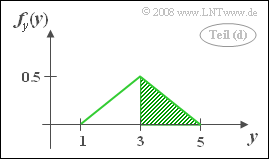
- $$f_y(y)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x=A\cdot B_x (y).$$
- Die Ausbreitung des WDF-Gebietes in x-Richtung ist für y ≤ 1 und y ≥ 5 jeweils 0. Das Maximum liegt bei y = 3: Bx(y = 3) = 2. Dazwischen ist die Zu– und Abnahme von Bx(y) linear und es ergibt sich eine dreieckförmige WDF.
- Die Wahrscheinlichkeit, dass y größer oder gleich 3 ist, entspricht der grün schraffierten Fläche und ergibt aufgrund der Symmetrie den Wert 0.5. Zum gleichen Ergebnis kommt man anhand der 2D–WDF: Oberhalb der Horizontalen y = 3 liegt die Hälfte des gesamten Definitionsgebietes.
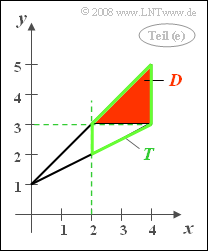
- 5. Wenn y ≥ 3 (rot hinterlegtes Dreieck D) ist, gilt stets auch x ≥ 2 (grün umrandetes Trapez T). Das bedeutet: In diesem Beispiel ist D eine Teilmenge von T, und es gilt:
- $$\rm Pr((\it x \ge \rm 2)\cap(\it y \ge \rm 3)) = \rm Pr(\it y \ge \rm 3) \hspace{0.15cm}\underline{= 0.50}.$$
- 6. Entsprechend der Lösung zur Aufgabe (e) folgt aus „y ≥ 3“ mit Sicherheit auch „x ≥ 2“. Somit ist die gesuchte bedingte Wahrscheinlichkeit gleich 1.
- 7. Die Aufgabe kann man z. B. mit dem Satz von Bayes (siehe Kapitel 1.3) und den Ergebnissen aus (2) und (5) und lösen:
- $$\rm Pr(\it y \ge \rm 3\hspace{0.1cm}|\hspace{0.1cm} \it x \ge \rm 2) = \frac{ \rm Pr((\it x \ge \rm 2)\cap(\it y \ge \rm 3))} {\rm Pr(\it x \ge \rm 2)}\hspace{0.15cm}\underline{=\rm {2}/{3}}.$$
- Oder anders ausgedrückt: Die Fläche D des rot hinterlegten Dreiecks macht 2/3 der Fläche des grün umrandeten Trapezes aus.