Aufgaben:Aufgabe 4.19: Orthogonale mehrstufige FSK: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID2092__Dig_A_4_19.png|right|frame|Signalraumkonstellationen]] | [[Datei:P_ID2092__Dig_A_4_19.png|right|frame|Signalraumkonstellationen]] | ||
| − | Wir betrachten in dieser letzten Übungsaufgabe zu diesem Kapitel | + | Wir betrachten in dieser letzten Übungsaufgabe zu diesem Kapitel "Frequency Shift Keying" $\rm (FSK)$ mit $M$ Signalformen und setzen voraus, dass diese paarweise zueinander orthogonal sind. |
| + | |||
| + | In diesem Fall können die äquivalenten Tiefpass–Signale $s_i(t)$ mit $i = 1, \ \text{...} \ , M$ in folgender Form dargestellt werden: | ||
:$$s_i(t) = \sqrt{E_{\rm S}} \cdot \xi_i(t) \hspace{0.05cm}.$$ | :$$s_i(t) = \sqrt{E_{\rm S}} \cdot \xi_i(t) \hspace{0.05cm}.$$ | ||
| − | $\xi_i(t)$ sind komplexe Basisfunktionen, für die allgemein $i = 1, \ \text{...} \ , N$ gilt. Bei orthogonaler Signalisierung ist allerdings stets $M = N$. | + | *$\xi_i(t)$ sind komplexe Basisfunktionen, für die allgemein $i = 1, \ \text{...} \ , N$ gilt. |
| + | |||
| + | *Bei orthogonaler Signalisierung ist allerdings stets $M = N$. | ||
| + | |||
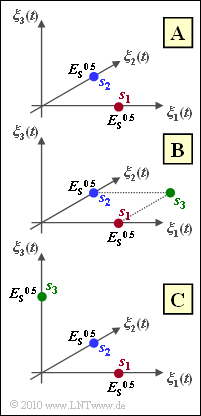
| + | *Die Grafik zeigt drei verschiedene Signalraumkonstellationen. Jedoch beschreiben nicht alle drei eine orthogonale FSK. Hierauf wird in der Teilaufgabe '''(1)''' Bezug genommen. | ||
| − | |||
Im [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation| Theorieteil]] ist die exakte Formel für die Wahrscheinlichkeit einer korrekten Entscheidung bei AWGN–Störung angegeben: | Im [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation| Theorieteil]] ist die exakte Formel für die Wahrscheinlichkeit einer korrekten Entscheidung bei AWGN–Störung angegeben: | ||
| Zeile 14: | Zeile 19: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Daraus lässt sich sehr einfach die Symbolfehlerwahrscheinlichkeit berechnen: | + | *Daraus lässt sich sehr einfach die Symbolfehlerwahrscheinlichkeit berechnen: |
:$$p_{\rm S} = {\rm Pr}({\cal{E}}) = 1 - {\rm Pr}({\cal{C}}) = \sum_{i = 1}^{M-1} (-1)^{i+1} \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm e }^{ - i/(i+1) \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm S}/ N_0} | :$$p_{\rm S} = {\rm Pr}({\cal{E}}) = 1 - {\rm Pr}({\cal{C}}) = \sum_{i = 1}^{M-1} (-1)^{i+1} \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm e }^{ - i/(i+1) \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm S}/ N_0} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Eine obere Schranke $(p_{\rm S, \ max} ≥ p_{\rm S})$ ergibt sich aufgrund der alternierenden Vorzeichen, wenn man von dieser Summe nur den ersten Term $(i=1)$ berücksichtigt: | + | *Eine obere Schranke $(p_{\rm S, \ max} ≥ p_{\rm S})$ ergibt sich aufgrund der alternierenden Vorzeichen, wenn man von dieser Summe nur den ersten Term $(i=1)$ berücksichtigt: |
:$$p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})} | :$$p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In der Teilaufgabe '''(4)''' soll diese Schranke bei gegebenem Verhältnis $E_{\rm B}/N_0$ ausgewertet werden, wobei $E_{\rm B}$ die mittlere Signalenergie pro Bit angibt: | + | *In der Teilaufgabe '''(4)''' soll diese Schranke bei gegebenem Verhältnis $E_{\rm B}/N_0$ ausgewertet werden, wobei $E_{\rm B}$ die mittlere Signalenergie pro Bit angibt: |
:$$E_{\rm B} = \frac{ E_{\rm S} } { {\rm log_2}\hspace{0.1cm}(M)} | :$$E_{\rm B} = \frac{ E_{\rm S} } { {\rm log_2}\hspace{0.1cm}(M)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 28: | Zeile 33: | ||
| + | Hinweise: | ||
| + | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation| "Trägerfrequenzsysteme mit nichtkohärenter Demodulation"]]. | ||
| − | + | * Bezug genommen wird insbesondere auf die Seite [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation#Nichtkoh.C3.A4rente_Demodulation_von_mehrstufiger_FSK|"Nichtkohärente Demodulation von mehrstufiger FSK"]]. | |
| − | |||
| − | |||
| − | |||
| − | * Bezug genommen wird insbesondere auf die Seite [[Digitalsignal%C3%BCbertragung/Tr%C3%A4gerfrequenzsysteme_mit_nichtkoh%C3%A4renter_Demodulation#Nichtkoh.C3.A4rente_Demodulation_von_mehrstufiger_FSK|Nichtkohärente Demodulation von mehrstufiger FSK]]. | ||
| Zeile 40: | Zeile 43: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche der obigen Signalraumkonstellationen gelten für orthogonale FSK? | + | {Welche der obigen Signalraumkonstellationen gelten für eine orthogonale FSK? |
|type="[]"} | |type="[]"} | ||
+ Konstellation $\rm A$, | + Konstellation $\rm A$, | ||
| Zeile 46: | Zeile 49: | ||
+ Konstellation $\rm C$. | + Konstellation $\rm C$. | ||
| − | {Berechnen Sie für $E_{\rm S}/N_0 = 6$ die Fehlerwahrscheinlichkeit der binären, ternären und quaternären FSK. $E_{\rm S}$ bezeichnet die Symbolenergie. | + | {Berechnen Sie für $E_{\rm S}/N_0 = 6$ die Fehlerwahrscheinlichkeit der binären, ternären und quaternären FSK. $E_{\rm S}$ bezeichnet die Symbolenergie. |
|type="{}"} | |type="{}"} | ||
$M = 2 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ { 2.49 3% } $\ \%$ | $M = 2 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ { 2.49 3% } $\ \%$ | ||
| Zeile 58: | Zeile 61: | ||
$M = 4 \text{:} \hspace{0.4cm} p_{\rm S, \ max} \ = \ $ { 7.47 3% } $\ \%$ | $M = 4 \text{:} \hspace{0.4cm} p_{\rm S, \ max} \ = \ $ { 7.47 3% } $\ \%$ | ||
| − | {Berechnen Sie für $E_{\rm B}/N_0 = 6$ die Fehlerwahrscheinlichkeit der binären, ternären und quaternären FSK. $E_{\rm B}$ bezeichnet die Bitenergie. | + | {Berechnen Sie für $E_{\rm B}/N_0 = 6$ die Fehlerwahrscheinlichkeit der binären, ternären und quaternären FSK. $E_{\rm B}$ bezeichnet die Bitenergie. |
|type="{}"} | |type="{}"} | ||
$M = 2 \text{:} \hspace{0.4cm} p_{\rm S, \ max} \ = \ $ { 2.49 3% } $\ \%$ | $M = 2 \text{:} \hspace{0.4cm} p_{\rm S, \ max} \ = \ $ { 2.49 3% } $\ \%$ | ||
| Zeile 67: | Zeile 70: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u> | + | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: |
| + | *Bei der Konstellation $\rm B$ ist die Orthogonalität nicht gegeben. | ||
| + | *Vielmehr gilt hier $M = 3$ und $N = 2$. | ||
| − | '''(2)''' Für die binäre FSK $(M = 2)$ gilt mit der Abkürzung $x = E_{\rm S}/N_0 = 6$: | + | |
| − | :$$p_{\rm S} = (-1)^{2} \cdot {1 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-x/2 } = {1}/{2} \cdot {\rm e }^{-3} \underline{\approx 2.49 \%} | + | |
| + | '''(2)''' Für die binäre FSK $(M = 2)$ gilt mit der Abkürzung $x = E_{\rm S}/N_0 = 6$: | ||
| + | :$$p_{\rm S} = (-1)^{2} \cdot {1 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-x/2 } = {1}/{2} \cdot {\rm e }^{-3} \hspace{0.15cm}\underline{\approx 2.49 \%} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Entsprechend erhält man für die ternäre FSK $(M = 3)$: | + | *Entsprechend erhält man für die ternäre FSK $(M = 3)$: |
:$$p_{\rm S} = (-1)^{2} \cdot {2 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-(1/2) \hspace{0.05cm} \cdot \hspace{0.05cm} x} + | :$$p_{\rm S} = (-1)^{2} \cdot {2 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-(1/2) \hspace{0.05cm} \cdot \hspace{0.05cm} x} + | ||
(-1)^{3} \cdot {2 \choose 2 } \cdot {1}/{3}\cdot {\rm e }^{-(2/3) \hspace{0.05cm} \cdot \hspace{0.05cm} x}= | (-1)^{3} \cdot {2 \choose 2 } \cdot {1}/{3}\cdot {\rm e }^{-(2/3) \hspace{0.05cm} \cdot \hspace{0.05cm} x}= | ||
| − | {\rm e }^{-3} - {1}/{3} \cdot {\rm e }^{-4} \approx 0.0498 - 0.0061 \underline{ =4.37\%} | + | {\rm e }^{-3} - {1}/{3} \cdot {\rm e }^{-4} \approx 0.0498 - 0.0061 \hspace{0.15cm}\underline{ =4.37\%} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Schließlich ergibt sich für die quaternäre FSK $(M = 4)$: | + | *Schließlich ergibt sich für die quaternäre FSK $(M = 4)$: |
:$$p_{\rm S} = (-1)^{2} \cdot {3 \choose 1 } \cdot \frac{{\rm e }^{-x/2}}{2} + | :$$p_{\rm S} = (-1)^{2} \cdot {3 \choose 1 } \cdot \frac{{\rm e }^{-x/2}}{2} + | ||
(-1)^{3} \cdot {3 \choose 2 } \cdot \frac{{\rm e }^{-2x/3}}{3} | (-1)^{3} \cdot {3 \choose 2 } \cdot \frac{{\rm e }^{-2x/3}}{3} | ||
+ (-1)^{4} \cdot {4 \choose 3 } \cdot \frac{{\rm e }^{-3x/4 }}{4} = | + (-1)^{4} \cdot {4 \choose 3 } \cdot \frac{{\rm e }^{-3x/4 }}{4} = | ||
| − | {3}/ {2} \cdot{\rm e }^{-3} - {\rm e }^{-4} + {\rm e }^{-4.5} \underline{\approx 6.75\%} | + | {3}/ {2} \cdot{\rm e }^{-3} - {\rm e }^{-4} + {\rm e }^{-4.5} \hspace{0.15cm}\underline{\approx 6.75\%} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(3)''' Bei gleichem $E_{\rm S}/N_0 = 6$ gilt stets $p_{\rm S, \ max} ≥ p_{\rm S}$: | |
| − | + | :$$M =2\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=2.49\%} = p_{\rm S} \hspace{0.05cm},$$ | |
| − | + | :$$M =3\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=4.98\%} > 4.37\% = p_{\rm S} \hspace{0.05cm},$$ | |
| − | + | :$$M =4\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=7.47\%} > {6.75\%} = p_{\rm S} \hspace{0.05cm}.$$ | |
| + | Analysiert man die Gleichung $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ genauer, so erkennt man, dass diese Schranke genau die [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit#Union_Bound_-_Obere_Schranke_f.C3.BCr_die_Fehlerwahrscheinlichkeit| "Union–Bound"]] angibt: | ||
| + | * Beim Binärsystem gibt $1/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ die Verfälschungswahrscheinlichkeit an, zum Beispiel von $\boldsymbol{s}_1$ nach $\boldsymbol{s}_2$ oder umgekehrt. | ||
| − | + | * Beim $M$–stufigen System ist der Abstand zwischen $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ genau so groß. Aber auch die Punkte $\boldsymbol{s}_3, \ \text{... ,} \, \boldsymbol{s}_M$ liegen im gleichen Abstand zu $\boldsymbol{s}_1$ bzw. zu $\boldsymbol{s}_2$. | |
| − | * | + | * Die „Union–Bound” berücksichtigt die Verfälschungsmöglichkeiten eines Punktes zu jedem der allgemein $M–1$ anderen Punkte durch den Faktor $M -1$. |
| − | *Der Faktor $M& | + | |
| + | |||
| + | '''(4)''' Mit $E_{\rm B} = E_{\rm S}/{\rm log}_2(M)$ erhält man $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-\log_2 \ (M) E_{\rm B}/(2N_{\rm 0})}$. | ||
| + | |||
| + | *Die Fehlerwahrscheinlichkeit wird mit zunehmender Stufenzahl kleiner, da bei konstantem $E_{\rm B}$ die Energie $E_{\rm S}$ pro Symbol um den Faktor ${\rm log}_2 \, (M)$ zunimmt. | ||
| + | |||
| + | *Der Faktor $M-1$ $($berücksichtigt die Verfälschungsmöglichkeiten eines Signalraumpunktes$)$ hat weniger Einfluss als die Vergrößerung des negativen Exponenten: | ||
:$$M =2\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{ 2} \cdot {\rm e }^{-3} \hspace{0.15cm} \underline{= 2.49\%} \hspace{0.05cm},$$ | :$$M =2\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{ 2} \cdot {\rm e }^{-3} \hspace{0.15cm} \underline{= 2.49\%} \hspace{0.05cm},$$ | ||
:$$M =3\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{-4.755} \hspace{0.5cm} \underline{= 0.86\%} \hspace{0.05cm},$$ | :$$M =3\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{-4.755} \hspace{0.5cm} \underline{= 0.86\%} \hspace{0.05cm},$$ | ||
Aktuelle Version vom 31. August 2022, 14:40 Uhr
Wir betrachten in dieser letzten Übungsaufgabe zu diesem Kapitel "Frequency Shift Keying" $\rm (FSK)$ mit $M$ Signalformen und setzen voraus, dass diese paarweise zueinander orthogonal sind.
In diesem Fall können die äquivalenten Tiefpass–Signale $s_i(t)$ mit $i = 1, \ \text{...} \ , M$ in folgender Form dargestellt werden:
- $$s_i(t) = \sqrt{E_{\rm S}} \cdot \xi_i(t) \hspace{0.05cm}.$$
- $\xi_i(t)$ sind komplexe Basisfunktionen, für die allgemein $i = 1, \ \text{...} \ , N$ gilt.
- Bei orthogonaler Signalisierung ist allerdings stets $M = N$.
- Die Grafik zeigt drei verschiedene Signalraumkonstellationen. Jedoch beschreiben nicht alle drei eine orthogonale FSK. Hierauf wird in der Teilaufgabe (1) Bezug genommen.
Im Theorieteil ist die exakte Formel für die Wahrscheinlichkeit einer korrekten Entscheidung bei AWGN–Störung angegeben:
- $${\rm Pr}({\cal{C}}) =\sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm e }^{ - i/(i+1) \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm S}/ N_0} \hspace{0.05cm}.$$
- Daraus lässt sich sehr einfach die Symbolfehlerwahrscheinlichkeit berechnen:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) = 1 - {\rm Pr}({\cal{C}}) = \sum_{i = 1}^{M-1} (-1)^{i+1} \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm e }^{ - i/(i+1) \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm S}/ N_0} \hspace{0.05cm}.$$
- Eine obere Schranke $(p_{\rm S, \ max} ≥ p_{\rm S})$ ergibt sich aufgrund der alternierenden Vorzeichen, wenn man von dieser Summe nur den ersten Term $(i=1)$ berücksichtigt:
- $$p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})} \hspace{0.05cm}.$$
- In der Teilaufgabe (4) soll diese Schranke bei gegebenem Verhältnis $E_{\rm B}/N_0$ ausgewertet werden, wobei $E_{\rm B}$ die mittlere Signalenergie pro Bit angibt:
- $$E_{\rm B} = \frac{ E_{\rm S} } { {\rm log_2}\hspace{0.1cm}(M)} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Trägerfrequenzsysteme mit nichtkohärenter Demodulation".
- Bezug genommen wird insbesondere auf die Seite "Nichtkohärente Demodulation von mehrstufiger FSK".
Fragebogen
Musterlösung
- Bei der Konstellation $\rm B$ ist die Orthogonalität nicht gegeben.
- Vielmehr gilt hier $M = 3$ und $N = 2$.
(2) Für die binäre FSK $(M = 2)$ gilt mit der Abkürzung $x = E_{\rm S}/N_0 = 6$:
- $$p_{\rm S} = (-1)^{2} \cdot {1 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-x/2 } = {1}/{2} \cdot {\rm e }^{-3} \hspace{0.15cm}\underline{\approx 2.49 \%} \hspace{0.05cm}.$$
- Entsprechend erhält man für die ternäre FSK $(M = 3)$:
- $$p_{\rm S} = (-1)^{2} \cdot {2 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-(1/2) \hspace{0.05cm} \cdot \hspace{0.05cm} x} + (-1)^{3} \cdot {2 \choose 2 } \cdot {1}/{3}\cdot {\rm e }^{-(2/3) \hspace{0.05cm} \cdot \hspace{0.05cm} x}= {\rm e }^{-3} - {1}/{3} \cdot {\rm e }^{-4} \approx 0.0498 - 0.0061 \hspace{0.15cm}\underline{ =4.37\%} \hspace{0.05cm}.$$
- Schließlich ergibt sich für die quaternäre FSK $(M = 4)$:
- $$p_{\rm S} = (-1)^{2} \cdot {3 \choose 1 } \cdot \frac{{\rm e }^{-x/2}}{2} + (-1)^{3} \cdot {3 \choose 2 } \cdot \frac{{\rm e }^{-2x/3}}{3} + (-1)^{4} \cdot {4 \choose 3 } \cdot \frac{{\rm e }^{-3x/4 }}{4} = {3}/ {2} \cdot{\rm e }^{-3} - {\rm e }^{-4} + {\rm e }^{-4.5} \hspace{0.15cm}\underline{\approx 6.75\%} \hspace{0.05cm}.$$
(3) Bei gleichem $E_{\rm S}/N_0 = 6$ gilt stets $p_{\rm S, \ max} ≥ p_{\rm S}$:
- $$M =2\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=2.49\%} = p_{\rm S} \hspace{0.05cm},$$
- $$M =3\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=4.98\%} > 4.37\% = p_{\rm S} \hspace{0.05cm},$$
- $$M =4\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=7.47\%} > {6.75\%} = p_{\rm S} \hspace{0.05cm}.$$
Analysiert man die Gleichung $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ genauer, so erkennt man, dass diese Schranke genau die "Union–Bound" angibt:
- Beim Binärsystem gibt $1/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ die Verfälschungswahrscheinlichkeit an, zum Beispiel von $\boldsymbol{s}_1$ nach $\boldsymbol{s}_2$ oder umgekehrt.
- Beim $M$–stufigen System ist der Abstand zwischen $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ genau so groß. Aber auch die Punkte $\boldsymbol{s}_3, \ \text{... ,} \, \boldsymbol{s}_M$ liegen im gleichen Abstand zu $\boldsymbol{s}_1$ bzw. zu $\boldsymbol{s}_2$.
- Die „Union–Bound” berücksichtigt die Verfälschungsmöglichkeiten eines Punktes zu jedem der allgemein $M–1$ anderen Punkte durch den Faktor $M -1$.
(4) Mit $E_{\rm B} = E_{\rm S}/{\rm log}_2(M)$ erhält man $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-\log_2 \ (M) E_{\rm B}/(2N_{\rm 0})}$.
- Die Fehlerwahrscheinlichkeit wird mit zunehmender Stufenzahl kleiner, da bei konstantem $E_{\rm B}$ die Energie $E_{\rm S}$ pro Symbol um den Faktor ${\rm log}_2 \, (M)$ zunimmt.
- Der Faktor $M-1$ $($berücksichtigt die Verfälschungsmöglichkeiten eines Signalraumpunktes$)$ hat weniger Einfluss als die Vergrößerung des negativen Exponenten:
- $$M =2\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{ 2} \cdot {\rm e }^{-3} \hspace{0.15cm} \underline{= 2.49\%} \hspace{0.05cm},$$
- $$M =3\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{-4.755} \hspace{0.5cm} \underline{= 0.86\%} \hspace{0.05cm},$$
- $$M =4\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {3}/{ 2} \cdot {\rm e }^{-6} \hspace{0.15cm} \underline{=0.37\%} \hspace{0.05cm}.$$