Aufgabe 4.16: Binary Frequency Shift Keying
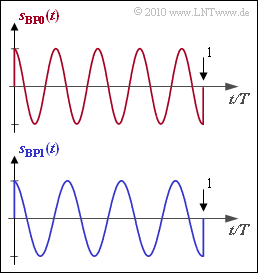
Bei der binären FSK werden die beiden Nachrichten $m_0$ und $m_1$ durch zwei unterschiedliche Frequenzen dargestellt. Für die beiden möglichen Bandpass–Signale gilt dann jeweils im Bereich $0 ≤ t ≤ T$ mit $f_0 = f_{\rm T} + \Delta f_{\rm A}$ sowie $f_1 = f_{\rm T} \, – \Delta f_{\rm A}$:
- $$s_{\rm BP0}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{2E/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},$$
- $$ s_{\rm BP1}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{2E/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm}.$$
Die Grafik zeigt beispielhafte Signale. In obiger Gleichung gibt $f_{\rm T}$ die Trägerfrequenz an und $\Delta f_{\rm A}$ den Frequenzhub als die maximale Abweichung der Augenblicksfrequenz von der Trägerfrequenz an. $T$ ist die Symboldauer und $E$ die Signalenergie. Dabei gilt gleichermaßen für die mittlere Symbolenergie und die mittlere Bitenergie:
- $$E_{\rm S} = E_{\rm B} = E\hspace{0.05cm}.$$
Meist arbeitet man mit dem Modulationsindex, der als das Verhältnis von Gesamtfrequenzhub und Symbolrate definiert ist:
- $$h = \frac{2 \cdot \Delta f_{\rm A}}{1/T} = 2 \cdot \Delta f_{\rm A} \cdot T \hspace{0.05cm}.$$
Die äquivalente Tiefpassdarstellung führt unter Verwendung von $h$ zu den beiden komplexen Signalen
- $$ s_{\rm TP0}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$
- $$ s_{\rm TP1}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm}.$$
Eine orthogonale FSK liegt vor, wenn das innere Produkt den Wert $0$ ergibt:
- $$< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t =0 \hspace{0.05cm}.$$
In diesem Fall ist auch eine nichtkohärente Demodulation wie im Kapitel Trägerfrequenzensysteme mit nichtkohärenter Demodulation beschrieben möglich.
Das innere Produkt der BP–Signale kann aus dem inneren Produkt der TP–Signale ermittelt werden:
- $$< \hspace{-0.05cm}s_{\rm BP0}(t) \cdot s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \hspace{0.1cm}< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.15cm} \right ]\hspace{0.05cm}.$$
Gilt $〈 s_{\rm BP0}(t) \cdot s_{\rm BP1}(t)〉 = 0$, aber gleichzeitig auch $〈 s_{\rm TP0}(t) \cdot s_{\rm TP1}(t)〉 ≠ 0$, so ist zwar eine kohärente Demodulation möglich, aber keine nichtkohärente.
Hinweise:
Fragebogen
Musterlösung