Aufgaben:Aufgabe 4.13: Gaußförmige AKF: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Leistungsdichtespektrum (LDS) }} right| :Der hier betrachtete Zufallspr…“) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID411__Sto_A_4_13.png|right|]] | + | [[Datei:P_ID411__Sto_A_4_13.png|right|Zweimal gaußförmige AKF]] |
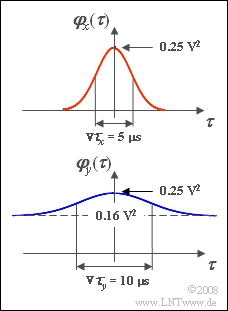
| − | + | Der hier betrachtete Zufallsprozess $\{x_i(t)\}$ sei durch die oben skizzierte Autokorrelationsfunktion (AKF) charakterisiert. | |
| + | Dieser Zufallsprozess ist mittelwertfrei und die äquivalente AKF-Dauer beträgt ${ {\rm \nabla} }\tau_x = 5 \hspace{0.05cm} \rm \mu s$: | ||
:$$\varphi_x(\it \tau)=\rm 0.25 V^2\cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}{/ 5 {\rm\mu}s })^2} .$$ | :$$\varphi_x(\it \tau)=\rm 0.25 V^2\cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}{/ 5 {\rm\mu}s })^2} .$$ | ||
| − | |||
| − | + | Im unteren Bild ist die AKF des Prozesses $\{y_i(t)\}$ dargestellt. Diese lautet mit der äquivalenten AKF-Dauer ${ {\rm \nabla} }\tau_y = 10 \hspace{0.05cm} \rm \mu s$: | |
:$$ \varphi_y(\it \tau)=\rm 0.16 V^2 + \rm 0.09 V^2\cdot\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}/{\nabla \it \tau_y})^2} .$$ | :$$ \varphi_y(\it \tau)=\rm 0.16 V^2 + \rm 0.09 V^2\cdot\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}/{\nabla \it \tau_y})^2} .$$ | ||
| − | + | In dieser Aufgabe werden die Leistungsdichtespektren der beiden Prozesse gesucht. | |
| − | : | + | |
| − | :$$\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\it f}/{\rm \Delta\it f})^2}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, {\rm \Delta \it f} \cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\rm \Delta\it f} \cdot \it t )^{\rm 2}}.$$ | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum]]. | ||
| + | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Zur Lösung dieser Aufgabe können Sie die folgende Fourierkorrespondenz benutzen: | ||
| + | :$$\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\it f}/{\rm \Delta\it f})^2}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, {\rm \Delta \it f} \cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\rm \Delta\it f} \hspace{0.03cm}\cdot \hspace{0.03cm}\it t )^{\rm 2}}.$$ | ||
Version vom 27. März 2017, 15:37 Uhr
Der hier betrachtete Zufallsprozess $\{x_i(t)\}$ sei durch die oben skizzierte Autokorrelationsfunktion (AKF) charakterisiert. Dieser Zufallsprozess ist mittelwertfrei und die äquivalente AKF-Dauer beträgt ${ {\rm \nabla} }\tau_x = 5 \hspace{0.05cm} \rm \mu s$:
- $$\varphi_x(\it \tau)=\rm 0.25 V^2\cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}{/ 5 {\rm\mu}s })^2} .$$
Im unteren Bild ist die AKF des Prozesses $\{y_i(t)\}$ dargestellt. Diese lautet mit der äquivalenten AKF-Dauer ${ {\rm \nabla} }\tau_y = 10 \hspace{0.05cm} \rm \mu s$:
- $$ \varphi_y(\it \tau)=\rm 0.16 V^2 + \rm 0.09 V^2\cdot\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}/{\nabla \it \tau_y})^2} .$$
In dieser Aufgabe werden die Leistungsdichtespektren der beiden Prozesse gesucht.
Hinweise:
- Die Aufgabe gehört zum Kapitel Leistungsdichtespektrum.
- Bezug genommen wird auch auf das Kapitel Autokorrelationsfunktion.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Zur Lösung dieser Aufgabe können Sie die folgende Fourierkorrespondenz benutzen:
- $$\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\it f}/{\rm \Delta\it f})^2}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, {\rm \Delta \it f} \cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\rm \Delta\it f} \hspace{0.03cm}\cdot \hspace{0.03cm}\it t )^{\rm 2}}.$$
Fragebogen
Musterlösung
- 1. Die äquivalente LDS-Bandbreite ist der Kehrwert der äquivalenten AKF-Dauer:
- $$\nabla f_x = 1 / \nabla \tau_x \hspace{0.15cm}\underline{= {\rm 200\hspace{0.1cm}kHz}}.$$
- 2. Die angegebene Fourierkorrespondenz kann man wie folgt an die Aufgabenstellung anpassen:
- $$K\cdot{\rm e}^{-\pi({\tau}/{\nabla\tau_x})^2}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\frac{\it K}{\nabla \it f_x}\cdot{\rm e}^{-\pi({f}/{\nabla f_x})^2}.$$
- Mit K = 0.25 V2 und ∇fx = 200 kHz erhält man:
- $${\it \Phi_x}(f)=1.25\cdot\rm 10^{-\rm 6}\hspace{0.1cm}\frac{V^2}{Hz}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_x})^2}.$$
- Bei der Frequenz f = 0 ergibt sich somit 1.25 · 10–6 V2/Hz. Der LDS-Wert bei f = 200 kHz = ∇fx ist um den Faktor e–π kleiner, beträgt also 5.4 · 10 –8 V2/Hz.
- 3. Ein mittelwertfreier Prozess hat stets ein kontinuierliches LDS zur Folge. Dieses ist um so schmaler, je breiter die AKF ist (Reziprozitätsgesetz). Da die Prozessleistung gleich dem Integral über das LDS ist, muss bei konstanter Prozessleistung eine breitere AKF (schmaleres LDS) durch höhere LDS-Werte ausgeglichen werden. Ein Gleichanteil oder periodische Anteile führen stets zu Diracfunktionen im LDS; ansonsten ist das LDS stets wertkontinuierlich. Richtig sind die Lösungsvorschläge 1, 2 und 4.
- 4. Analog zu Teilaufgabe (2) gilt mit ∇fy = 100 kHz:
- $${\it \Phi_y}(f)=\frac{\rm 0.09 V^2}{\nabla\it f_y}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_y})^2}+\it m_y^{\rm 2}\cdot\delta(f).$$
- Aufgrund des Gleichanteils gibt es zusätzlich zum kontinuierlichen LDS-Anteil noch einen Dirac bei der Frequenz f = 0. Der kontinuierliche LDS–Anteil bei f = 0 beträgt 0.9 · 10–6 V2/Hz. Der Anteil bei f = 2 · ∇fy = 200 kHz ist deutlich, nämlich um den Faktor e–4 ≈ 7 · 10–18 geringer. Hier lautet das LDS–Ergebnis: 6.44 · 10–24 V2/Hz.
- 5. Das LDS eines mittelwertbehafteten Prozesses beinhaltet allgemein eine Diracfunktion bei f = 0 mit Gewicht my2; im vorliegenden Fall ist dieser Wert gleich 0.16 V2. Da δ(f) die Einheit 1/Hz = s besitzt, unterscheiden sich die Einheiten des kontinuierlichen und des diskreten LDS-Anteils. Richtig ist also nur der zweite Lösungsvorschlag.