Aufgabe 4.13: Decodierung von LDPC–Codes

Gegebene LDPC–Prüfmatrix

Die Aufgabe behandelt die Iterative Decodierung von LDPC–Codes gemäß dem Message–passing Algorithmus.

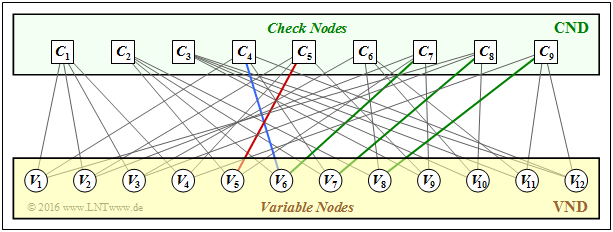
Ausgangspunkt ist die dargestellte $9 × 12$–Prüfmatrix $\mathbf{H}$, die zu Beginn der Aufgabe als Tanner–Graph dargestellt werden soll. Dabei ist anzumerken:

Die Variable Nodes (abgekürzt $\rm VNs$) $V_i$ bezeichnen die $n$ Codewortbits.
Die Check Nodes (abgekürzt $\rm CNs$) $C_j$ stehen für die $m$ Prüfgleichungen.
Eine Verbindung zwischen $V_i$ und $C_j$ zeigt an, dass das Matrixelement $h_{j,\hspace{0.05cm} i}$ der Prüfmatrix $\mathbf{H}$ (in Zeile $j$, Spalte $i$) gleich $1$ ist. Für $h_{j,\hspace{0.05cm}i} = 0$ gibt es keine Verbindung zwischen $V_i$ und $C_j$.
Als die Nachbarn $N(V_i)$ von $V_i$ bezeichnet man die Menge aller Check Nodes $C_j$, die mit $V_i$ im Tanner–Graphen verbunden sind. Entsprechend gehören zu $N(C_j)$ alle Variable Nodes $V_i$ mit einer Verbindung zu $C_j$.

Die Decodierung erfolgt abwechselnd bezüglich

den Variable Nodes ⇒ Variable Nodes Decoder (VND), und
den Check Nodes ⇒ Check Nodes Decoder (CND).

Hierauf wird in den Teilaufgaben (5) und (6) Bezug genommen.

Hinweise:

Die Aufgabe gehört zum Themengebiet des Kapitels Grundlegendes zu den Low–density Parity–check Codes.
Bezug genommen wird insbesondere auf die Seite Iterative Decodierung von LDPC–Codes.

Fragebogen

Musterlösung

(1) Der Variable Node $\rm (VN)$ $V_i$ steht für das $i$–te Codewortbit, so dass $I_{\rm VN}$ gleich der Codewortlänge $n$ ist.

Aus der Spaltenzahl der $\mathbf{H}$–Matrix erkennt man $I_{\rm VN} = n \ \underline{= 12}$.
Für die Menge aller Variable Nodes kann man somit allgemein schreiben: ${\rm VN} = \{V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , V_i, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ V_n\}$.
Der Check Node ${\rm (CN)} \ C_j$ steht für die $j$–Prüfgleichung, und für die Menge aller Check Nodes gilt: ${\rm CN} = \{C_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_j, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_m\}$.
Aus der Zeilenzahl der $\mathbf{H}$–Matrix ergibt sich $I_{\rm CN} \ \underline {= m = 9}$.

(2) Die Ergebnisse können aus dem nachfolgend skizzierten Tanner–Graphen abgelesen werden.

Tanner–Graph für das vorliegende Beispiel

Richtig sind die Lösungsvorschläge 1, 2 und 5:

Das Matrixelement $h_{5,\hspace{0.05cm}5}$ (Spalte 5, Zeile 5) ist $1$ ⇒ rote Verbindung.
Das Matrixelement $h_{4,\hspace{0.05cm} 6}$ (Spalte 4, Zeile 6) ist $1$ ⇒ blaue Verbindung.
Das Matrixelement $h_{6, \hspace{0.05cm}4}$ (Spalte 6, Zeile 4) ist $0$ ⇒ keine Verbindung.
Es gilt $h_{6,\hspace{0.05cm} 10} = h_{6,\hspace{0.05cm} 11} = 1$. Aber $h_{6,\hspace{0.05cm}11} = 0$ ⇒ es bestehen nicht alle drei Verbindungen.
Es gilt $h_{7,\hspace{0.05cm}6} = h_{8,\hspace{0.05cm}7} = h_{9,\hspace{0.05cm}8} = 1$ ⇒ grüne Verbindungen.

(3) Es handelt sich um einen regulären LDPC–Code mit

$w_{\rm Z}(j) = 4 = w_{\rm Z}$ für $1 ≤ j ≤ 9$,
$w_{\rm S}(i) = 3 = w_{\rm S}$ für $1 ≤ i ≤ 12$.

Die Antworten 2 und 3 sind richtig, wie aus der ersten Zeile bzw. der neunten Spalte der Prüfmatrix $\mathbf{H}$ hervorgeht. Der Tanner–Graph bestätigt diese Ergebnisse:

Von $C_1$ gibt es Verbindungen zu $V_1, \ V_2, \ V_3$, und $V_4$.
Von $V_9$ gibt es Verbindungen zu $C_3, \ C_5$, und $C_7$.

Die Antworten 1 und 4 können schon allein deshalb nicht richtig sein, da

die Nachbarschaft $N(V_i)$ eines jeden Variable Nodes $V_i$ genau $w_{\rm S} = 3$ Elemente beinhaltet, und
die Nachbarschaft $N(C_j)$ eines jeden Check Nodes $C_j$ genau $w_{\rm Z} = 4$ Elemente.

(4) Richtig sind die Lösungsvorschläge 1 und 2, wie aus der entsprechenden Theorieseite hervorgeht:

Zu Beginn der Decodierung (sozusagen bei der Iteration $I=0$) werden die $L$–Werte der Variable Nodes ⇒ $L(V_i)$ entsprechend den Kanaleingangswerten vorbelegt.
Später (ab der Iteration $I = 1$) wird im VND das vom CND übermittelte Log–Likelihood–Verhältnis $L(C_j → V_i)$ als Apriori–Information berücksichtigt.
Die Antwort 3 ist falsch. Richtig wäre vielmehr: Es gibt Analogien zwischen dem VND–Algorithmus und der Decodierung eines Repetition Codes (Wiederholungscodes).

(5) Richtig ist nur der Lösungsvorschlag 3, weil

die endgültigen Aposteriori–$L$–Werte vom VND abgeleitet werden, nicht vom CND,
die $L$–Wert $L(C_j → V_i)$ für den CND extrinsische Information darstellt, und
es tatsächlich Analogien zwischen dem CND–Algorithmus und der SPC–Decodierung gibt.

	$C_4$ und $V_6$.
	$C_5$ und $V_5$.
	$C_6$ und $V_4$.
	$C_6$ und $V_i$ für $i > 9$.
	$C_j$ und $V_{j-1}$ für $j > 6$.

	$N(V_1) = \{C_1, \ C_2, \ C_3, \ C_4\}$,
	$N(C_1) = \{V_1, \ V_2, \ V_3, \ V_4\}$,
	$N(V_9) = \{C_3, \ C_5, \, C_7\}$,
	$N(C_9) = \{V_3, \ V_5, \ V_7\}$.

	Zu Beginn (Iteration 0) werden die $L$–Werte der Knoten $V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, \ V_n$ entsprechend den Kanaleingangswerten $y_i$ vorbelegt.
	Für den VND stellt $L(C_j → V_i)$ Apriori–Information dar.
	Es gibt Analogien zwischen dem VND und der Decodierung eines Single Parity–check Codes-

	Der CND liefert am Ende die gewünschten Aposteriori–$L$–Werte.
	Für den CND stellt $L(C_j → V_i)$ Apriori–Information dar.
	Es gibt Analogien zwischen dem CND und der Decodierung eines Single Parity–check Codes.