Aufgaben:Aufgabe 4.11: On-Off-Keying und Binary Phase Shift Keying

• Zurück zum Buch

Zwei Signalraumkonstellation für OOK und BPSK

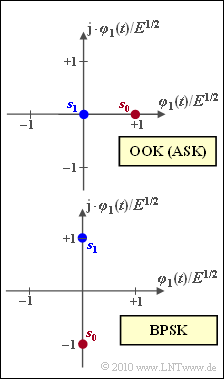
Die Grafik zeigt Signalraumkonstellationen für trägermodulierte Modulationsverfahren:

• On–Off–Keying  (OOK), in manchen Büchern auch als Amplitude Shift Keying  (ASK) bezeichnet,
• Binary Phase Shift Keying  (BPSK).

Für die Berechnung der Fehlerwahrscheinlichkeit gehen wir vom AWGN–Kanal aus. In diesem Fall ist die Fehlerwahrscheinlichkeit (bezogen auf Symbole oder auf Bit gleichermaßen):

$$p_{\rm S} = p_{\rm B} = {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right ) \hspace{0.05cm}.$$

Hierbei bezeichnet

• $d$  den Abstand der Signalraumpunkte, und
• $\sigma_n^2 = N_0/2$  die Varianz des AWGN–Rauschens.

In den Teilfragen ab (3) wird zudem auf die mittlere Symbollenergie  $E_{\rm S}$  Bezug genommen.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Trägerfrequenzsysteme mit kohärenter Demodulation.
• Bezug genommen wird auch auf das Kapitel  Lineare digitale Modulation – Kohärente Demodulation  sowie das Kapitel  Lineare digitale Modulation  des Buches „Modulationsverfahren”.

• Verwenden Sie für die komplementäre Gaußsche Fehlerfunktion die folgende Näherung:

$${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

Fragebogen

1

Wieviele Bit  $(b)$  stellt jeweils ein Symbol dar? Wie groß ist die Stufenzahl  $M$?

$b \hspace{0.35cm} = \ $

$M \ = \ $

2

Welche Darstellung zeigen die Signalraumkonstellationen?

	Die Darstellung im (tatsächlichen) Bandpassbereich,
	die Darstellung im (äquivalenten) Tiefpassbereich.

3

Welche Fehlerwahrscheinlichkeit ergibt sich für On–Off–Keying  abhängig von  $E_{\rm S}/N_0$?

$E_{\rm S}/N_0 = 9 \text{:} \hspace{2.3cm} p_{\rm S} \ = \ $ $\ \cdot 10^{\rm –4}$

$10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 12 \ {\rm dB} \text{:} \hspace{0.2cm} p_{\rm S} \ = \ $ $\ \cdot 10^{\rm –4}$

4

Welche Fehlerwahrscheinlichkeit ergibt sich für Binary Phase Shift Keying abhängig von  $E_{\rm S}/N_0$?

$E_{\rm S}/N_0 = 9 \text{:} \hspace{2.3cm} p_{\rm S} \ = \ $ $\ \cdot 10^{\rm –8}$

$10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 12 \ {\rm dB} \text{:} \hspace{0.2cm} p_{\rm S} \ = \ $ $\ \cdot 10^{\rm –8}$

Musterlösung

Musterlösung

(1)  Sowohl On–Off–Keying (OOK) als auch Binary Phase Shift Keying (BPSK) sind binäre Modulationsverfahren:

$$\underline{b = 1 }\hspace{0.05cm},\hspace{0.5cm} \underline{M = 2} \hspace{0.05cm}.$$

(2)  Richtig ist der Lösungsvorschlag 2, erkennbar an der imaginären Basisfunktion $\varphi_2(t) = {\rm j} \cdot \varphi_1(t)$.

• Bei Beschreibung im Bandpassbereich wären die Basisfunktionen cosinus– und (minus–)sinusförmig reell.

(3)  Die vorgegebene Gleichung lautet bei On–Off–Keying (OOK) mit

• $d = \sqrt {E}$,
• $E_{\rm S} = E/2$ (wobei gleichwahrscheinliche Symbole $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ vorausgesetzt sind) und
• $\sigma_n^2 = N_0/2$:

$$p_{\rm S} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right )= {\rm Q} \left ( \frac{ \sqrt{E}/2}{ \sqrt{N_0/2}}\right ) = {\rm Q} \left ( \sqrt{ \frac{ E/2}{ N_0} }\right ) = {\rm Q} \left ( \sqrt{ { E_{\rm S}}/{ N_0} }\right ) \hspace{0.05cm}.$$

• Für $E_{\rm S}/N_0 = 9 = 3^2$ ergibt sich somit:

$$p_{\rm S} = {\rm Q} (3) \approx \frac{1}{\sqrt{2\pi} \cdot 3} \cdot {\rm e}^{-9/2} = \underline{14.8 \cdot 10^{-4}} \hspace{0.05cm}.$$

• Entsprechend gilt für $10 \cdot {\rm lg} \, (E_{\rm S}/N_0) = 12 \ \rm dB$  ⇒  $E_{\rm S}/N_0 = 15.85$:

$$p_{\rm S} = {\rm Q} (\sqrt{15.85}) \approx \frac{1}{\sqrt{2\pi\cdot 15.85} } \cdot {\rm e}^{-15.85/2} = \underline{0.362 \cdot 10^{-4}} \hspace{0.05cm}.$$

(4)  Im Unterschied zur Teilaufgabe (3) gilt Binary Phase Shift Keying (BPSK)

• $d = 2 \cdot \sqrt {E}$,
• $E_{\rm S} = E$,

beides sogar unabhängig von den Auftrittswahrscheinlichkeiten für $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$.

• Daraus folgt:

$$p_{\rm S} = {\rm Q} \left ( \frac{ \sqrt{E_{\rm S}}}{ \sqrt{N_0/2}}\right ) = {\rm Q} \left ( \sqrt{ { 2E_{\rm S}}/{ N_0} }\right ) \hspace{0.05cm}.$$

• Mit $E_{\rm S}/N_0 = 9$ ergibt sich daraus der Zahlenwert:

$$p_{\rm S} = {\rm Q} (\sqrt{18}) \approx \frac{1}{\sqrt{2\pi\cdot 18} } \cdot {\rm e}^{-18/2} = \underline{117 \cdot 10^{-8}} \hspace{0.05cm}.$$

• Und mit $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 12 \ \rm dB$  ⇒  $2E_{\rm S}/N_0 = 31.7$:

$$p_{\rm S} = {\rm Q} (\sqrt{31.7}) \approx \frac{1}{\sqrt{2\pi\cdot 31.7} } \cdot {\rm e}^{-31.7/2} = \underline{0.926 \cdot 10^{-8}}\hspace{0.05cm}.$$