Aufgaben:Aufgabe 4.09: Zykloergodizität: Unterschied zwischen den Versionen
| Zeile 15: | Zeile 15: | ||
*dass die Prozesse zwar im strengen Sinne nicht als stationär und ergodisch zu bezeichnen sind, | *dass die Prozesse zwar im strengen Sinne nicht als stationär und ergodisch zu bezeichnen sind, | ||
*die statistischen Kennwerte aber für Vielfache der Periondauer $T_0$ jeweils gleich sind. | *die statistischen Kennwerte aber für Vielfache der Periondauer $T_0$ jeweils gleich sind. | ||
| + | |||
In diesen Fällen sind auch die meisten der Berechnungsregeln, die eigentlich nur für ergodische Prozesse gelten, anwendbar. | In diesen Fällen sind auch die meisten der Berechnungsregeln, die eigentlich nur für ergodische Prozesse gelten, anwendbar. | ||
| Zeile 37: | Zeile 38: | ||
{Berechnen Sie die Autokorrelationsfunktion $\phi_y(\tau)$ für verschiedene $\tau$-Werte. | {Berechnen Sie die Autokorrelationsfunktion $\phi_y(\tau)$ für verschiedene $\tau$-Werte. | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varphi_y(\tau=0)\ = $ { 2 3% } $\ \rm V^2$ |
| − | $\ | + | $\varphi_y(\tau=0.25 \cdot T_0)\ = $ { 0. } $\ \rm V^2$ |
| − | $\ | + | $\varphi_y(\tau=1.50 \cdot T_0)\ = $ { -2.06--1.94 }$\ \rm V^2$ |
| Zeile 46: | Zeile 47: | ||
+ Alle Mustersignale sind gleichsignalfrei. | + Alle Mustersignale sind gleichsignalfrei. | ||
- Alle Mustersignale besitzen einen Effektivwert von $2\hspace{0.05cm}\rm V$. | - Alle Mustersignale besitzen einen Effektivwert von $2\hspace{0.05cm}\rm V$. | ||
| − | - Die AKF hat die doppelte Periodendauer $(2T_0)$ wie die Mustersignale. | + | - Die AKF hat die doppelte Periodendauer $(2T_0)$ wie die Mustersignale $(T_0)$. |
| Zeile 54: | Zeile 55: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Richtig sind <u>die Lösungsvorschläge 3 und 4</u>: | |
| − | + | *Zum Zeitpunkt $t = 0$ (und allen Vielfachen der Periodendauer $T_0$) hat jedes Mustersignal $x_i(t)$ einen Wert zwischen $1\hspace{0.05cm}\rm V$ und $2\hspace{0.05cm}\rm V$. Der Mittelwert beträgt $1.5\hspace{0.05cm}\rm V$). | |
| − | + | *Dagegen ist bei $t = T_0/4$ der Signalwert des gesamten Ensembles identisch $0$. Das heißt: Bereits der lineare Mittelwert erfüllt die Bedingung der Stationarität nicht; der Prozess $\{x_i(t)\}$ ist nicht stationär und kann deshalb auch nicht ergodisch sein. | |
| − | + | *Dagegen sind beim Prozess $\{y_i(t)\}$ aufgrund der gleichverteilten Phase zu allen Zeitpunkten die gleichen Momente zu erwarten ⇒ der Prozess ist stationär. | |
| − | + | *Da bei der AKF-Berechnung die Phasenbeziehungen verloren gehen, steht jede einzelne Musterfunktion stellvertretend für den gesamten Prozess. Deshalb kann hier hypothetisch von Ergodizität ausgegangen werden. Am Ende der Aufgabe ist zu überprüfen, ob diese Annahme gerechtfertigt ist. | |
| − | |||
| − | |||
| − | |||
| − | + | '''(2)''' Aufgrund der Ergodizität kann jede Musterfunktion zur AKF-Berechung herangezogen werden. Wir benutzen hier willkürlich die Phase $\varphi_i = 0$. Aufgrund der Periodizität genügt die Mitteilung über nur eine Periodendauer $T_0$. Dann gilt: | |
| − | :$$\varphi_y (\tau) = | + | :$$\varphi_y (\tau) = \frac{1}{T_0} \cdot \int_0^{T_0} y(t) \cdot y (t+\tau) \hspace{0.1cm}{\rm d} t = \frac{{ x}_0^2}{{ T}_0} \cdot \int_0^{{\it T}_0} \cos (2 \pi {f_{\rm 0} t}) \cdot \cos (2 \pi {f_{\rm 0} (t+\tau)}) \hspace{0.1cm}\rm d \it t.$$ |
| − | + | Mit der trigonometrischen Beziehung | |
| − | :$$\ | + | :$$\cos (\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \cos (\alpha + \beta) + {1}/{2} \cdot \cos (\alpha - \beta)$$ |
| − | + | folgt daraus weiter: | |
| − | :$$\varphi_y ( | + | :$$\varphi_y (\tau) = \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (4 \pi \it{f_{\rm 0} t} + {\rm 2} \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t + \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (-2 \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t. $$ |
| − | + | Das erste Integral ist $0$ (Integration über zwei Perioden der Cosinusfunktion), der zweite Integrand ist unabhängig von der Integrationsvariablen $t$. Daraus folgt: $\varphi_y (\tau) ={{ x}_0^2}/{\rm 2} \cdot \cos (2 \pi {f_{\rm 0} \tau}). $ Für die angegebenen Zeitpunkte gilt mit $x_0 = 2\hspace{0.05cm}\rm V$: | |
| + | :$$\varphi_y (0)\hspace{0.15cm}\underline{ = 2\hspace{0.05cm}{\rm V}^2}, \hspace{0.5cm} \varphi_y (0.25 \cdot { T}_{\rm 0}{\rm )} \hspace{0.15cm}\underline{ = 0}, \hspace{0.5cm} \varphi_y (\rm 1.5 \cdot {\it T}_{\rm 0} {\rm )} \hspace{0.15cm}\underline{= \rm -2\hspace{0.05cm}{\rm V}^2}.$$ | ||
| − | |||
| − | :Die Periodendauer eines periodischen Zufallsprozesses bleibt in der AKF erhalten, das heißt, auch die Periodendauer der AKF beträgt | + | '''(3)''' Richtig ist nur <u>der erste Lösungsvorschlag</u>: |
| + | *Der Mittelwert $m_y$ kann aus dem Grenzwert der AKF für $\tau \to \infty$ ermittelt werden, wenn man die periodischen Anteile ausschließt. Daraus folgt $m_y= 0$. | ||
| + | *Die Varianz (Leistung) ist gleich dem AKF-Wert an der Stelle $\tau = 0$, also $2\hspace{0.05cm}\rm V^2$. Der Effektivwert ist die Quadratwurzel daraus: $\sigma_y \approx 1.414\hspace{0.05cm}\rm V$. | ||
| + | *Die Periodendauer eines periodischen Zufallsprozesses bleibt in der AKF erhalten, das heißt, auch die Periodendauer der AKF beträgt $T_0$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 24. März 2017, 13:14 Uhr
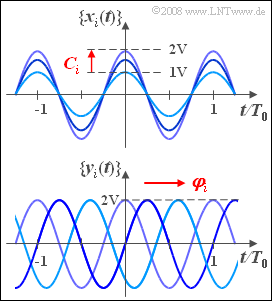
Wir betrachten zwei unterschiedliche Zufallsprozesse, deren Musterfunktionen harmonische Schwingungen mit jeweils gleicher Frequenz $f_0 = 1/T_0$ sind. $T_0$ bezeichnet die Periodendauer.
- Beim oben dargestellten Zufallsprozess $\{x_i(t)\}$ ist die Amplitude die stochastische Komponente, wobei der Zufallsparameter $C_i$ alle Werte zwischen $1\hspace{0.05cm}\rm V$ und $2\hspace{0.05cm}\rm V$ mit gleicher Wahrscheinlichkeit annehmen kann:
- $$\{ x_i(t) \} = \{ C_i \cdot \rm cos (2 \pi \it f_{\rm 0} t)\}. $$
- Beim Prozess $\{y_i(t)\}$ weisen alle Musterfunktionen die gleiche Amplitude auf: $x_0 = 2\hspace{0.05cm}\rm V$. Hier variiert die Phase $\varphi_i$, die gleichverteilt zwischen $0$ und $2\pi$ ist:
- $$\{ y_i(t) \} = \{ x_{\rm 0} \cdot \rm cos (2 \pi \it f_{\rm 0} t - \varphi_i)\}. $$
Die Eigenschaften zyklostationär und zykloergodisch sagen aus,
- dass die Prozesse zwar im strengen Sinne nicht als stationär und ergodisch zu bezeichnen sind,
- die statistischen Kennwerte aber für Vielfache der Periondauer $T_0$ jeweils gleich sind.
In diesen Fällen sind auch die meisten der Berechnungsregeln, die eigentlich nur für ergodische Prozesse gelten, anwendbar.
Hinweise:
- Die Aufgabe gehört zum Kapitel Autokorrelationsfunktion.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- Zum Zeitpunkt $t = 0$ (und allen Vielfachen der Periodendauer $T_0$) hat jedes Mustersignal $x_i(t)$ einen Wert zwischen $1\hspace{0.05cm}\rm V$ und $2\hspace{0.05cm}\rm V$. Der Mittelwert beträgt $1.5\hspace{0.05cm}\rm V$).
- Dagegen ist bei $t = T_0/4$ der Signalwert des gesamten Ensembles identisch $0$. Das heißt: Bereits der lineare Mittelwert erfüllt die Bedingung der Stationarität nicht; der Prozess $\{x_i(t)\}$ ist nicht stationär und kann deshalb auch nicht ergodisch sein.
- Dagegen sind beim Prozess $\{y_i(t)\}$ aufgrund der gleichverteilten Phase zu allen Zeitpunkten die gleichen Momente zu erwarten ⇒ der Prozess ist stationär.
- Da bei der AKF-Berechnung die Phasenbeziehungen verloren gehen, steht jede einzelne Musterfunktion stellvertretend für den gesamten Prozess. Deshalb kann hier hypothetisch von Ergodizität ausgegangen werden. Am Ende der Aufgabe ist zu überprüfen, ob diese Annahme gerechtfertigt ist.
(2) Aufgrund der Ergodizität kann jede Musterfunktion zur AKF-Berechung herangezogen werden. Wir benutzen hier willkürlich die Phase $\varphi_i = 0$. Aufgrund der Periodizität genügt die Mitteilung über nur eine Periodendauer $T_0$. Dann gilt:
- $$\varphi_y (\tau) = \frac{1}{T_0} \cdot \int_0^{T_0} y(t) \cdot y (t+\tau) \hspace{0.1cm}{\rm d} t = \frac{{ x}_0^2}{{ T}_0} \cdot \int_0^{{\it T}_0} \cos (2 \pi {f_{\rm 0} t}) \cdot \cos (2 \pi {f_{\rm 0} (t+\tau)}) \hspace{0.1cm}\rm d \it t.$$
Mit der trigonometrischen Beziehung
- $$\cos (\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \cos (\alpha + \beta) + {1}/{2} \cdot \cos (\alpha - \beta)$$
folgt daraus weiter:
- $$\varphi_y (\tau) = \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (4 \pi \it{f_{\rm 0} t} + {\rm 2} \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t + \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (-2 \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t. $$
Das erste Integral ist $0$ (Integration über zwei Perioden der Cosinusfunktion), der zweite Integrand ist unabhängig von der Integrationsvariablen $t$. Daraus folgt: $\varphi_y (\tau) ={{ x}_0^2}/{\rm 2} \cdot \cos (2 \pi {f_{\rm 0} \tau}). $ Für die angegebenen Zeitpunkte gilt mit $x_0 = 2\hspace{0.05cm}\rm V$:
- $$\varphi_y (0)\hspace{0.15cm}\underline{ = 2\hspace{0.05cm}{\rm V}^2}, \hspace{0.5cm} \varphi_y (0.25 \cdot { T}_{\rm 0}{\rm )} \hspace{0.15cm}\underline{ = 0}, \hspace{0.5cm} \varphi_y (\rm 1.5 \cdot {\it T}_{\rm 0} {\rm )} \hspace{0.15cm}\underline{= \rm -2\hspace{0.05cm}{\rm V}^2}.$$
(3) Richtig ist nur der erste Lösungsvorschlag:
- Der Mittelwert $m_y$ kann aus dem Grenzwert der AKF für $\tau \to \infty$ ermittelt werden, wenn man die periodischen Anteile ausschließt. Daraus folgt $m_y= 0$.
- Die Varianz (Leistung) ist gleich dem AKF-Wert an der Stelle $\tau = 0$, also $2\hspace{0.05cm}\rm V^2$. Der Effektivwert ist die Quadratwurzel daraus: $\sigma_y \approx 1.414\hspace{0.05cm}\rm V$.
- Die Periodendauer eines periodischen Zufallsprozesses bleibt in der AKF erhalten, das heißt, auch die Periodendauer der AKF beträgt $T_0$.