Aufgaben:Aufgabe 3.9: Faltung von Rechteck und Gauß: Unterschied zwischen den Versionen
| (19 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
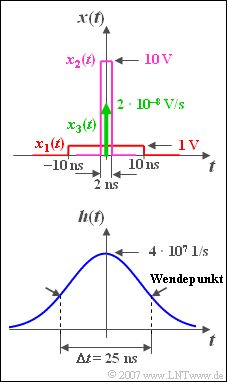
| − | [[Datei:P_ID540__Sig_A_3_9_neu.png|250px|right| | + | [[Datei:P_ID540__Sig_A_3_9_neu.png|250px|right|frame|Rechteckförmiges $x(t)$ und gaußförmiges $h(t)$]] |
| − | Wir betrachten | + | Wir betrachten einen gaußförmigen Tiefpass mit der äquivalenten Bandbreite $\Delta f = 40 \,\text{MHz}$: |
| − | $$H( f ) = {\rm{e}}^{{\rm{ - \pi }}( {f/\Delta f} )^2 } .$$ | + | :$$H( f ) = {\rm{e}}^{{\rm{ - \pi }}( {f/\Delta f} )^2 } .$$ |
Die dazugehörige Impulsantwort lautet: | Die dazugehörige Impulsantwort lautet: | ||
| − | $$h( t ) = \Delta f \cdot {\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm} \cdot \hspace{0.05cm} t} )^2 } .$$ | + | :$$h( t ) = \Delta f \cdot {\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm} \cdot \hspace{0.05cm} t} )^2 } .$$ |
| − | Aus der Skizze ist zu ersehen, dass die äquivalente Zeitdauer ⇒ $\Delta t = 1/\Delta f = 25\,\text{ns}$ der Impulsantwort $h(t)$ an den beiden Wendepunkten der Gaußfunktion abgelesen werden kann. | + | Aus der Skizze ist zu ersehen, dass die äquivalente Zeitdauer ⇒ $\Delta t = 1/\Delta f = 25\,\text{ns}$ der Impulsantwort $h(t)$ an den beiden Wendepunkten der Gaußfunktion abgelesen werden kann. |
An den Eingang des Tiefpasses werden nun drei verschiedene impulsartige Signale angelegt: | An den Eingang des Tiefpasses werden nun drei verschiedene impulsartige Signale angelegt: | ||
| − | * ein Rechteckimpuls $x_1(t)$ mit | + | * ein Rechteckimpuls $x_1(t)$ mit Amplitude $A_1 =1\,\text{V}$ und Dauer $T_1 = 20\,\text{ns}$ (roter Verlauf), |
| − | * ein Rechteckimpuls $x_2(t)$ mit | + | * ein Rechteckimpuls $x_2(t)$ mit Amplitude $A_2 =10\,\text{V}$ und Dauer $T_2 = 2\,\text{ns}$ (violetter Verlauf), |
| − | * ein Diracimpuls $x_3(t)$ mit dem Impulsgewicht $2 \cdot 10^{–8} | + | * ein Diracimpuls $x_3(t)$ mit dem Impulsgewicht $2 \cdot 10^{–8}\text{ Vs}$ (grüner Pfeil). |
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltungssatz und Faltungsoperation]]. | + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltungssatz und Faltungsoperation]]. |
| − | *Sie | + | |
| − | + | *Zur Beantwortung der Fragen können Sie das komplementäre Gaußsche Fehlerintegral benutzen, das wie folgt definiert ist: | |
| − | + | [[Datei:P_ID541__Sig_A_3_9Tab_neu.png|right|frame|Einige Werte der Q-Funktion]] | |
| + | :$${\rm Q}( x ) = \frac{1}{ {\sqrt {2{\rm{\pi }}} }}\int_{\it x}^\infty {{\rm{e}}^{{{ - {\it u}}}^{\rm{2}} {\rm{/2}}} }\hspace{0.1cm}{\rm{d}}{\it u}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | + | Nebenstehende Tabelle gibt einige Funktionswerte wieder. | |
| + | <br clear=all> | ||
| + | |||
| − | |||
| Zeile 39: | Zeile 42: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie das Signal $y_1(t) = x_1(t) \ast h(t)$. Welche Werte ergeben sich zu den Zeiten $t | + | {Berechnen Sie das Signal $y_1(t) = x_1(t) \ast h(t)$. Welche Werte ergeben sich zu den Zeiten $t = 0$ und $t = 20\,\text{ns}$ mit der Näherung $(2\pi )^{1/2} \approx 2.5$? |
|type="{}"} | |type="{}"} | ||
| − | $y_1(t=0) =$ { 0.682 3% } V | + | $y_1(t=0)\ = \ $ { 0.682 3% } $\text{V}$ |
| − | $y_1(t=20\text{ns}) =$ { 0.158 3% } V | + | $y_1(t=20\,\text{ns})\ = \ $ { 0.158 3% } $\text{V}$ |
| − | {Welche Signalwerte ergeben sich beim Ausgangssignal $y_2(t) = x_2(t) \ast h(t)$ zu den Zeitpunkten | + | {Welche Signalwerte ergeben sich beim Ausgangssignal $y_2(t) = x_2(t) \ast h(t)$ zu den betrachteten Zeitpunkten? |
|type="{}"} | |type="{}"} | ||
| − | $y_2(t=0) =$ { 0.8 3% } V | + | $y_2(t=0)\ = \ $ { 0.8 3% } $\text{V}$ |
| − | $y_2(t=20\text{ns}) =$ { 0.11 3% } V | + | $y_2(t=20 \,\text{ns})\ = \ $ { 0.11 3% } $\text{V}$ |
| − | {Wie groß ist das Ausgangssignal $y_3(t) = x_3(t) \ast h(t)$ zu den betrachteten Zeitpunkten? Interpretieren Sie das Ergebnis. | + | {Wie groß ist das Ausgangssignal $y_3(t) = x_3(t) \ast h(t)$ zu den betrachteten Zeitpunkten? Interpretieren Sie das Ergebnis. |
|type="{}"} | |type="{}"} | ||
| − | $y_3(t=0) =$ { 0.8 3% } V | + | $y_3(t=0)\ = \ $ { 0.8 3% } $\text{V}$ |
| − | $y_3(t=20\text{ns}) =$ { 0.11 3% } V | + | $y_3(t=20\, \text{ns})\ = \ $ { 0.11 3% } $\text{V}$ |
| Zeile 60: | Zeile 63: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Das Faltungsintegral lautet hier: |
| − | |||
| − | |||
| − | + | :$$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{A_1 }{\sqrt{2\pi }} \cdot\int_{u_1 }^{u_2 } {{\rm{e}}^{ - u^2 /2}\hspace{0.1cm} {\rm{d}}u.}$$ | |
| − | + | *Hierbei wurde die Substitution $u = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \tau$ verwendet. Die Integrationsgrenzen liegen bei: | |
| − | |||
| − | Die Integrationsgrenzen liegen bei: | ||
| − | $$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \ | + | :$$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t - T_1 /2} \big),\hspace{0.5cm}u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t + T_1 /2} \big).$$ |
| − | + | *Mit dem komplementären Gaußschen Fehlerintegral kann hierfür auch geschrieben werden: | |
| − | |||
| − | Mit dem komplementären Gaußschen Fehlerintegral kann hierfür auch geschrieben werden: | ||
| − | $$y_1 (t) = A_1 \cdot \ | + | :$$y_1 (t) = A_1 \cdot \big[ {{\rm Q} ( {u_1 } ) - {\rm Q}( {u_2 } )} \big].$$ |
| − | Für den Zeitpunkt $t = 0$ erhält man mit $(2\pi )1/2 \approx 2.5$: | + | *Für den Zeitpunkt $t = 0$ erhält man mit $(2\pi )^{1/2} \approx 2.5$: |
| − | $$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$ | + | :$$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$ |
| − | Mit $u_1 = | + | *Mit $u_1 = -u_2 = -1$ folgt für die beiden gesuchten Signalwerte: |
| − | $$y_1 ( {t = 0} ) \approx A_1 \cdot \ | + | :$$y_1 ( {t = 0} ) \approx A_1 \cdot \big[ {{\rm Q}( { - 1} ) - {\rm Q}(+ 1 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.841 - 0}}{\rm{.159}}} \big] \hspace{0.15 cm}\underline{= 0.682\;{\rm{V}}}{\rm{,}}$$ |
| + | :$$y_1 ( {t = 20\;{\rm{ns}}} ) \approx A_1 \cdot \big[ {{\rm Q}( 1 ) - {\rm Q}( 3 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.159 - 0}}{\rm{.001}}} \big] \hspace{0.15 cm}\underline{= 0.158\;{\rm{V}}}{\rm{.}}$$ | ||
| − | |||
| − | |||
| − | |||
| − | '''2 | + | '''(2)''' Analog zur ersten Musterlösung erhält man für den schmaleren Eingangsimpuls $x_2(t)$: |
| − | $$y_2 ( {t = 0} ) \approx A_2 \cdot \ | + | :$$y_2 ( {t = 0} ) \approx A_2 \cdot \big[ {{\rm Q}( { - 0.1} ) - {\rm Q}( {0.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.540 - 0}}{\rm{.460}}} \big] \hspace{0.15 cm}\underline{= 0.80\;{\rm{V}}}{\rm{,}}$$ |
| − | $$y_2 ( {t = 20\,{\rm ns}} ) \approx A_2 \cdot \ | + | :$$y_2 ( {t = 20\,{\rm ns}} ) \approx A_2 \cdot \big[ {{\rm Q}( {1.9} ) - {\rm Q}( {2.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.029 - 0}}{\rm{.018}}} \big] \hspace{0.15 cm}\underline{= 0.11\;{\rm{V}}}{\rm{.}}$$ |
| − | '''3 | + | |
| + | '''(3)''' Beim diracförmigen Eingangssignal $x_3(t)$ ist das Ausgangssignal $y_3(t)$ gleich der Impulsantwort $h(t)$, gewichtet mit dem Gewicht der Diracfunktion: | ||
| − | $$y_3 (t) = 2 \cdot 10^{ - 8} \,{\rm{Vs}} \cdot 4 \cdot 10^7 \;{\rm{1/s}} \cdot {\rm{e}}^{ - {\rm{\pi }}( {\Delta f \cdot t})^2 }.$$ | + | :$$y_3 (t) = 2 \cdot 10^{ - 8} \,{\rm{Vs}} \cdot 4 \cdot 10^7 \;{\rm{1/s}} \cdot {\rm{e}}^{ - {\rm{\pi }}( {\Delta f \cdot t})^2 }.$$ |
| + | |||
| + | *Zum Zeitpunkt $t = 0$ erhält man auch hier mit guter Näherung $y_3( t=0)\hspace{0.15 cm}\underline{ =0.8\, {\rm V}}$. | ||
| + | *Nach $20\, \rm ns$ ist der Ausgangsimpuls um den Faktor ${\rm e}^{–0.64π} \hspace{0.15 cm}\underline{\approx 0.136}$ kleiner und man erhält $y_3( t = 20 \,\text{ns}) ≈ 0.11 \,\text{V}$. | ||
| + | |||
| − | + | Man erkennt aus dem Vergleich der Resultate aus '''(2)''' und '''(3)''', dass $y_3(t) \approx y_2(t)$ gilt. | |
| − | Man erkennt aus dem Vergleich der Resultate aus 2) und 3), dass $y_3(t) | + | *Der Grund hierfür ist, dass der Diracimpuls eine gute Näherung für einen rechteckförmigen Eingangsimpuls gleicher Fläche ist, wenn die Rechteckdauer $T$ deutlich kleiner als die äquivalente Impulsdauer $\Delta t$ der Impulsantwort ist. |
| + | *Das heißt für unser Beispiel: Ist die Dauer $T$ des rechteckförmigen Eingangsimpulses $x(t)$ deutlich kleiner als die äquivalente Dauer $\Delta t$ der gaußförmigen Impulsantwort $h(t)$, dann ist auch der Ausgangsimpuls $y(t)$ nahezu gaußförmig. Aber: '''Gauß (einmal) gefaltet mit Nicht–Gauß ergibt nie (exakt) Gauß!''' | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | [[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | ||
Aktuelle Version vom 29. April 2021, 15:26 Uhr
Wir betrachten einen gaußförmigen Tiefpass mit der äquivalenten Bandbreite $\Delta f = 40 \,\text{MHz}$:
- $$H( f ) = {\rm{e}}^{{\rm{ - \pi }}( {f/\Delta f} )^2 } .$$
Die dazugehörige Impulsantwort lautet:
- $$h( t ) = \Delta f \cdot {\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm} \cdot \hspace{0.05cm} t} )^2 } .$$
Aus der Skizze ist zu ersehen, dass die äquivalente Zeitdauer ⇒ $\Delta t = 1/\Delta f = 25\,\text{ns}$ der Impulsantwort $h(t)$ an den beiden Wendepunkten der Gaußfunktion abgelesen werden kann.
An den Eingang des Tiefpasses werden nun drei verschiedene impulsartige Signale angelegt:
- ein Rechteckimpuls $x_1(t)$ mit Amplitude $A_1 =1\,\text{V}$ und Dauer $T_1 = 20\,\text{ns}$ (roter Verlauf),
- ein Rechteckimpuls $x_2(t)$ mit Amplitude $A_2 =10\,\text{V}$ und Dauer $T_2 = 2\,\text{ns}$ (violetter Verlauf),
- ein Diracimpuls $x_3(t)$ mit dem Impulsgewicht $2 \cdot 10^{–8}\text{ Vs}$ (grüner Pfeil).
Hinweise:
- Die Aufgabe gehört zum Kapitel Faltungssatz und Faltungsoperation.
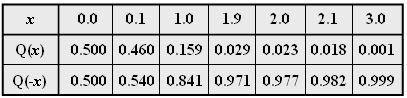
- Zur Beantwortung der Fragen können Sie das komplementäre Gaußsche Fehlerintegral benutzen, das wie folgt definiert ist:
- $${\rm Q}( x ) = \frac{1}{ {\sqrt {2{\rm{\pi }}} }}\int_{\it x}^\infty {{\rm{e}}^{{{ - {\it u}}}^{\rm{2}} {\rm{/2}}} }\hspace{0.1cm}{\rm{d}}{\it u}.$$
Nebenstehende Tabelle gibt einige Funktionswerte wieder.
Fragebogen
Musterlösung
- $$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{A_1 }{\sqrt{2\pi }} \cdot\int_{u_1 }^{u_2 } {{\rm{e}}^{ - u^2 /2}\hspace{0.1cm} {\rm{d}}u.}$$
- Hierbei wurde die Substitution $u = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \tau$ verwendet. Die Integrationsgrenzen liegen bei:
- $$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t - T_1 /2} \big),\hspace{0.5cm}u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t + T_1 /2} \big).$$
- Mit dem komplementären Gaußschen Fehlerintegral kann hierfür auch geschrieben werden:
- $$y_1 (t) = A_1 \cdot \big[ {{\rm Q} ( {u_1 } ) - {\rm Q}( {u_2 } )} \big].$$
- Für den Zeitpunkt $t = 0$ erhält man mit $(2\pi )^{1/2} \approx 2.5$:
- $$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$
- Mit $u_1 = -u_2 = -1$ folgt für die beiden gesuchten Signalwerte:
- $$y_1 ( {t = 0} ) \approx A_1 \cdot \big[ {{\rm Q}( { - 1} ) - {\rm Q}(+ 1 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.841 - 0}}{\rm{.159}}} \big] \hspace{0.15 cm}\underline{= 0.682\;{\rm{V}}}{\rm{,}}$$
- $$y_1 ( {t = 20\;{\rm{ns}}} ) \approx A_1 \cdot \big[ {{\rm Q}( 1 ) - {\rm Q}( 3 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.159 - 0}}{\rm{.001}}} \big] \hspace{0.15 cm}\underline{= 0.158\;{\rm{V}}}{\rm{.}}$$
(2) Analog zur ersten Musterlösung erhält man für den schmaleren Eingangsimpuls $x_2(t)$:
- $$y_2 ( {t = 0} ) \approx A_2 \cdot \big[ {{\rm Q}( { - 0.1} ) - {\rm Q}( {0.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.540 - 0}}{\rm{.460}}} \big] \hspace{0.15 cm}\underline{= 0.80\;{\rm{V}}}{\rm{,}}$$
- $$y_2 ( {t = 20\,{\rm ns}} ) \approx A_2 \cdot \big[ {{\rm Q}( {1.9} ) - {\rm Q}( {2.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.029 - 0}}{\rm{.018}}} \big] \hspace{0.15 cm}\underline{= 0.11\;{\rm{V}}}{\rm{.}}$$
(3) Beim diracförmigen Eingangssignal $x_3(t)$ ist das Ausgangssignal $y_3(t)$ gleich der Impulsantwort $h(t)$, gewichtet mit dem Gewicht der Diracfunktion:
- $$y_3 (t) = 2 \cdot 10^{ - 8} \,{\rm{Vs}} \cdot 4 \cdot 10^7 \;{\rm{1/s}} \cdot {\rm{e}}^{ - {\rm{\pi }}( {\Delta f \cdot t})^2 }.$$
- Zum Zeitpunkt $t = 0$ erhält man auch hier mit guter Näherung $y_3( t=0)\hspace{0.15 cm}\underline{ =0.8\, {\rm V}}$.
- Nach $20\, \rm ns$ ist der Ausgangsimpuls um den Faktor ${\rm e}^{–0.64π} \hspace{0.15 cm}\underline{\approx 0.136}$ kleiner und man erhält $y_3( t = 20 \,\text{ns}) ≈ 0.11 \,\text{V}$.
Man erkennt aus dem Vergleich der Resultate aus (2) und (3), dass $y_3(t) \approx y_2(t)$ gilt.
- Der Grund hierfür ist, dass der Diracimpuls eine gute Näherung für einen rechteckförmigen Eingangsimpuls gleicher Fläche ist, wenn die Rechteckdauer $T$ deutlich kleiner als die äquivalente Impulsdauer $\Delta t$ der Impulsantwort ist.
- Das heißt für unser Beispiel: Ist die Dauer $T$ des rechteckförmigen Eingangsimpulses $x(t)$ deutlich kleiner als die äquivalente Dauer $\Delta t$ der gaußförmigen Impulsantwort $h(t)$, dann ist auch der Ausgangsimpuls $y(t)$ nahezu gaußförmig. Aber: Gauß (einmal) gefaltet mit Nicht–Gauß ergibt nie (exakt) Gauß!