Aufgaben:Aufgabe 3.6: Transversalfilter des Optimalen Nyquistentzerrers

• Zurück zum Buch

Transversalfilter des
Optimalen Nyquistentzerrers

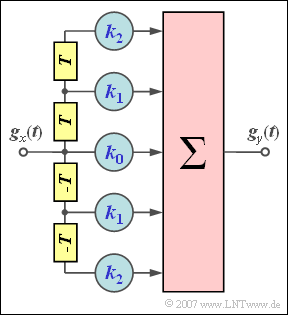
Am Eingang des in der Grafik gezeigten symmetrischen Transversalfilters zweiter Ordnung  $(N = 2)$  liegt ein Dreieckimpuls (auf $1$ normiert):

$$g_x(t) = \left\{ \begin{array}{c} 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{(2T)} \\ \\ 0 \\ \end{array} \right. \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}|\hspace{0.05cm}t\hspace{0.05cm}| \le 2\hspace{0.05cm}T, \\ \\ |\hspace{0.05cm}t\hspace{0.05cm}| \ge 2\hspace{0.05cm}T. \\ \end{array}$$

Sind alle Filterkoeffizienten  $k_0$,  $k_1$  und  $k_2$  ungleich Null, so gilt für den Impuls am Ausgang:

$$g_y(t) \ = k_0 \cdot g_x(t) + k_1 \cdot \big[ g_x(t-T)+ g_x(t+T) \big] + k_2 \cdot \big[ g_x(t-2T)+ g_x(t+2T) \big]\hspace{0.05cm}.$$

Durch geeignete Wahl der Filterkoeffizienten  $k_0$,  $k_1$  und  $k_2$  kann der Ausgangsimpuls folgende Bedingungen erfüllen:

$$g_0 = g_y(t = 0) = 1,\hspace{0.2cm}g_1 = g_y(t = \pm T) = 0,\hspace{0.2cm}g_2 = g_y(t = \pm 2 T) = 0 \hspace{0.05cm}.$$

• Ein Filter erster Ordnung  $(N = 1)$  ergibt sich aus obiger Anordnung und Gleichung, indem man den Koeffizienten  $k_2 = 0$  setzt.
• Durch geeignete Wahl von  $k_0$  und  $k_1$  kann dann  $g_0 = 1$  und  $g_1 = 0$  erreicht werden. Allerdings wird in diesem Fall stets  $g_2 ≠ 0$  sein.

Hinweis:

• Die Aufgabe gehört zum Kapitel  Linare Nyquistentzerrung.

Fragebogen

1

Wie lauten die optimalen Koeffizienten für das Filter erster Ordnung   ⇒   $k_2 = 0$?

$k_0\ = \ $

$k_1\ = \ $

2

Wie groß sind die Ausgangswerte zu den Zeitpunkten  $t = 2T$  und  $t = 3T$?

$g_2\ = \ $

$g_3\ = \ $

3

Wie lauten die optimalen Koeffizienten für das Filter zweiter Ordnung  $(N = 2)$?

$k_0\ = \ $

$k_1\ = \ $

$k_2\ = \ $

4

Wie groß sind die Ausgangswerte zu den Zeitpunkten  $t = 3T$  und  $t = 4T$?

$g_3\ = \ $

$g_4\ = \ $

Musterlösung

Musterlösung

(1)  Der Eingangsimpuls $g_x(t)$ ist durch folgende Abtastwerte bei Vielfachen von $T$ gegeben:

$$g_x(t = 0) = 1,\hspace{0.2cm}g_x(t = \pm T) = 0.5,\hspace{0.2cm}g_x(t = \pm 2 T) = ... = 0 \hspace{0.05cm}.$$

Damit kann folgendes Gleichungssystem aufgestellt werden:

$$t = 0\hspace{-0.1cm}:\hspace{0.2cm}g_0 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} k_0 \cdot 1.0 + k_1 \cdot 2 \cdot 0.5 = 1\hspace{0.05cm},$$

$$t = T\hspace{-0.1cm}:\hspace{0.2cm}g_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} k_0 \cdot 0.5 + k_1 \cdot 1.0 = 0 \hspace{0.05cm}.$$

Aus diesen Gleichungen folgt $k_0 \ \underline {= \ 2}$ und $k_1 \ \underline {= \ –1}$.

Ausgangsimpuls für N = 1

(2)  Die Werte $g_0 = 1$ und $g_1 = 0$ wurden bereits der Optimierung zugrundegelegt und sind deshalb unbestritten. Zum Zeitpunkt $t = 2T$ ergibt sich am Ausgang, wobei $k_{-1} = k_1 = -1$ zu berücksichtigen ist:

$$g_2 = g_y(t = 2 T) = g_x(t = T) \cdot k_{-1}\hspace{0.15cm}\underline { = -0.5 = g_{-2}} \hspace{0.05cm}.$$

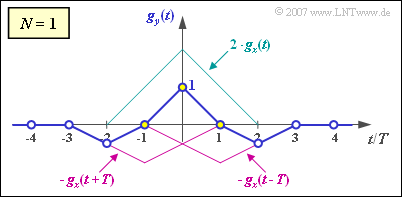
Da alle Eingangswerte zu den Zeiten $2T$, $3T$ und $4T$ Null sind, ist $g_3 = g_y(t = 3T) \underline {= \ 0}$. Damit ergibt sich der Ausgangsimpuls $g_y(t)$ gemäß Skizze.

Ausgangsimpuls für N = 2

(3)  Bei einem Filter zweiter Ordnung lautet das Gleichungssystem:

$$t = 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_1 \cdot 0.5 + k_2 \cdot 1.0 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} k_2 = - 0.5 \cdot k_1\hspace{0.05cm},$$

$$t = T\hspace{-0.1cm}:\hspace{0.2cm}g_1= k_0 \cdot 0.5 +k_1 \cdot 1.0 + k_2 \cdot 0.5 = 0\hspace{0.05cm},$$

$$\hspace{7.3cm}\Rightarrow \hspace{0.3cm} k_1 = - {2}/{3} \cdot k_0\hspace{0.05cm},$$

$$t = 0\hspace{-0.1cm}:\hspace{0.2cm}g_0 = k_0 \cdot 1.0 + k_1 \cdot 0.5 + k_1 \cdot 0.5 = 1\hspace{0.05cm},$$

$$\hspace{7.3cm}\Rightarrow \hspace{0.3cm} k_0 = 3 \hspace{0.05cm}.$$

Damit sind die optimalen Koeffizienten $k_0 \ \underline {= \ 3},$ $k_1 \ \underline {= \ –2}$, $k_2 \ \underline {= \ 1}.$
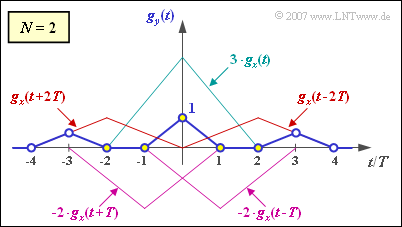
(4)  Bei analoger Vorgehensweise wie in der Teilaufgabe (2) erhält man $g_4 \ \underline {= \ 0}$ sowie

$$g_3 = g_y(t = 3 T) = g_x(t = T) \cdot k_{-2} = 0.5 \cdot 1 \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$

Die beiden Grafiken zeigen allerdings auch, dass bei der hier vorliegenden Dreickform die optimale Nyquistentzerrung keine Verbesserung bringt. Das Auge ist in allen Fällen gerade geschlossen:

$$N = 0\hspace{-0.1cm}:\hspace{0.2cm} \ddot{o}/2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} g_0 - 2 \cdot g_1 = 1- 2 \cdot 0.5 = 0 \hspace{0.05cm}, $$

$$N = 1\hspace{-0.1cm}:\hspace{0.2cm} \ddot{o}/2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} g_0 - 2 \cdot |g_2 | = 1- 2 \cdot 0.5 = 0 \hspace{0.05cm}, $$

$$N = 2\hspace{-0.1cm}:\hspace{0.2cm} \ddot{o}/2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} g_0 - 2 \cdot g_3 = 1- 2 \cdot 0.5 = 0 \hspace{0.05cm}.$$