Aufgaben:Aufgabe 3.6: Transversalfilter des Optimalen Nyquistentzerrers: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1432__Dig_A_3_6.png|right|frame]] |
| + | Am Eingang des in der Grafik gezeigten symmetrischen Transversalfilters zweiter Ordnung ($N = 2$) liegt ein Dreieckimpuls (auf 1 normiert): | ||
| + | :$$g_x(t) = \left\{ \begin{array}{c} 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{(2T)} \\ | ||
| + | \\ 0 \\ \end{array} \right. | ||
| + | \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ {\rm{f\ddot{u}r}} \\ \end{array} | ||
| + | \begin{array}{*{20}c}|\hspace{0.05cm}t\hspace{0.05cm}| \le 2\hspace{0.05cm}T, \\ \\ |\hspace{0.05cm}t\hspace{0.05cm}| \ge 2\hspace{0.05cm}T. \\ | ||
| + | \end{array}$$ | ||
| + | |||
| + | Sind alle Filterkoeffizienten $k_0$, $k_1$ und $k_2$ ungleich $0$, so gilt für den Impuls am Ausgang: | ||
| + | :$$g_y(t) & = & k_0 \cdot g_x(t) + \\ & + & k_1 \cdot [ g_x(t-T)+ | ||
| + | g_x(t+T) ]+ \\ & + & k_2 \cdot [ g_x(t-2T)+ g_x(t+2T) | ||
| + | ]\hspace{0.05cm}.$$ | ||
| + | |||
| + | Durch geeignete Wahl der Filterkoeffizienten $k_0$, $k_1$ und $k_2$ gelingt es, dass der Ausgangsimpuls folgende Bedingungen erfüllt: | ||
| + | :$$g_0 = g_y(t = 0) = 1,\hspace{0.2cm}g_1 = g_y(t = \pm T) = | ||
| + | 0,\hspace{0.2cm}g_2 = g_y(t = \pm 2 T) = 0 \hspace{0.05cm}.$$ | ||
| + | |||
| + | Ein Filter erster Ordnung ($N = 1$) ergibt sich aus obiger Anordnung und Gleichung, indem man den Koeffizienten $k_2 = 0$ setzt. Durch geeignete Wahl von $k_0$ und $k_1$ kann dann $g_0 = 1$ und $g_1 = 0$ erreicht werden. Allerdings wird in diesem Fall stets $g_2 ≠ 0$ sein. | ||
| + | |||
| + | ''Hinweis:'' Die Aufgabe bezieht sich auf den Lehrstoff von [[Digitalsignal%C3%BCbertragung/Lineare_Nyquistentzerrung|Kapitel 3.5]]. | ||
Version vom 25. Oktober 2017, 14:37 Uhr
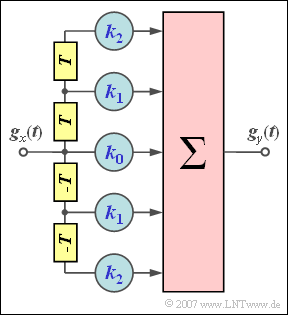
Am Eingang des in der Grafik gezeigten symmetrischen Transversalfilters zweiter Ordnung ($N = 2$) liegt ein Dreieckimpuls (auf 1 normiert):
- $$g_x(t) = \left\{ \begin{array}{c} 1 - {|\hspace{0.05cm}t\hspace{0.05cm}|}/{(2T)} \\ \\ 0 \\ \end{array} \right. \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}|\hspace{0.05cm}t\hspace{0.05cm}| \le 2\hspace{0.05cm}T, \\ \\ |\hspace{0.05cm}t\hspace{0.05cm}| \ge 2\hspace{0.05cm}T. \\ \end{array}$$
Sind alle Filterkoeffizienten $k_0$, $k_1$ und $k_2$ ungleich $0$, so gilt für den Impuls am Ausgang:
- $$g_y(t) & = & k_0 \cdot g_x(t) + \\ & + & k_1 \cdot [ g_x(t-T)+ g_x(t+T) ]+ \\ & + & k_2 \cdot [ g_x(t-2T)+ g_x(t+2T) ]\hspace{0.05cm}.$$
Durch geeignete Wahl der Filterkoeffizienten $k_0$, $k_1$ und $k_2$ gelingt es, dass der Ausgangsimpuls folgende Bedingungen erfüllt:
- $$g_0 = g_y(t = 0) = 1,\hspace{0.2cm}g_1 = g_y(t = \pm T) = 0,\hspace{0.2cm}g_2 = g_y(t = \pm 2 T) = 0 \hspace{0.05cm}.$$
Ein Filter erster Ordnung ($N = 1$) ergibt sich aus obiger Anordnung und Gleichung, indem man den Koeffizienten $k_2 = 0$ setzt. Durch geeignete Wahl von $k_0$ und $k_1$ kann dann $g_0 = 1$ und $g_1 = 0$ erreicht werden. Allerdings wird in diesem Fall stets $g_2 ≠ 0$ sein.
Hinweis: Die Aufgabe bezieht sich auf den Lehrstoff von Kapitel 3.5.
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.