Aufgabe 3.5Z: Nochmals Kullback-Leibler-Distanz
Die Wahrscheinlichkeitsfunktion lautet:
- $$P_X(X) = \big[\hspace{0.03cm}0.25\hspace{0.03cm}, \hspace{0.03cm} 0.25\hspace{0.03cm},\hspace{0.03cm} 0.25 \hspace{0.03cm}, \hspace{0.03cm} 0.25\hspace{0.03cm}\big]\hspace{0.05cm}.$$
Die Zufallsgröße $X$ ist also gekennzeichnet durch
- den Symbolumfang $M=4$,
- gleiche Wahrscheinlichkeiten $P_X(1) = P_X(2) = P_X(3) = P_X(4) = 1/4$ .
Die Zufallsgröße $Y$ ist stets eine Näherung für $X$:
- Sie wurde per Simulation aus einer Gleichverteilung gewonnen, wobei jeweils nur $N$ Zufallswerte ausgewertet wurden.
- Das heißt: $P_Y(1)$, ... , $P_Y(4)$ sind im herkömmlichen Sinn keine Wahrscheinlichkeiten. Sie beschreiben vielmehr relative Häufigkeiten.
Das Ergebnis der sechsten Versuchsreihe (mit $N=1000$) wird demnach durch die folgende Wahrscheinlichkeitsfunktion zusammengefasst:
- $$P_Y(X) = \big [\hspace{0.05cm}0.225\hspace{0.05cm}, \hspace{0.05cm} 0.253\hspace{0.05cm},\hspace{0.05cm} 0.250 \hspace{0.05cm}, \hspace{0.05cm} 0.272\hspace{0.05cm}\big] \hspace{0.05cm}.$$
Bei dieser Schreibweise ist bereits berücksichtigt, dass die Zufallsgrößen $X$ und $Y$ auf dem gleichen Alphabet $X = \{1, 2, 3, 4\}$ basieren.
Mit diesen Voraussetzungen gilt für die relative Entropie (englisch: Informational Divergence) zwischen den beiden Wahrscheinlichkeitsfunktionen $P_X(.)$ und $P_Y(.)$ :
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = {\rm E}_X \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm}.$$
Man bezeichnet $D( P_X\hspace{0.05cm} || \hspace{0.05cm}P_Y)$ als (erste) Kullback–Leibler–Distanz.
- Diese ist ein Maß für die Ähnlichkeit zwischen den beiden Wahrscheinlichkeitsfunktionen $P_X(.)$ und $P_Y(.)$.
- Die Erwartungswertbildung geschieht hier hinsichtlich der (tatsächlich gleichverteilten) Zufallsgröße $X$. Dies wird durch die Nomenklatur ${\rm E}_X\big[.\big]$ angedeutet.
Eine zweite Form der Kullback–Leibler–Distanz ergibt sich durch die Erwartungswertbildung hinsichtlich der Zufallsgröße $Y$ ⇒ ${\rm E}_Y\big [.\big ]$:
- $$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) = {\rm E}_Y \hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^M P_Y(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y(\mu)}{P_X(\mu)} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Vorbemerkungen zu den 2D-Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seite Relative Entropie – Kullback-Leibler-Distanz.
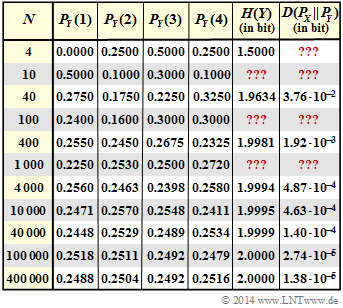
- Die Angaben der Entropie $H(Y)$ und der Kullback–Leibler–Distanz $D( P_X \hspace{0.05cm}|| \hspace{0.05cm}P_Y)$ in obiger Grafik sind in „bit” zu verstehen.
- Die in der Grafik mit „???" versehenen Felder sollen von Ihnen in dieser Aufgabe ergänzt werden.
Fragebogen
Musterlösung
(1) Bei gleichen Wahrscheinlichkeiten gilt mit $M = 4$: $H(X) = {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm} \underline {= 2\,{\rm (bit)}} \hspace{0.05cm}.$
(2) Die Wahrscheinlichkeiten für die empirisch ermittelten Zufallsgrößen $Y$ weichen im Allgemeinen (nicht immer!) von der Gleichverteilung um so mehr ab, je kleiner der Parameter $N$ ist. Man erhält
- $N = 1000 \Rightarrow P_Y(Y) = [0.225, 0.253, 0.250, 0.272]$:
- $$H(Y) \hspace{-0.15cm} = \hspace{-0.15cm} 0.225 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.225} + 0.253 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.253} + 0.250 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.250} + 0.272 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.272} \hspace{0.15cm} \underline {= 1.9968\,{\rm (bit)}} \hspace{0.05cm},$$
- $N = 100\Rightarrow P_Y(Y) = [0.24, 0.16, 0.30, 0.30]$:
- $$H(Y) = ... \hspace{0.15cm} \underline {= 1.9410\,{\rm (bit)}} \hspace{0.05cm},$$
- $N = 10 \Rightarrow P_Y(Y) = [0.5, 0.1, 0.3, 0.1]$:
- $$H(Y) = ... \hspace{0.15cm} \underline {= 1.6855\,{\rm (bit)}} \hspace{0.05cm}.$$
(3) Die Gleichung für die gesuchte Kullback–Leibler–Distanz lautet:
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = \sum_{\mu = 1}^{4} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} = \frac{1/4}{{\rm lg} \hspace{0.1cm}(2)} \cdot \left [ {\rm lg} \hspace{0.1cm} \frac{0.25}{P_Y(1)} + \frac{0.25}{P_Y(2)} + \frac{0.25}{P_Y(3)} + \frac{0.25}{P_Y(4)} \right ] $$
- $$\Rightarrow \hspace{0.3cm} D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = \frac{1}{4 \cdot {\rm lg} \hspace{0.1cm}(2)} \cdot \left [ {\rm lg} \hspace{0.1cm} \frac{0.25^4}{P_Y(1) \cdot P_Y(2)\cdot P_Y(3)\cdot P_Y(4)} \right ] \hspace{0.05cm}.$$
Der Logarithmus zur Basis 2 ⇒ $\log_2(.)$ wurde zur einfachen Nutzung des Taschenrechners durch den Zehnerlogarithmus 2 ⇒ $\lg(.)$ ersetzt. Man erhält die folgenden numerischen Ergebnisse:
- für $N=1000$:
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = \frac{1}{4 \cdot {\rm lg} \hspace{0.1cm}(2)} \cdot \left [ {\rm lg} \hspace{0.1cm} \frac{0.25^4}{0.225 \cdot 0.253\cdot 0.250\cdot 0.272} \right ] \hspace{0.15cm} \underline {= 3.28 \cdot 10^{-3}\,{\rm (bit)}} \hspace{0.05cm},$$
- für $N=100$:
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = \frac{1}{4 \cdot {\rm lg} \hspace{0.1cm}(2)} \cdot \left [ {\rm lg} \hspace{0.1cm} \frac{0.25^4}{0.24 \cdot 0.16\cdot 0.30\cdot 0.30} \right ] \hspace{0.15cm} \underline {= 4.42 \cdot 10^{-2}\,{\rm (bit)}} \hspace{0.05cm},$$
- für $N=10$:
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = \frac{1}{4 \cdot {\rm lg} \hspace{0.1cm}(2)} \cdot \left [ {\rm lg} \hspace{0.1cm} \frac{0.25^4}{0.5 \cdot 0.1\cdot 0.3\cdot 0.1} \right ] \hspace{0.15cm} \underline {= 3.45 \cdot 10^{-1}\,{\rm (bit)}} \hspace{0.05cm}.$$
(4) Richtig ist Nein, wie am Beispiel $N = 100$ gezeigt werden soll:
- $$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) = \sum_{\mu = 1}^M P_Y(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y(\mu)}{P_X(\mu)} = 0.24\cdot {\rm log}_2 \hspace{0.1cm} \frac{0.24}{0.25} + 0.16\cdot {\rm log}_2 \hspace{0.1cm} \frac{0.16}{0.25} +2 \cdot 0.30\cdot {\rm log}_2 \hspace{0.1cm} \frac{0.30}{0.25} = 0.0407\,{\rm (bit)}\hspace{0.05cm}.$$
In der Teilaufgabe (c) haben wir stattdessen $D(P_X\hspace{0.05cm}|| \hspace{0.05cm} P_Y) = 0.0442$ erhalten. Das bedeutet auch: Der Name „Distanz” ist etwas irreführend. Danach würde man eigentlich $D(P_Y\hspace{0.05cm}|| \hspace{0.05cm} P_X)$ = $D(P_X\hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ erwarten.
(5) Mit $P_Y(X) = [0, 0.25, 0.5, 0.25]$ erhält man:
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = 0.25\cdot {\rm log}_2 \hspace{0.1cm} \frac{0.25}{0} + 2 \cdot 0.25\cdot {\rm log}_2 \hspace{0.1cm} \frac{0.25}{0.25}+0.25\cdot {\rm log}_2 \hspace{0.1cm} \frac{0.25}{0.50}\hspace{0.05cm}.$$
Aufgrund des ersten Terms ergibt sich für $D(P_X\hspace{0.05cm}|| \hspace{0.05cm}P_Y)$ ein unendlich großer Wert. Für die zweite Kullback–Leibler–Distanz gilt:
- $$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) = 0\cdot {\rm log}_2 \hspace{0.1cm} \frac{0}{0.25} + 2 \cdot 0.25\cdot {\rm log}_2 \hspace{0.1cm} \frac{0.25}{0.25}+ 0.50\cdot {\rm log}_2 \hspace{0.1cm} \frac{0.5}{0.25} \hspace{0.05cm}.$$
Nach einer Grenzwertbetrachtung erkennt man, dass der erste Term das Ergebnis $0$ liefert. Auch der zweite Term ergibt sich zu $0$, und man erhält als Endergebnis:
- $$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) = 0.50\cdot {\rm log}_2 \hspace{0.1cm} (2) \hspace{0.15cm} \underline {= 0.5\,{\rm (bit)}} \hspace{0.05cm}.$$
Richtig sind somit die Aussagen 3 und 5:
- Auch aus diesem Extrembeispiel wird deutlich, dass sich $D(P_Y\hspace{0.05cm}|| \hspace{0.05cm} P_X)$ stets von $D(P_X\hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ unterscheidet.
- Nur für den Sonderfall $P_Y = P_X$ sind beide Kullback–Leibler–Distanzen gleich, nämlich Null.
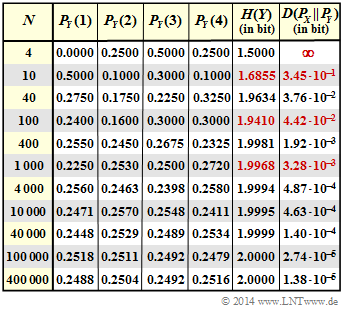
- Die nebenstehende Tabelle zeigt das vollständige Ergebnis dieser Aufgabe.
(6) Richtig ist Nein. Die Tendenz ist zwar eindeutig: Je größer $N$ ist,
- desto mehr nähert sich $H(Y)$ im Prinzip dem Endwert $H(X) = 2 \ \rm bit$ an.
- um so kleiner werden die Distanzen $D(P_X\hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ und $D(P_Y\hspace{0.05cm}|| \hspace{0.05cm} P_X)$.
Man erkennt aus der Tabelle aber auch, dass es Ausnahmen gibt:
- Die Entropie $H(Y)$ ist für $N = 1000$ kleiner als für $N = 400$,
- Die Distanz $D(P_X\hspace{0.05cm}|| \hspace{0.05cm}P_Y)$ ist für $N = 1000$ größer als für $N = 400$.
Der Grund hierfür ist, dass das hier dokumentierte empirische Experiment mit $N = 400$ eher zu einer Gleichverteilung geführt hat als das Experiment mit $N = 1000$.
Würde man dagegen sehr (unendlich) viele Versuche mit $N = 400$ und $N = 1000$ starten und über diese mitteln, ergäbe sich tatsächlich der eigentlich erwartete monotone Verlauf.