Aufgaben:Aufgabe 3.5: Schaltung mit R, L und C: Unterschied zwischen den Versionen
| (17 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1776__LZI_A_3_5.png|right|Vierpol mit R, L und C]] | + | [[Datei:P_ID1776__LZI_A_3_5.png|right|frame|Vierpol mit $R$, $L$ und $C$]] |
| − | Wir betrachten einen Vierpol mit dem Widerstand $R = 100 \ \rm Omega$ im Längszweig, während im Querzweig eine Induktivität $L$ und eine Kapazität $C$ in Serie geschaltet sind. Darunter gezeichnet ist das Pol–Nullstellen–Diagramm. | + | Wir betrachten einen Vierpol mit dem Widerstand $R = 100 \ \rm \Omega$ im Längszweig, während im Querzweig eine Induktivität $L$ und eine Kapazität $C$ in Serie geschaltet sind. Darunter gezeichnet ist das Pol–Nullstellen–Diagramm. |
| − | Beachten Sie die Normierung der komplexen Frequenz $p = {\rm j} \cdot 2 \pi f$ auf den Wert $1/T$ mit $T = 1 \ \rm | + | Beachten Sie die Normierung der komplexen Frequenz $p = {\rm j} \cdot 2 \pi f$ auf den Wert $1/T$ mit $T = 1 \ \rm µ s$. Dies hat zur Folge, dass zum Beispiel der Pol bei $-1$ in Realität bei $-10^6 \cdot \ \rm 1/s$ liegt. |
Zur Berechnung von Zeitfunktionen kann man den Residuensatz anwenden: | Zur Berechnung von Zeitfunktionen kann man den Residuensatz anwenden: | ||
| − | *Bei $N$ einfachen Polen setzt sich | + | *Bei $N$ einfachen Polen setzt sich der Ausgang $y(t)$ aus $N$ Eigenschwingungen ("Residuen") zusammen. |
| − | *Bei einem einfachen Pol bei $p_{{\rm x}i}$ für das das Residuum: | + | *Bei einem einfachen Pol bei $p_{{\rm x}i}$ gilt für das das Residuum: |
| − | $${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} | + | :$${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} |
\hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= | \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= | ||
Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p | Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p | ||
| Zeile 18: | Zeile 18: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | Dieser Ansatz funktioniert aber nur dann, wenn die Anzahl $Z$ der Nullstellen kleiner ist als $N$, in dieser Aufgabe beispielsweise dann, wenn die Sprungantwort $ | + | :Dieser Ansatz funktioniert aber nur dann, wenn die Anzahl $Z$ der Nullstellen kleiner ist als $N$, in dieser Aufgabe beispielsweise dann, wenn die Sprungantwort $\sigma(t)$ berechnet wird. In diesem Fall ist $Z = 2$ und $N = 3$, da zusätzlich die Sprungfunktion am Eingang durch $X_{\rm L}(p) = 1/p$ berücksichtigt werden muss. |
| − | Für die Berechnung der Impulsantwort $h(t)$ funktioniert diese Vorgehensweise wegen $Z = N =2$ nicht. Hier kann | + | *Für die Berechnung der Impulsantwort $h(t)$ funktioniert diese Vorgehensweise wegen $Z = N =2$ nicht. |
| + | *Hier kann man die Tatsache berücksichtigen, dass das Integral über die Impulsantwort $h(t)$ die Sprungantwort $\sigma(t)$ ergibt. | ||
| − | + | ||
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation|Laplace–Rücktransformation]]. | + | |
| − | + | ||
| + | Hinweis: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation|Laplace–Rücktransformation]]. | ||
| + | |||
| Zeile 33: | Zeile 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Funktion hat | + | {Welche Funktion hat der hier betrachtete Vierpol? Handelt es sich um |
| − | |type=" | + | |type="()"} |
- einen Tiefpass, | - einen Tiefpass, | ||
- einen Hochpass, | - einen Hochpass, | ||
| Zeile 41: | Zeile 45: | ||
| − | {Berechnen Sie | + | {Berechnen Sie $L$ und $C$ für die vorgegebene Pol–Nullstellen–Konfiguration. Berücksichtigen Sie den Normierungswert $1/T$ und den Widerstand $R = 100 \ \rm \Omega$. |
|type="{}"} | |type="{}"} | ||
| − | $L$ | + | $L \hspace{0.24cm} = \ $ { 20 3% } $\ \rm µ H$ |
| − | $C$ | + | $C \hspace{0.2cm} = \ $ { 12.5 3% } $\ \rm nF$ |
| − | {Berechnen Sie das Ausgangssignal | + | {Berechnen Sie das Ausgangssignal $y(t) = \sigma(t)$, wenn am Eingang eine Sprungfunktion $x(t) = \gamma(t)$ anliegt. Geben Sie die folgenden Signalwerte ein: |
|type="{}"} | |type="{}"} | ||
| − | $y(t = 0)$ | + | $y(t = 0) \ = \ $ { 1 3% } |
| − | $y(t = 0.5 \ | + | $y(t = 0.5 \ \rm µ s) \ = \ $ { 0.215 3% } |
| − | $y(t = 2 \ | + | $y(t = 2.0 \ \rm µ s) \ = \ $ { 0.775 3% } |
| − | $y(t = 5 \ | + | $y(t = 5.0 \ \rmµ s) \ = \ $ { 0.989 3% } |
| − | {Berechnen Sie die Impulsantwort | + | {Berechnen Sie die Impulsantwort $h(t)$, insbesondere für die Zeitpunkte $t = 0$ und $t = 1 \ \rm µ s$. Welche der folgenden Aussagen treffen zu? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $h(t)$ beinhaltet eine Diracfunktion bei $t = 0$. |
| − | - Der kontinuierliche Anteil von | + | - Der kontinuierliche Anteil von $h(t)$ ist im gesamten Bereich negativ. |
| − | + Der kontinuierliche Anteil von | + | + Der kontinuierliche Anteil von $h(t)$ besitzt ein Maximum. |
| Zeile 66: | Zeile 70: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Richtig ist der <u>Lösungsvorschlag 4</u>: | |
| + | *Bei extrem tiefen Frequenzen $(f \rightarrow 0)$ hat die Kapazität $C$ einen unendlich großen Widerstand und bei sehr hohen Frequenzen $(f \rightarrow \infty)$ die Induktivität $L$. | ||
| + | *In beiden Fällen gilt $Y(f) = X(f)$ ⇒ $H(f) = 1$. | ||
| + | *Bei der Resonanzfrequenz $f_0$ wirkt dagegen die LC–Serienschaltung als Kurzschluss und es gilt $H(f = f_0) = 0$. | ||
| + | *Daraus folgt allein aus dem Blockschaltbild: Es handelt sich um eine <u>Bandsperre</u>. | ||
| + | |||
| + | |||
| − | + | '''(2)''' Aus dem Pol–Nullstellen–Diagramm ergibt sich die folgende $p$–Übertragungsfunktion $($ohne den Normierungsfaktor $1/T)$: | |
:$$H_{\rm L}(p)= \frac {(p - {\rm j} \cdot 2)(p + {\rm j} \cdot | :$$H_{\rm L}(p)= \frac {(p - {\rm j} \cdot 2)(p + {\rm j} \cdot | ||
2)} {(p +1)(p +4 )}= \frac {p^2 +4} {p^2 + 5 \cdot p +4} | 2)} {(p +1)(p +4 )}= \frac {p^2 +4} {p^2 + 5 \cdot p +4} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | *Unter Berücksichtigung der Spannungsteilereigenschaften erhält man mit dem Blindwiderstand $p \cdot L$ der Induktivität und dem Blindwiderstand $1/(p \cdot C)$ der Kapazität für die Schaltung: | |
:$$H_{\rm L}(p)= \frac { p\cdot L +1/(pC) } | :$$H_{\rm L}(p)= \frac { p\cdot L +1/(pC) } | ||
{R + p \cdot L +1/(pC) }= \frac { p^2 +1/(pC) } | {R + p \cdot L +1/(pC) }= \frac { p^2 +1/(pC) } | ||
{p^2 + p \cdot {R}/{L} +1/(pC) }\hspace{0.05cm} .$$ | {p^2 + p \cdot {R}/{L} +1/(pC) }\hspace{0.05cm} .$$ | ||
| − | + | *Durch Vergleich erkennt man unter Berücksichtigung des Normierungsfaktors $1/T= 10^6 \cdot \rm 1/s$: | |
| − | :$$ | + | :$${R}/{L} \hspace{0.25cm} = \hspace{0.2cm} 5 \cdot 10^{6 }\, {\rm 1/s} |
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}L= \frac{100\, {\rm \Omega}}{5 \cdot 10^6 \, {\rm | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}L= \frac{100\, {\rm \Omega}}{5 \cdot 10^6 \, {\rm | ||
| − | 1/s}}\hspace{0.15cm}\underline{= 20\,{\rm | + | 1/s}}\hspace{0.15cm}\underline{= 20\,{\rm µ H} \hspace{0.05cm}} ,$$ |
| − | + | :$${1}/({LC}) \hspace{0.25cm} = \hspace{0.2cm}4 \cdot 10^{12 }\, {\rm 1/s^2} | |
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}C= \frac{1}{4 \cdot 10^{12 }\, {\rm | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}C= \frac{1}{4 \cdot 10^{12 }\, {\rm | ||
1/s^2}\cdot 2 \cdot 10^{-5 }\, {\rm | 1/s^2}\cdot 2 \cdot 10^{-5 }\, {\rm | ||
| Zeile 86: | Zeile 96: | ||
} \hspace{0.15cm}\underline{= 12.5\,{\rm nF}} \hspace{0.05cm} .$$ | } \hspace{0.15cm}\underline{= 12.5\,{\rm nF}} \hspace{0.05cm} .$$ | ||
| − | + | ||
| + | |||
| + | '''(3)''' Die Sprungfunktion am Eingang wird durch $X_{\rm L}(p) = 1/p$ berücksichtigt. Damit ergibt sich | ||
:$$Y_{\rm L}(p)= \frac {p^2 +4} {p \cdot (p +1)\cdot(p +4 )} | :$$Y_{\rm L}(p)= \frac {p^2 +4} {p \cdot (p +1)\cdot(p +4 )} | ||
\hspace{0.05cm} ,$$ | \hspace{0.05cm} ,$$ | ||
| − | + | woraus man durch Anwendung des Residuensatzes die Zeitfunktion $y(t)$ ermitteln kann: | |
:$$y_1(t) \hspace{0.25cm} = \hspace{0.2cm} | :$$y_1(t) \hspace{0.25cm} = \hspace{0.2cm} | ||
\frac {p^2 +4} { (p +1)\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p | \frac {p^2 +4} { (p +1)\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p | ||
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}0}= 1 | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}0}= 1 | ||
| − | \hspace{0.05cm} , | + | \hspace{0.05cm} ,$$ |
| − | + | :$$ y_2(t) \hspace{0.25cm} = \hspace{0.2cm} | |
\frac {p^2 +4} { p\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p | \frac {p^2 +4} { p\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p | ||
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
| − | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= - | + | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= - {5}/{3}\cdot {\rm e}^{ |
\hspace{0.05cm}-t} | \hspace{0.05cm}-t} | ||
| − | \hspace{0.05cm} , | + | \hspace{0.05cm} ,$$ |
| − | + | :$$ y_3(t) \hspace{0.25cm} = \hspace{0.2cm} | |
\frac {p^2 +4} { p\cdot(p +1 )} \cdot {\rm e}^{\hspace{0.05cm}p | \frac {p^2 +4} { p\cdot(p +1 )} \cdot {\rm e}^{\hspace{0.05cm}p | ||
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
| − | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-4}= | + | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-4}= {5}/{3}\cdot {\rm e}^{ |
\hspace{0.05cm}-4t}$$ | \hspace{0.05cm}-4t}$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm}y(t)= y_1(t)+y_2(t)+y_3(t)= 1- | + | :$$\Rightarrow \hspace{0.3cm}y(t)= y_1(t)+y_2(t)+y_3(t)= 1- |
| − | {5}{3}\cdot {\rm e}^{ \hspace{0.05cm}-t/T}+\ | + | {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-t/T}+\ {5}/{3}\cdot {\rm |
e}^{ | e}^{ | ||
\hspace{0.05cm}-4t/T} | \hspace{0.05cm}-4t/T} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | :Hierbei ist berücksichtigt, dass die bei dieser Rechnung nicht berücksichtigte Konstante 10 | + | |
| + | [[Datei:P_ID1778__LZI_A_3_5_c.png|right|frame|Sprungantwort des RLC–Schwingkreises ]] | ||
| + | Hierbei ist berücksichtigt, dass die bei dieser Rechnung nicht berücksichtigte Konstante $10^6 \cdot \rm 1/s$ durch die Zeitnormierung auf $T = 1 \ \rm µ s$ ausgeglichen wird. | ||
| + | |||
| + | Die gesuchten Signalwerte lauten: | ||
| + | |||
:$$y(t = 0) \hspace{0.05cm}\underline{= 1.000}\hspace{0.05cm}, | :$$y(t = 0) \hspace{0.05cm}\underline{= 1.000}\hspace{0.05cm}, | ||
| − | \hspace{0.15cm}y(t = 0.5\,{\rm | + | \hspace{0.15cm}y(t = 0.5\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.215}\hspace{0.05cm}, $$ |
| − | + | :$$y(t = 2\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.775}\hspace{0.05cm}, | |
| − | \hspace{0.15cm}y(t = 5\,{\rm | + | \hspace{0.15cm}y(t = 5\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.989}\hspace{0.05cm}. $$ |
| − | |||
| − | |||
| − | |||
| − | + | Die Grafik zeigt den Signalverlauf. Die gesuchten Zahlenwerte sind nochmals eingetragen. | |
| − | :* Wegen | + | Man erkennt aus dieser Darstellung: |
| + | * Da extrem hohe Frequenzen durch das System (Bandsperre) nicht beeinflusst werden, ist auch im Ausgangssignal $y(t)$ der Sprung von $0$ auf $1$ mit unendlich großer Flankensteilheit zu erkennen. | ||
| + | * Wegen $H(f = 0) = 1$ ergibt der Grenzwert von $y(t)$ für $t → \infty$ folgerichtig ebenfalls den Wert $1$. | ||
| + | * Aufgrund der LC–Resonanzfrequenz bei $f_0 = 1/\pi$ (in $\rm MHz)$ kommt es zu einem Einbruch im Signalverlauf. | ||
| + | *Das Signalminimum von $\approx 0.215$ liegt bei etwa $t = 0.5 \ \rm µ s$. | ||
| − | |||
| − | : | + | [[Datei:P_ID1779__LZI_A_3_5_d.png|right|frame|Impulsantwort des RLC–Tiefpasses]] |
| + | '''(4)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | ||
| + | *Die Impulsantwort $h(t)$ ergibt sich aus der Sprungantwort $\sigma(t)=y(t)$ durch Differentiation: | ||
:$$h(t)= \frac{{\rm d}\hspace{0.1cm}y(t)}{{\rm | :$$h(t)= \frac{{\rm d}\hspace{0.1cm}y(t)}{{\rm | ||
d}t}= \delta (t) + \frac {5}{3T}\cdot {\rm e}^{ | d}t}= \delta (t) + \frac {5}{3T}\cdot {\rm e}^{ | ||
| Zeile 132: | Zeile 151: | ||
\hspace{0.05cm}-4t/T} | \hspace{0.05cm}-4t/T} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | *Der erste Lösungsvorschlag ist somit richtig, da die Differentiation einer Sprungfunktion die Diracfunktion liefert. | |
| − | :$$T \cdot h(t = 0 )\hspace{0.25cm} = \hspace{0.2cm} | + | *Für den kontinuierlichen Anteil von $h(t)$ erhält man folgende Zahlenwerte: |
| − | \hspace{0.05cm} , | + | :$$T \cdot h(t = 0 )\hspace{0.25cm} = \hspace{0.2cm} {5}/{3}- {20}/{3}= -5 |
| − | + | \hspace{0.05cm} ,$$ | |
| − | \hspace{0.05cm}-1}- | + | :$$ T \cdot h(t = T )\hspace{0.25cm} = \hspace{0.2cm} {5}/{3}\cdot {\rm e}^{ |
| − | \hspace{0.05cm}-4}= | + | \hspace{0.05cm}-1}- {20}/{3}\cdot {\rm e}^{ |
| + | \hspace{0.05cm}-4}= {5}/{3}\cdot 0.368- {20}/{3}\cdot | ||
0.018\approx 0.491 | 0.018\approx 0.491 | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | *Da $h(t)$ im Grenzfall für $t → \infty$ gegen Null strebt, ist der dritte Lösungsvorschlag ebenfalls richtig im Gegensatz zum zweiten. | |
| − | + | *Der Verlauf von $h(t)$ ist in der nebenstehenden Grafik dargestellt. | |
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 9. November 2021, 14:30 Uhr
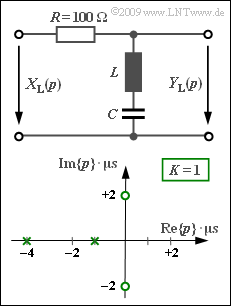
Wir betrachten einen Vierpol mit dem Widerstand $R = 100 \ \rm \Omega$ im Längszweig, während im Querzweig eine Induktivität $L$ und eine Kapazität $C$ in Serie geschaltet sind. Darunter gezeichnet ist das Pol–Nullstellen–Diagramm.
Beachten Sie die Normierung der komplexen Frequenz $p = {\rm j} \cdot 2 \pi f$ auf den Wert $1/T$ mit $T = 1 \ \rm µ s$. Dies hat zur Folge, dass zum Beispiel der Pol bei $-1$ in Realität bei $-10^6 \cdot \ \rm 1/s$ liegt.
Zur Berechnung von Zeitfunktionen kann man den Residuensatz anwenden:
- Bei $N$ einfachen Polen setzt sich der Ausgang $y(t)$ aus $N$ Eigenschwingungen ("Residuen") zusammen.
- Bei einem einfachen Pol bei $p_{{\rm x}i}$ gilt für das das Residuum:
- $${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \hspace{0.05cm} .$$
- Dieser Ansatz funktioniert aber nur dann, wenn die Anzahl $Z$ der Nullstellen kleiner ist als $N$, in dieser Aufgabe beispielsweise dann, wenn die Sprungantwort $\sigma(t)$ berechnet wird. In diesem Fall ist $Z = 2$ und $N = 3$, da zusätzlich die Sprungfunktion am Eingang durch $X_{\rm L}(p) = 1/p$ berücksichtigt werden muss.
- Für die Berechnung der Impulsantwort $h(t)$ funktioniert diese Vorgehensweise wegen $Z = N =2$ nicht.
- Hier kann man die Tatsache berücksichtigen, dass das Integral über die Impulsantwort $h(t)$ die Sprungantwort $\sigma(t)$ ergibt.
Hinweis:
- Die Aufgabe gehört zum Kapitel Laplace–Rücktransformation.
Fragebogen
Musterlösung
- Bei extrem tiefen Frequenzen $(f \rightarrow 0)$ hat die Kapazität $C$ einen unendlich großen Widerstand und bei sehr hohen Frequenzen $(f \rightarrow \infty)$ die Induktivität $L$.
- In beiden Fällen gilt $Y(f) = X(f)$ ⇒ $H(f) = 1$.
- Bei der Resonanzfrequenz $f_0$ wirkt dagegen die LC–Serienschaltung als Kurzschluss und es gilt $H(f = f_0) = 0$.
- Daraus folgt allein aus dem Blockschaltbild: Es handelt sich um eine Bandsperre.
(2) Aus dem Pol–Nullstellen–Diagramm ergibt sich die folgende $p$–Übertragungsfunktion $($ohne den Normierungsfaktor $1/T)$:
- $$H_{\rm L}(p)= \frac {(p - {\rm j} \cdot 2)(p + {\rm j} \cdot 2)} {(p +1)(p +4 )}= \frac {p^2 +4} {p^2 + 5 \cdot p +4} \hspace{0.05cm} .$$
- Unter Berücksichtigung der Spannungsteilereigenschaften erhält man mit dem Blindwiderstand $p \cdot L$ der Induktivität und dem Blindwiderstand $1/(p \cdot C)$ der Kapazität für die Schaltung:
- $$H_{\rm L}(p)= \frac { p\cdot L +1/(pC) } {R + p \cdot L +1/(pC) }= \frac { p^2 +1/(pC) } {p^2 + p \cdot {R}/{L} +1/(pC) }\hspace{0.05cm} .$$
- Durch Vergleich erkennt man unter Berücksichtigung des Normierungsfaktors $1/T= 10^6 \cdot \rm 1/s$:
- $${R}/{L} \hspace{0.25cm} = \hspace{0.2cm} 5 \cdot 10^{6 }\, {\rm 1/s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}L= \frac{100\, {\rm \Omega}}{5 \cdot 10^6 \, {\rm 1/s}}\hspace{0.15cm}\underline{= 20\,{\rm µ H} \hspace{0.05cm}} ,$$
- $${1}/({LC}) \hspace{0.25cm} = \hspace{0.2cm}4 \cdot 10^{12 }\, {\rm 1/s^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}C= \frac{1}{4 \cdot 10^{12 }\, {\rm 1/s^2}\cdot 2 \cdot 10^{-5 }\, {\rm \Omega \cdot s} } \hspace{0.15cm}\underline{= 12.5\,{\rm nF}} \hspace{0.05cm} .$$
(3) Die Sprungfunktion am Eingang wird durch $X_{\rm L}(p) = 1/p$ berücksichtigt. Damit ergibt sich
- $$Y_{\rm L}(p)= \frac {p^2 +4} {p \cdot (p +1)\cdot(p +4 )} \hspace{0.05cm} ,$$
woraus man durch Anwendung des Residuensatzes die Zeitfunktion $y(t)$ ermitteln kann:
- $$y_1(t) \hspace{0.25cm} = \hspace{0.2cm} \frac {p^2 +4} { (p +1)\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}0}= 1 \hspace{0.05cm} ,$$
- $$ y_2(t) \hspace{0.25cm} = \hspace{0.2cm} \frac {p^2 +4} { p\cdot(p +4 )} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= - {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-t} \hspace{0.05cm} ,$$
- $$ y_3(t) \hspace{0.25cm} = \hspace{0.2cm} \frac {p^2 +4} { p\cdot(p +1 )} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-4}= {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-4t}$$
- $$\Rightarrow \hspace{0.3cm}y(t)= y_1(t)+y_2(t)+y_3(t)= 1- {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-t/T}+\ {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-4t/T} \hspace{0.05cm} .$$
Hierbei ist berücksichtigt, dass die bei dieser Rechnung nicht berücksichtigte Konstante $10^6 \cdot \rm 1/s$ durch die Zeitnormierung auf $T = 1 \ \rm µ s$ ausgeglichen wird.
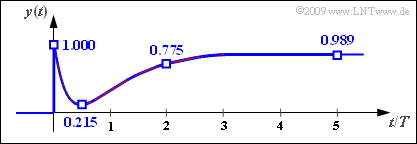
Die gesuchten Signalwerte lauten:
- $$y(t = 0) \hspace{0.05cm}\underline{= 1.000}\hspace{0.05cm}, \hspace{0.15cm}y(t = 0.5\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.215}\hspace{0.05cm}, $$
- $$y(t = 2\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.775}\hspace{0.05cm}, \hspace{0.15cm}y(t = 5\,{\rm µ s}) \hspace{0.05cm}\underline{= 0.989}\hspace{0.05cm}. $$
Die Grafik zeigt den Signalverlauf. Die gesuchten Zahlenwerte sind nochmals eingetragen.
Man erkennt aus dieser Darstellung:
- Da extrem hohe Frequenzen durch das System (Bandsperre) nicht beeinflusst werden, ist auch im Ausgangssignal $y(t)$ der Sprung von $0$ auf $1$ mit unendlich großer Flankensteilheit zu erkennen.
- Wegen $H(f = 0) = 1$ ergibt der Grenzwert von $y(t)$ für $t → \infty$ folgerichtig ebenfalls den Wert $1$.
- Aufgrund der LC–Resonanzfrequenz bei $f_0 = 1/\pi$ (in $\rm MHz)$ kommt es zu einem Einbruch im Signalverlauf.
- Das Signalminimum von $\approx 0.215$ liegt bei etwa $t = 0.5 \ \rm µ s$.
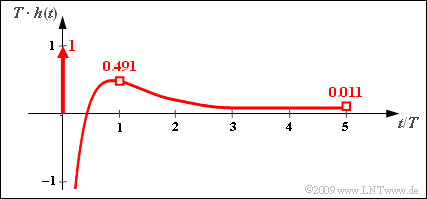
(4) Richtig sind die Lösungsvorschläge 1 und 3:
- Die Impulsantwort $h(t)$ ergibt sich aus der Sprungantwort $\sigma(t)=y(t)$ durch Differentiation:
- $$h(t)= \frac{{\rm d}\hspace{0.1cm}y(t)}{{\rm d}t}= \delta (t) + \frac {5}{3T}\cdot {\rm e}^{ \hspace{0.05cm}-t/T}- \frac {20}{3T}\cdot {\rm e}^{ \hspace{0.05cm}-4t/T} \hspace{0.05cm} .$$
- Der erste Lösungsvorschlag ist somit richtig, da die Differentiation einer Sprungfunktion die Diracfunktion liefert.
- Für den kontinuierlichen Anteil von $h(t)$ erhält man folgende Zahlenwerte:
- $$T \cdot h(t = 0 )\hspace{0.25cm} = \hspace{0.2cm} {5}/{3}- {20}/{3}= -5 \hspace{0.05cm} ,$$
- $$ T \cdot h(t = T )\hspace{0.25cm} = \hspace{0.2cm} {5}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-1}- {20}/{3}\cdot {\rm e}^{ \hspace{0.05cm}-4}= {5}/{3}\cdot 0.368- {20}/{3}\cdot 0.018\approx 0.491 \hspace{0.05cm} .$$
- Da $h(t)$ im Grenzfall für $t → \infty$ gegen Null strebt, ist der dritte Lösungsvorschlag ebenfalls richtig im Gegensatz zum zweiten.
- Der Verlauf von $h(t)$ ist in der nebenstehenden Grafik dargestellt.