Aufgaben:Aufgabe 3.5: Rekursive Filter für GF(2)

• Zurück zum Buch

Allgemeines rekursives Filter und betrachtete Realisierung

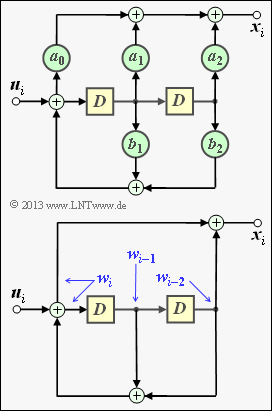
Die obere der beiden dargestellten Schaltungen zeigt ein rekursives Filter zweiter Ordnung in allgemeiner Form. Mit

$$A(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} a_0 + a_1 \cdot D + a_2 \cdot D^2 \hspace{0.05cm},$$

$$B(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 + b_1 \cdot D + b_2 \cdot D^2 $$

erhält man für die Übertragungsfunktion

$$G(D) = \frac{A(D)}{B(D)} = \frac{a_0 + a_1 \cdot D + a_2 \cdot D^2}{1 + b_1 \cdot D + b_2 \cdot D^2} \hspace{0.05cm}.$$

Zu beachten ist, dass sich alle Rechenoperationen auf ${\rm GF(2)}$ beziehen. Damit sind auch die Filterkoeffizienten $a_0, a_1, a_2, b_1$ und $b_2$ binär (entweder $0$ oder $1$).

Die untere Grafik zeigt das für die vorliegende Aufgabe spezifische Filter:

• Ein Filterkoeffizient ergibt sich zu $a_i = 1$, wenn die Verbindung durchgeschaltet ist $(0 ≤ i ≤ 2)$.
• Andernfalls ist $a_i = 0$. Die gleiche Systematik gilt für die Koeffizienten $b_1$ und $b_2$.

In den Teilaufgaben (1), ... , (3) sollen Sie für verschiedene Eingangssequenzen

• $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$,
• $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$,
• $\underline{u} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$

die jeweilige Ausgangssequenz $\underline{x}$ anhand der vorgegebenen Schaltung ermitteln. Es ist zu berücksichtigen:

• Besteht die Eingangssequenz $\underline{u}$ aus einer Eins gefolgt von lauter Nullen, so bezeichnet man diese spezifische Ausgangssequenz $\underline{x}$ als die Impulsantwort $\underline{g}$, und es gilt:

$$\underline{g} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm}{G}(D)\hspace{0.05cm}. $$

• Andernfalls ergibt sich die Ausgangssequenz als das Faltungsprodukt zwischen Eingangssequenz und Impulsantwort:

$$\underline{x} = \underline{u} * \underline{g} \hspace{0.05cm}.$$

• Die Faltungsoperation lässt sich mit dem Umweg über die $D$–Transformation umgehen.

Hinweise:

• Die Aufgabe gehört zum Kapitel Algebraische und polynomische Beschreibung.
• Bezug genommen wird insbesondere auf die Seite Filterstruktur bei gebrochen.–rationaler Übertragungsfunktion

Fragebogen

1

Welche Aussagen gelten für die Impulsantwort $\underline{g}$ des rekursiven Filters?

	Es gilt $\underline{g} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, ...)$.
	Es gilt $\underline{g} = (1, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, ...)$.
	Die Impulsantwort $\underline{g}$ ist unendlich weit ausgedehnt.

2

Es sei nun $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1)$. Welche Aussagen treffen zu?

	Die Ausgangssequenz lautet: $\underline{x} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, ...)$.
	Die Ausgangssequenz lautet: $\underline{x} = (1, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, ...)$.
	Die Ausgangssequenz $\underline{x}$ reicht bis ins Unendliche.

3

Nun gelte $\underline{u} = (1, \, 1, \, 1)$. Welche Aussagen treffen zu?

	Die Ausgangssequenz $\underline{x}$ beginnt mit $(1, \, 0, \, 1)$.
	Die Ausgangssequenz $\underline{x}$ beginnt mit $(1, \, 1, \, 1)$.
	Die Ausgangssequenz $\underline{x}$ reicht bis ins Unendliche.

4

Welche Aussagen gelten für die Übertragungsfunktion $G(D)$?

	Es gilt $G(D) = (1 + D^2)/(1 + D + D^2)$.
	Es gilt $G(D) = (1 + D + D^2)/(1 + D^2)$.
	Es gilt $G(D) = 1 + D + D^2 + D^4 + D^5 + D^7 + D^8 + \ ... \ $ .

Musterlösung

Musterlösung

(1)  Die Impulsantwort $\underline{g}$ ist gleich der Ausgangssequenz $\underline{x}$ für die Eingangssequenz $\underline{u} = (1, \, 0, \, 0, \, ...)$. Anhand der Filterstruktur ergibt sich mit $w_0 = w_{–1} = 0$ sowie den Gleichungen

Impulsantwort $\underline{g}$

$$w_i \hspace{-0.2cm} \ = \ \hspace{-0.2cm} u_i + w_{i-1} + w_{i-2} \hspace{0.05cm},$$

$$x_i \hspace{-0.2cm} \ = \ \hspace{-0.2cm} w_i + w_{i-2} $$

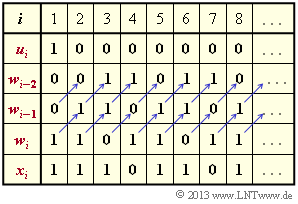
das Ergebnis $\underline{g} = \underline{x} = (1, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, ...)$ entsprechend Lösungsvorschlag 2, wie nebenstehende Berechnung zeigt.

Man erkennt aus diesem Berechnungsschema weiter folgende Periodizitäten der Impulsantwort $\underline{g}$ (bis ins Unendliche) wegen jeweils gleicher Registerbelegung:

$$g_3 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} g_6 = g_9 = \hspace{0.05cm}... \hspace{0.05cm}= 1 \hspace{0.05cm},$$

$$g_4 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} g_7 = g_{10} =\hspace{0.05cm} ... \hspace{0.05cm}= 0 \hspace{0.05cm},$$

$$g_5 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} g_8 = g_{11} =\hspace{0.05cm} ... \hspace{0.05cm}= 1 \hspace{0.05cm}.$$

Richtig ist also zusätzlich auch noch der Lösungsvorschlag 3.

(2) 

Berechnung der Ausgangssequenz $\underline{x}$

Nach ähnlichen Berechnungen wie in Teilaufgabe (1) erkennt man die Richtigkeit der Lösungsvorschläge 1 und 3. Auch die Ausgangssequenz $\underline{x}$ reicht bis ins Unendliche, und es zeigen sich wieder Periodizitäten.

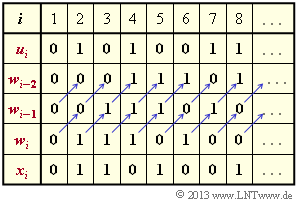
Zum gleichen Ergebnis gelangt man, wenn man die um eine, drei, sechs bzw. sieben Positionen (nach rechts) verschobenen Impulsantworten $\underline{g} = (1, \, 0, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, ...)$ im Galoisfeld ${\rm GF(2)}$ addiert:

$$\underline{x} \hspace{-0.2cm} \ = \ \hspace{-0.2cm} (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) + $$

$$\ + \ \hspace{-0.2cm} (0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) + $$

$$\ + \ \hspace{-0.2cm} (0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) + $$

$$\ + \ \hspace{-0.2cm} (0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) = $$

$$\ = \ \hspace{-0.2cm} (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) \hspace{0.05cm}. $$

Aufgrund der Linearität des betrachteten Systems ist dies erlaubt.

(3)  Hier wählen wir den Weg über die $D$–Transformierten:

$$\underline{u}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D + D^2 \hspace{0.05cm}.$$

Mit der Übertragungsfunktion $G(D) = (1 + D^2)/(1 + D + D^2)$ erhält man somit für die $D$–Transformierte der Ausgangssequenz:

$$X(D) = {U(D)} \cdot G(D) = {1+D+D^2} \cdot \frac{1+D^2}{1+D+D^2} = 1+D^2 \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm}\underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm} ) \hspace{0.05cm}.$$

Richtig ist demnach nur der Lösungsvorschlag 1: Trotz unendlich langer Impulsantwort $\underline{g}$ ist bei dieser Eingangssequenz $\underline{u}$ die Ausgangssequenz $\underline{x}$ auf drei Bit begrenzt. Zum gleichen Ergebnis kommt man wieder durch Addition verschobener Impulsantworten:

$$\underline{x} \hspace{-0.2cm} \ = \ \hspace{-0.2cm} (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) + $$

$$\ + \ \hspace{-0.2cm} (0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) + $$

$$\ + \ \hspace{-0.2cm} (0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) = $$

$$\ = \ \hspace{-0.2cm} (1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) \hspace{0.05cm}. $$

(4)  Auf dem Angabenblatt ist die allgemeine Übertragungsfunktion eines rekursiven Filters 2. Ordnung wie folgt gegeben.

$$G(D) = \frac{a_0 + a_1 \cdot D + a_2 \cdot D^2}{1 + b_1 \cdot D + b_2 \cdot D^2} \hspace{0.05cm}.$$

Das hier betrachtete Filter ist durch die Koeffizienten $a_0 = a_2 = b_1 = b_2 = 1$ und $a_1 = 0$ bestimmt. Somit erhält man das Ergebnis entsprechend dem Lösungsvorschlag 1:

$$G(D) = \frac{1 + D^2}{1 + D + D^2} \hspace{0.05cm}. $$

Gleichzeitig ist aber $G(D)$ auch die $D$–Transformierte der Impulsantwort:

$$\underline{g}= (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0 ,\hspace{0.05cm} ...\hspace{0.05cm}) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} {G}(D)= 1 + D + D^2 + D^4+ D^5 +... \hspace{0.1cm}. $$

$\rm GF(2)$–Polynomdivision

Das bedeutet: Richtig ist auch der Lösungsvorschlag 3.

Zum genau gleichen Ergebnis wäre man durch Division der beiden Polynome $1 + D^2$ und $1 + D + D^2$ gekommen, wie die Berechnung zeigt.