Aufgaben:Aufgabe 3.5: Rekursive Filter für GF(2): Unterschied zwischen den Versionen
| Zeile 25: | Zeile 25: | ||
:$$\underline{x} = \underline{u} * \underline{g} \hspace{0.05cm}.$$ | :$$\underline{x} = \underline{u} * \underline{g} \hspace{0.05cm}.$$ | ||
* Die Faltungsoperation lässt sich mit dem Umweg über die [[$D$–Transformation]] umgehen. | * Die Faltungsoperation lässt sich mit dem Umweg über die [[$D$–Transformation]] umgehen. | ||
| + | |||
''Hinweis:'' | ''Hinweis:'' | ||
Version vom 30. November 2017, 12:32 Uhr
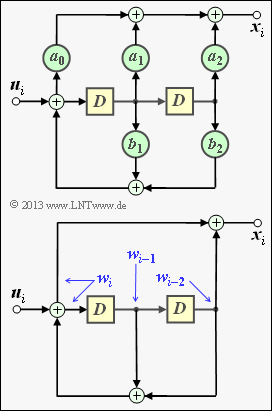
Die obere der beiden dargestellten Schaltungen zeigt ein rekursives Filter zweiter Ordnung in allgemeiner Form. Mit
- $$A(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} a_0 + a_1 \cdot D + a_2 \cdot D^2 \hspace{0.05cm},$$
- $$B(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 + b_1 \cdot D + b_2 \cdot D^2 $$
erhält man für die Übertragungsfunktion
- $$G(D) = \frac{A(D)}{B(D)} = \frac{a_0 + a_1 \cdot D + a_2 \cdot D^2}{1 + b_1 \cdot D + b_2 \cdot D^2} \hspace{0.05cm}.$$
Zu beachten ist, dass sich alle Rechenoperationen auf ${\rm GF(2)}$ beziehen. Damit sind auch die Filterkoeffizienten $a_0, a_1, a_2, b_1$ und $b_2$ binär (entweder $0$ oder $1$).
Die untere Grafik zeigt das für die vorliegende Aufgabe spezifische Filter. Ein Filterkoeffizient ergibt sich zu $a_i = 1$, wenn die Verbindung durchgeschaltet ist $(0 ≤ i ≤ 2)$. Andernfalls ist $a_i = 0$. Die gleiche Systematik gilt für die Koeffizienten $b_1$ und $b_2$.
In den Teilaufgaben (1), ... , (3) sollen Sie für verschiedene Eingangssequenzen
- $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, ...)$,
- $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, ...)$,
- $\underline{u} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, ...)$
die jeweilige Ausgangssequenz $\underline{x}$ anhand der vorgegebenen Schaltung ermitteln. Es ist zu berücksichtigen:
- Besteht die Eingangssequenz $\underline{u}$ aus einer Eins gefolgt von lauter Nullen, so bezeichnet man diese spezifische Ausgangssequenz $\underline{x}$ als die Impulsantwort $\underline{g}$, und es gilt:
- $$\underline{g} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm}{G}(D)\hspace{0.05cm}. $$
- Andernfalls ergibt sich die Ausgangssequenz als das Faltungsprodukt zwischen Eingangssequenz und Impulsantwort:
- $$\underline{x} = \underline{u} * \underline{g} \hspace{0.05cm}.$$
- Die Faltungsoperation lässt sich mit dem Umweg über die [[$D$–Transformation]] umgehen.
Hinweis:
- Die Aufgabe bezieht sich auf die Letzte Seite des Kapitels Algebraische und polynomische Beschreibung.
Fragebogen
Musterlösung