Aufgaben:Aufgabe 3.13: Vergleich SWE - DFE - ML

• Zurück zum Buch

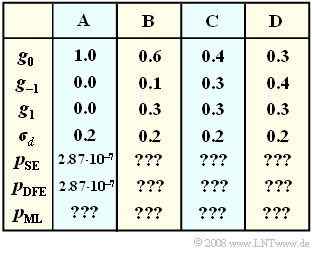
Fehlerwahrscheinlichkeiten im Vergleich:
SE:    Schwellenwertentscheidung,
DFE: Decision Feedback Equalization,
ML:    Maximum–Likelihood–Detektion

Es sollen Fehlerwahrscheinlichkeiten verschiedener Empfängertypen miteinander verglichen werden.  Betrachtet werden im Einzelnen:

• Schwellenwertentscheidung  $\rm (SE)$   ⇒   Fehlerwahrscheinlichkeit  $p_{\rm SE}$,
• Decision Feedback Equalization  $\rm (DFE)$   ⇒   Fehlerwahrscheinlichkeit  $p_{\rm DFE}$ und
• Maximum–Likelihood–Detektion  $\rm (ML)$   ⇒   Fehlerwahrscheinlichkeit  $p_{\rm ML}$.

In der Tabelle sind für vier verschiedene Parametersätze  $\rm A$,  $\rm B$,  $\rm C$  und  $\rm D$  angegeben:

• Der „Hauptwert”  $g_0$  des Detektionsgrundimpulses,
• der Vorläufer  $g_{\rm –1},$ 
• der Nachläufer  $g_1$  und
• der Detektionsstöreffektivwert  ($\sigma_d$)  vor dem jeweiligen Entscheider.

Ausgegangen wird von bipolaren Amplitudenkoeffizienten,  so dass zum Beispiel für die ungünstigste  (worst-case)  Fehlerwahrscheinlichkeit des Empfängers mit einfachem Schwellenwertenentscheider gilt:

$$p_{\rm U,\hspace{0.1cm} SE } = \left\{ \begin{array}{c} {\rm Q}\big [ ({g_0-|g_{-1}|-|g_{1}|})/{\sigma_d} \big ]\\ \\{\rm Q}(0) = 0.5 \end{array} \right.\quad \begin{array}{*{1}c} {\rm bei }\hspace{0.15cm}{\rm ge\ddot{o}ffnetem }\hspace{0.15cm}{\rm Auge }, \\ \\{\rm bei }\hspace{0.15cm}{\rm geschlossenem }\hspace{0.15cm}{\rm Auge }. \\ \end{array}\begin{array}{*{20}c} \\ \end{array}$$

Beim Nyquistsystem  $\rm A$  ist die mittlere Fehlerwahrscheinlichkeit genau so groß, nämlich

$$p_{\rm SE } =p_{\rm U,\hspace{0.1cm} SE } = {\rm Q}\left( {g_0}/{\sigma_d} \right)= {\rm Q}(5) \approx 2.87 \cdot 10^{-7}\hspace{0.05cm}.$$

Bei den anderen hier betrachteten Systemvarianten  $\rm B$,  $\rm C$  und  $\rm D$  sind die Impulsinterferenzen so stark und der vorgegebene Störeffektivwert so klein,  dass die folgende Näherung angewendet werden kann:

$$p_{\rm SE } \approx {1}/{4} \cdot p_{\rm U,\hspace{0.1cm} SE } = {1}/{4} \cdot {\rm Q}\left( \frac {{\rm Max }\hspace{0.05cm}\big [0, \hspace{0.05cm}g_0-|g_{-1}|-|g_{1}|\big ]}{\sigma_d} \right)\hspace{0.05cm}.$$

Mit Ausnahme des Nyquistsystems  $\rm A$  $($hier ist  $p_{\rm DFE} = p_{\rm SE})$  gilt für den DFE–Empfänger statt dessen folgende Näherung:

$$p_{\rm DFE } \approx {1}/{2} \cdot p_{\rm U,\hspace{0.1cm} DFE } = {1}/{2} \cdot {\rm Q}\left( \frac{{\rm Max }\hspace{0.05cm}\big [0, \hspace{0.05cm}g_0-|g_{-1}|\big ]}{\sigma_d} \right)\hspace{0.05cm}.$$

Dagegen wurde auf der  letzten Theorieseite  zu diesem Kapitel gezeigt, dass für einen Empfänger mit ML–Entscheidung die folgende Näherung zutrifft:

$$p_{\rm ML } = {\rm Q}\left( \frac{{\rm Max }\hspace{0.05cm}[g_{\nu}]}{\sigma_d} \right)\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  "Viterbi–Empfänger".

• Bezug genommen wird auch auf die Kapitel  "Lineare Nyquistentzerrung"  und  "Entscheidungsrückkopplung".

• Die Zahlenwerte der Q–Funktion können Sie mit dem Interaktionsmodul  "Komplementäre Gaußsche Fehlerfunktionen"  ermitteln.

• Um den im Theorieteil angegebenen Algorithmus für zwei Vorläufer anwenden zu können,  müssten Sie folgende Umbenennungen vornehmen  (was jedoch für die Berechnung der Fehlerwahrscheinlichkeiten keine Bedeutung hat):

$$g_{1 }\hspace{0.1cm}\Rightarrow \hspace{0.1cm}g_{0 },\hspace{0.4cm} g_{0 }\hspace{0.1cm}\Rightarrow \hspace{0.1cm}g_{-1 },\hspace{0.4cm} g_{-1 }\hspace{0.1cm}\Rightarrow \hspace{0.1cm}g_{-2 } \hspace{0.05cm}.$$

Fragebogen

1

Welche Fehlerwahrscheinlichkeit ergibt sich bei System  $\rm A$  mit Maximum–Likelihood–Detektion  $\rm (ML)$?

$\hspace{0.2cm} p_{\rm ML} \ = \ $ $\ \cdot 10^{\rm –7} $

2

Welche Fehlerwahrscheinlichkeiten sind bei System  $\rm B$  zu erwarten?

$\hspace{0.25cm} p_{\rm SE} \ = \ $ $\ \% $

$p_{\rm DFE} \ = \ $ $\ \% $

$\hspace{0.2cm} p_{\rm ML} \ = \ $ $\ \% $

3

Welche Fehlerwahrscheinlichkeiten ergeben sich bei System  $\rm C$?

$\hspace{0.25cm} p_{\rm SE} \ = \ $ $\ \% $

$p_{\rm DFE} \ = \ $ $\ \% $

$\hspace{0.2cm} p_{\rm ML} \ = \ $ $\ \% $

4

Welche Fehlerwahrscheinlichkeiten sind bei System  $\rm D$  zu erwarten?

$\hspace{0.25cm} p_{\rm SE} \ = \ $ $\ \% $

$p_{\rm DFE} \ = \ $ $\ \% $

$\hspace{0.2cm} p_{\rm ML} \ = \ $ $\ \% $

Musterlösung

Musterlösung

(1)  Ohne Impulsinterferenzen  $\text{(System A)}$  bringen der DFE– und der ML–Empfänger keine Verbesserung gegenüber der einfachen Schwellenwertentscheidung:

$$ p_{\rm DFE } = p_{\rm ML } = p_{\rm SE } \hspace{0.15cm}\underline {\approx 2.87 \cdot 10^{-7}} \hspace{0.05cm}.$$

(2)  Mit  $g_0 = 0.6$,  $g_{\rm –1} = 0.1$  und  $g_1 = 0.3$  $\text{(System B)}$ erhält man näherungsweise für die jeweiligen mittleren Fehlerwahrscheinlichkeiten:

$$p_{\rm SE } \ \approx \ {1}/{4} \cdot {\rm Q}\left( \frac{0.6-0.1-0.3}{0.2} \right)= {1}/{4} \cdot{\rm Q}(1) \hspace{0.15cm}\underline {\approx 4\% \hspace{0.05cm}},$$

$$ p_{\rm DFE } \ \approx \ {1}/{2} \cdot {\rm Q}\left( \frac{0.6-0.1}{0.2} \right)= {1}/{2} \cdot {\rm Q}(2.5) \hspace{0.15cm}\underline {\approx 0.31\%} \hspace{0.05cm},$$

$$ p_{\rm ML } \ \approx \ {\rm Q}\left( \frac{0.6}{0.2} \right) = {\rm Q}(3) \hspace{0.15cm}\underline {\approx 0.135\%} \hspace{0.05cm}.$$

(3)  Die mittleren Fehlerwahrscheinlichkeiten lauten mit  $g_0 = 0.4$  und  $g_1 = g_{\rm –1} = 0.3$  $\text{(System C)}$:

$$p_{\rm SE } \ \approx \ {1}/{4} \cdot{\rm Q}(0) \hspace{0.15cm}\underline {= 12.5\%} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm geschlossenes }\hspace{0.15cm}{\rm Auge } \hspace{0.05cm},$$

$$ p_{\rm DFE } \ \approx \ {1}/{2} \cdot {\rm Q}\left( \frac{0.4-0.3}{0.2} \right)= {1}/{2} \cdot {\rm Q}(0.5) \hspace{0.15cm}\underline {\approx 15\% \hspace{0.05cm}},$$

$$ p_{\rm ML } \ \approx \ {\rm Q}\left( \frac{0.4}{0.2} \right) = {\rm Q}(2) \hspace{0.15cm}\underline {\approx 2.27\%} \hspace{0.05cm}.$$

• Interessant ist – und nicht etwa ein Rechenfehler –, dass die DFE schlechter ist als der herkömmliche Schwellenwertentscheider,  wenn die Fehlerwahrscheinlichkeit $10\%$ oder mehr beträgt.
• Siehe dazu auch die Musterlösung zur Teilaufgabe  (4).

(4)  Bei System  $\text{D}$  ergibt sich auch für den DFE–Empfänger ein geschlossenes Auge.

• Die Fehlerwahrscheinlichkeit  $p_{\rm DFE}$  ist größer als  $p_{\rm SE}$,  da nun die ungünstigste Symbolfolge häufiger auftritt. Nach der angegebenen einfachen Näherung gilt:

$$p_{\rm SE } = {1}/{4} \cdot{\rm Q}(0) = 0.125\hspace{0.05cm}, \hspace{0.2cm} p_{\rm DFE } = {1}/{2} \cdot{\rm Q}(0) \hspace{0.15cm}\underline {= 0.250} \hspace{0.05cm}.$$

• Bei exakter Rechnung erhält man dagegen:

$$p_{\rm SE } \ = \ {1}/{4} \cdot {\rm Q}\left( \frac{0.3-0.4-0.3}{0.2}\right) + {1}/{4} \cdot{\rm Q}\left( \frac{0.3-0.4+0.3}{0.2}\right)+ \ {1}/{4} \cdot {\rm Q}\left( \frac{0.3+0.4-0.3}{0.2}\right) +{1}/{4} \cdot{\rm Q}\left( \frac{0.3+0.4+0.3}{0.2}\right)$$

$$ \Rightarrow \hspace{0.3cm}p_{\rm SE } \ = \ {1}/{4} \cdot \left[ {\rm Q}(-2) + {\rm Q}(1) +{\rm Q}(2) +{\rm Q}(5) \right] ={1}/{4} \cdot \left[ 1+ {\rm Q}(1) +{\rm Q}(5) \right] \hspace{0.05cm}.$$

• Wegen  ${\rm Q}(–2) + {\rm Q}(2) = 1$  und  ${\rm Q}(5) \approx 0$  erhält man daraus  $p_{\rm SE} \approx 25.5\%$.

• Entsprechend gilt für den DFE–Empfänger:

$$p_{\rm DFE } \ = \ {1}/{2} \cdot {\rm Q}\left( \frac{0.3-0.4}{0.2}\right) + {1}/{2} \cdot{\rm Q}\left( \frac{0.3+0.4}{0.2}\right)= \ {1}/{2} \cdot \left[ {\rm Q}(-0.5) + {\rm Q}(3.5) \right] \approx\frac{1- {\rm Q}(0.5)}{2}\hspace{0.15cm}\underline {= 35\%} \hspace{0.05cm}.$$

• Dagegen beträgt die Fehlerwahrscheinlichkeit  $p_{\rm ML}$  eines Maximum–Likelihood–Empfängers weiterhin ${\rm Q}(2) \hspace{0.15cm} \underline {= 2.27\%}$.

• Die Reihenfolge der Detektionsgrundimpulswerte ist für die Fehlerwahrscheinlichkeit des Viterbi–Empfängers  (nahezu)  nicht von Bedeutung.