Aufgaben:Aufgabe 3.12: Trellisdiagramm für zwei Vorläufer: Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
Zur Berechnung der minimalen Gesamtfehlergröße ${\it \Gamma}_2(10)$ in den Teilaufgaben (1) und (2) soll von folgenden Zahlenwerten ausgegangen werden: | Zur Berechnung der minimalen Gesamtfehlergröße ${\it \Gamma}_2(10)$ in den Teilaufgaben (1) und (2) soll von folgenden Zahlenwerten ausgegangen werden: | ||
| + | * unipolare Amplitudenkoeffizienten: $a_{\rm \nu} ∈ \{0, 1\}$, | ||
| + | * Grundimpulswerte $g_0 = 0.5$, $g_{\rm –1} = 0.3$, $g_{\rm –2} = 0.2}$, | ||
| + | * anliegender Detektionsabtastwert: $d_2 = 0.2$, | ||
| + | * Minimale Gesamtfehlergrößen zum Zeitpunkt $\nu = 1$: | ||
| + | :$${\it \Gamma}_{1}(00) = 0.0,\hspace{0.2cm}{\it \Gamma}_{1}(01) = 0.2, \hspace{1cm} {\it \Gamma}_{1}(10) = 0.6,\hspace{0.2cm}{\it \Gamma}_{1}(11) = | ||
| + | 1.2 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
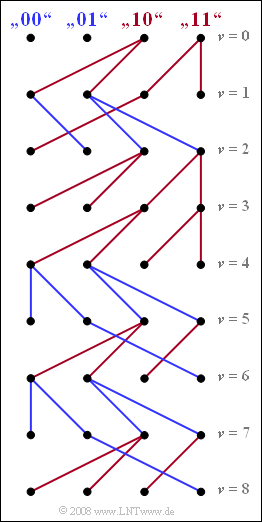
| + | In der Grafik ist das vereinfachte Trellisdiagramm für die Zeitpunkte $\nu = 1$ bis $\nu = 8$ dargestellt. Blaue Zweige kommen entweder von ${\it \Gamma}_{\rm \nu –1}(00)$ oder von ${\it \Gamma}_{\rm \nu –1}(01)$ und kennzeichnen eine hypothetische „$0$”. Dagegen weisen alle roten Zweige – ausgehend von den Zuständen ${\it \Gamma}_{\rm \nu –1}(10)$ bzw. ${\it \Gamma}_{\rm \nu –1}(11)$ – jeweils auf das Symbol „$1$” hin | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Themengebiet von Kapitel [[Digitalsignal%C3%BCbertragung/Viterbi%E2%80%93Empf%C3%A4nger| Viterbi–Empfänger]]. | ||
| + | * Alle Größen sind hier normiert zu verstehen. | ||
| + | * Die hier angesprochene Thematik wird auch im folgenden Interaktionsmodul behandelt: [https://intern.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=2010&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross| Eigenschaften des Viterbi–Empfängers]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
{Multiple-Choice Frage | {Multiple-Choice Frage | ||
Version vom 3. November 2017, 11:34 Uhr
Wir gehen von den Grundimpulswerten $g_0$, $g_{\rm –1}$ und $g_{\rm &ndash2}$ aus. Das bedeutet, dass die Entscheidung über das Symbol $a_{\rm \nu}$ auch durch die nachfolgenden Koeffizienten $a_{\rm \nu +1}$ und $a_{\rm \nu +2}$ beeinflusst wird. Damit sind für jeden Zeitpunkt $\nu$ genau $8$ Fehlergrößen $\epsilon_{\rm \nu}$ zu berechnen, aus denen die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(00)$, ${\it \Gamma}_{\rm \nu}(01)$, ${\it \Gamma}_{\rm \nu}(10)$ und ${\it \Gamma}_{\rm \nu}(11)$ berechnet werden können. Hierbei liefert beispielsweise ${\it \Gamma}_{\rm \nu}(01)$ Information über das Symbol $a_{\rm \nu}$ unter der Annahme, dass $a_{\rm \nu +1} = 0$ und $a_{\rm \nu +2} = 1$ sein werden. Die minimale Gesamtfehlergröße ${\it \Gamma}_{\rm \nu}(01)$ ist hierbei der kleinere Wert aus dem Vergleich von
- $${\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001) \hspace{0.15cm}{\rm und} \hspace{0.15cm}{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101).$$
Zur Berechnung der minimalen Gesamtfehlergröße ${\it \Gamma}_2(10)$ in den Teilaufgaben (1) und (2) soll von folgenden Zahlenwerten ausgegangen werden:
- unipolare Amplitudenkoeffizienten: $a_{\rm \nu} ∈ \{0, 1\}$,
- Grundimpulswerte $g_0 = 0.5$, $g_{\rm –1} = 0.3$, $g_{\rm –2} = 0.2}$,
- anliegender Detektionsabtastwert: $d_2 = 0.2$,
- Minimale Gesamtfehlergrößen zum Zeitpunkt $\nu = 1$:
- $${\it \Gamma}_{1}(00) = 0.0,\hspace{0.2cm}{\it \Gamma}_{1}(01) = 0.2, \hspace{1cm} {\it \Gamma}_{1}(10) = 0.6,\hspace{0.2cm}{\it \Gamma}_{1}(11) = 1.2 \hspace{0.05cm}.$$
In der Grafik ist das vereinfachte Trellisdiagramm für die Zeitpunkte $\nu = 1$ bis $\nu = 8$ dargestellt. Blaue Zweige kommen entweder von ${\it \Gamma}_{\rm \nu –1}(00)$ oder von ${\it \Gamma}_{\rm \nu –1}(01)$ und kennzeichnen eine hypothetische „$0$”. Dagegen weisen alle roten Zweige – ausgehend von den Zuständen ${\it \Gamma}_{\rm \nu –1}(10)$ bzw. ${\it \Gamma}_{\rm \nu –1}(11)$ – jeweils auf das Symbol „$1$” hin
Hinweise:
- Die Aufgabe gehört zum Themengebiet von Kapitel Viterbi–Empfänger.
- Alle Größen sind hier normiert zu verstehen.
- Die hier angesprochene Thematik wird auch im folgenden Interaktionsmodul behandelt: Eigenschaften des Viterbi–Empfängers.
Fragebogen
Musterlösung