Aufgabe 3.12: Pfadgewichtsfunktion

• Zurück zum Buch

Faltungscodierer mit $m = 1$ und zugehöriges Zustandsübergangsdiagramm

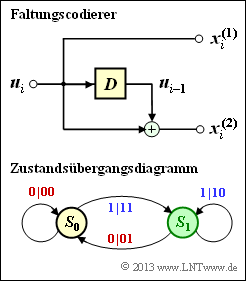
In Aufgabe A3.6 wurde das Zustandsübergangsdiagramm für den gezeichneten Faltungscoder mit den Eigenschaften

• Rate $R = 1/2$,
• Gedächtnis $m = 1$,
• Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1, \, D)$

ermittelt, das ebenfalls rechts dargestellt ist.

Es soll nun aus dem Zustandsübergangsdiagramm

• die Pfadgewichtsfunktion $T(X)$, und
• die erweiterte Pfadgewichtsfunktion $T_{\rm enh}(X, \, U)$

bestimmt werden, wobei $X$ und $U$ Dummy–Variablen sind.

Die Vorgehensweise ist im Theorieteil zu diesem Kapitel eingehend erläutert. Schließlich ist aus $T(X)$ noch die freie Distanz $d_{\rm F}$ zu bestimmen.

Hinweise:

• Die Aufgabe gehört zum Themengebiet des Kapitels Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken
• Berücksichtigen Sie bei der Lösung die Reihenentwicklung

$$\frac{1}{1-x} = 1 + x + x^2 + x^3 + \hspace{0.05cm}...\hspace{0.1cm}.$$

• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Was ist bei der Modifizierung des Übergangsdiagramms zu beachten?

	Der Zustand $S_0$ muss in $S_0$ und $S_0'$ aufgespalten werden.
	Der Zustand $S_1$ muss in $S_1$ und $S_1'$ aufgespalten werden.
	Der Übergang von $S_0$ nach $S_1$ ist mit $UX^2$ zu beschriften.
	Der Übergang von $S_1$ nach $S_1$ ist mit $UX$ zu beschriften.
	Der Übergang von $S_1$ nach $S_0'$ ist mit $X$ zu beschriften.

2

Welche Gleichungen gelten für die erweiterte Pfadgewichtsfunktion?

	$T_{\rm enh}(X, \, U) = U^2X^3$
	$T_{\rm enh}(X, \, U) = UX^3/(1 \, –UX)$
	$T_{\rm enh}(X, \, U) = UX^3 + U^2X^4 + U^3X^5 + \, ...$

3

Welche Gleichungen gelten für die „einfache” Pfadgewichtsfunktion?

	$T(X) = X^3/(1 \, –X)$,
	$T(X) = X^3 + X^4 + X^5 + \, ... $

4

Wie groß ist die freie Distanz des betrachteten Codes?

$d_{\rm F} \ = \ $

Musterlösung

Musterlösung

(1) 

Modifiziertes Zustandsübergangsdiagramm

Der Zustand $S_0$ muss entsprechend nebenstehender Grafik in einen Startzustand $S_0$ und einen Endzustand $S_0'$ aufgespalten werden. Der Grund hierfür ist, dass für die folgende Berechnung der Pfadgewichtsfunktion $T(X, \, U)$ alle Übergänge von $S_0$ nach nach $S_0$ ausgeschlossen werden müssen.

Jedes Codesymbol $x ∈ \{0, \, 1\}$ wird durch $X^x$ dargestellt, wobei $X$ eine Dummy–Variable hinsichtlich der Ausgangssequenz ist: $x = 0 \ \Rightarrow \ X^0 = 1, \ x = 1 \ \Rightarrow \ X^1 = X.$ Daraus folgt weiter $(00) \ \Rightarrow \ 1, \ (01) \ \Rightarrow \ X, \ (10) \ \Rightarrow \ X, \ (11) \ \Rightarrow \ X^2$.

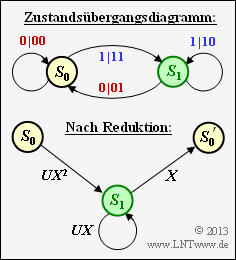
Bei einem blauen Übergang im ursprünglichen Diagramm – dies steht für $u_i = 1$ – ist im modifizierten Diagramm der Faktor $U$ hinzuzufügen. Aus der nebenstehenden Grafik erkennt man, dass die Lösungsvorschläge 1, 3, 4 und 5 richtig sind.

(2)  Das reduzierte Diagramm ist entsprechend der Auflistung im Theorieteil ein „Ring”. Daraus folgt:

$$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} \hspace{0.05cm}.$$

Mit $A(X, \, U) = UX^2, \ B(X, \, U) = X, \ C(X, \, U) = UX$ erhält man mit der angegebenen Reihenentwicklung:

$$T_{\rm enh}(X, U) = \frac{U \hspace{0.05cm} X^3}{1- U \hspace{0.05cm} X} = U \hspace{0.05cm} X^3 \cdot \left [ 1 + (U \hspace{0.05cm} X) + (U \hspace{0.05cm} X)^2 + ... \hspace{0.10cm} \right ] \hspace{0.05cm}.$$

Richtig sind somit die Lösungsvorschläge 2 und 3.

(3)  Man kommt von der erweiterten Pfadgewichtsfunktion zu $T(X)$, indem der Formalparameter $U = 1$ gesetzt wird. Richtig sind also beide Lösungsvorschläge.

(4)  Die freie Distanz $d_{\rm F}$ lässt sich aus der Pfadgewichtsfunktion $T(X)$ ablesen, und zwar als der niedrigste Exponent der Dummy–Variablen $X \ \Rightarrow \ d_{\rm F} \ \underline{= 3}$.