Aufgaben:Aufgabe 3.11: Tschebyscheffsche Ungleichung: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID139__Sto_A_3_11.png|right|Beispielhafte Tschebyscheffsch–Schranke] | + | [[Datei:P_ID139__Sto_A_3_11.png|right|Beispielhafte Tschebyscheffsch–Schranke]] |
Ist über eine Zufallsgröße $x$ nichts weiter bekannt als nur | Ist über eine Zufallsgröße $x$ nichts weiter bekannt als nur | ||
*der Mittelwert $m_x$ und | *der Mittelwert $m_x$ und | ||
| Zeile 15: | Zeile 15: | ||
*Der grüne Kurvenverlauf zeigt die tatsächliche Wahrscheinlichkeit bei der Gleichverteilung. | *Der grüne Kurvenverlauf zeigt die tatsächliche Wahrscheinlichkeit bei der Gleichverteilung. | ||
*Die blauen Punkte gelten für die Exponentialverteilung. | *Die blauen Punkte gelten für die Exponentialverteilung. | ||
| + | |||
Aus dieser Darstellung ist zu erkennen, dass die <i>Tschebyscheffsche Ungleichung</i> nur eine sehr grobe Schranke darstellt. Sie sollte nur dann verwendet werden, wenn von der Zufallsgröße wirklich nur der Mittelwert und die Streuung bekannt sind. | Aus dieser Darstellung ist zu erkennen, dass die <i>Tschebyscheffsche Ungleichung</i> nur eine sehr grobe Schranke darstellt. Sie sollte nur dann verwendet werden, wenn von der Zufallsgröße wirklich nur der Mittelwert und die Streuung bekannt sind. | ||
| Zeile 30: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche der | + | {Welche der folgenden Aussagen sind zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | - Vorstellbar ist eine Zufallsgröße mit Pr(| | + | - Vorstellbar ist eine Zufallsgröße mit ${\rm Pr}(|x -m_x> | \ge 3\sigma_x) = 1/4$. |
| − | + „Tschebyscheff” liefert für < | + | + „Tschebyscheff” liefert für $\varepsilon < \sigma_x$ keine Information. |
| − | + Pr(| | + | + ${\rm Pr}(|x -m_x> | \ge \sigma_x)$ist für große $\varepsilon$ identisch $0$, wenn $x$ begrenzt ist. |
| − | {Geben Sie die Überschreitungswahrscheinlichkeit | + | {Es gelte $k = 1, 2, 3, 4$. Geben Sie die Überschreitungswahrscheinlichkeit $p_k = {\rm Pr}(|x -m_x | \ge k \cdot \sigma_x)$ für die Gaußverteilung an. <br>Wie groß ist $p_3$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(|x - m_x| | + | $\text{Gauß}$: ${\rm Pr}(|x -m_x | \ge 3 \sigma_x) \ = $ { 0.26 3% } $\ \%$ |
| − | { | + | {Welche Überschreitungswahrscheinlichkeiten $p_k$ ergeben sich bei der Exponentialverteilung. Hier gilt $m_x = \sigma_x = 1/\lambda$. <br>Wie groß ist $p_3$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(|x - m_x| | + | $\text{Exponential}$: ${\rm Pr}(|x -m_x | \ge 3 \sigma_x) \ = $ { 1.83 3% } $\ \%$ |
Version vom 15. März 2017, 17:34 Uhr
Ist über eine Zufallsgröße $x$ nichts weiter bekannt als nur
- der Mittelwert $m_x$ und
- die Streuung $\sigma_x$,
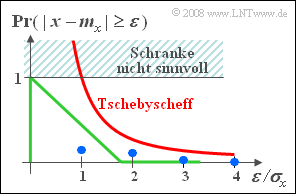
so gibt die Tschebyscheffsche Ungleichung eine obere Schranke für die Wahrscheinlichkeit an, dass $x$ betragsmäßig mehr als einen Wert $\varepsilon$ von seinem Mittelwert $m_x$ abweicht. Diese Schranke lautet: $${\rm Pr}(|x-m_x|\ge \varepsilon) \le {\sigma_x^{\rm 2}}/{\varepsilon^{\rm 2}}.$$
Zur Erläuterung:
- In der Grafik ist diese obere Schranke rot eingezeichnet.
- Der grüne Kurvenverlauf zeigt die tatsächliche Wahrscheinlichkeit bei der Gleichverteilung.
- Die blauen Punkte gelten für die Exponentialverteilung.
Aus dieser Darstellung ist zu erkennen, dass die Tschebyscheffsche Ungleichung nur eine sehr grobe Schranke darstellt. Sie sollte nur dann verwendet werden, wenn von der Zufallsgröße wirklich nur der Mittelwert und die Streuung bekannt sind.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Verteilungen.
- Insbesondere wird auf die Seiten Tschebyscheffsche Ungleichung Bezug genommen .
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
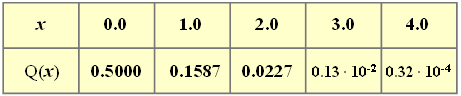
- Nachfolgend finden Sie eine Tabelle mit Werten der komplementären Gaußschen Fehlerfunktion.
Fragebogen
Musterlösung
- 1. Die erste Aussage ist falsch. Die Tschebyscheffsche Ungleichung liefert hier die Schranke 1/9. Bei keiner Verteilung kann die hier betrachtete Wahrscheinlichkeit größer sein.
- Für ε < σx liefert Tschebyscheff einen Wert größer als 1. Da eine Wahrscheinlichkeit nie größer als 1 sein kann, ist diese Information nutzlos.
- Auch die letzte Aussage ist zutreffend. Beispielsweise gilt bei der Gleichverteilung:
- $$\rm Pr(|\it x- m_x | \ge \varepsilon)=\left\{ \begin{array}{*{4}{c}} 1-{\varepsilon}/{\varepsilon_{\rm 0}} & \rm f\ddot{u}r\hspace{0.1cm}{\it \varepsilon<\varepsilon_{\rm 0}=\sqrt{\rm 3}\cdot\sigma_x},\\\rm 0 & \rm sonst. \end{array} \right. $$
- Richtig sind demnach die Lösungsvorschläge 2 und 3
- 2. Bei der Gaußverteilung gilt:
- $$p_k=\rm Pr(|\it x-m_x| \ge k\cdot\sigma_{x})=\rm 2\cdot \rm Q(\it k).$$
- Daraus ergeben sich folgende Zahlenwerte (in Klammern: Schranke nach Tschebyscheff):
- $$k=\rm 1: \rm Pr(|\it x-m_x| \ge \sigma_{x}) = \rm 0.317 \hspace{0.3cm}(1.000),$$
- $$k=\rm 2: \rm Pr(|\it x-\it m_x| \ge \rm 2\it \cdot\sigma_{x}) = \rm 0.454\cdot 10^{-1} \hspace{0.3cm}(0.250),$$
- $$k=\rm 3: \rm Pr(|\it x- \it m_x| \ge \rm 3\cdot\it \sigma_{x}) \hspace{0.15cm}\underline{ = \rm 0.26\cdot 10^{-2}} \hspace{0.45cm}\rm (0.111),$$
- $$k=\rm 4: \rm Pr(|\it x- \it m_x| \ge \rm 4\cdot\it \sigma_{x}) = \rm 0.64\cdot 10^{-4} \hspace{0.3cm}(0.0625).$$
- 3. Ohne Einschränkung der Allgemeingültigkeit setzen wir λ = 1
- ⇒ mx = σx = 1. Dann gilt:
- $$\rm Pr(|\it x - \it m_x| \ge \it k\cdot\sigma_{x}) = \rm Pr(|\it x-\rm 1| \ge \it k).$$
- Da in diesem Sonderfall die Zufallsgröße x stets größer als 0 ist, gilt weiter:
- $$\it p_k= \rm Pr(\it x \ge k+\rm 1)=\int_{\it k+\rm 1}^{\infty}\hspace{-0.15cm} \rm e^{-\it x}\, {\rm d}\it x=\rm \rm e^{-(\it k + \rm 1)}.$$
- Daraus ergeben sich folgende Zahlenwerte für die Exponentialverteilung:
- $$k=\rm 1: \rm Pr(|\it x-m_x| \ge \sigma_{x}) = \rm \rm e^{-2}= \rm 0.1353,$$
- $$k=\rm 2: \rm Pr(|\it x- \it m_x| \ge \rm 2\it \cdot\sigma_{x}) = \rm \rm e^{-3}=\rm 0.0497 ,$$
- $$k=\rm 3: \rm Pr(|\it x-\it m_x| \ge \rm 3\cdot\it \sigma_{x}) = \rm \rm e^{-4}\hspace{0.15cm}\underline{ =\rm 0.0183 },$$
- $$k=\rm 4: \rm Pr(|\it x- \it m_x| \ge \rm 4\cdot\it \sigma_{x}) = \rm \rm e^{-5}= \rm 0.0067.$$