Aufgabe 3.09Z: Nochmals Viterbi–Algorithmus

• Zurück zum Buch

Trellis für einen Rate–1/2–Code mit Gedächtnis $m = 1$

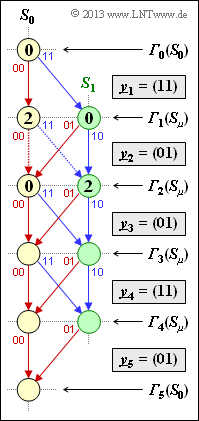
Die Grafik zeigt das Trellisdiagramm das Faltungscodes entsprechend Aufgabe A3.6, gekennzeichnet durch folgende Größen:

• Rate 1/2  ⇒  $k = 1, \ n = 2$,
• Gedächtnis $m = 1$,
• Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1, \ 1 + D)$,
• Länge der Informationssequenz: $L = 4$,
• Sequenzlänge inklusive Terminierung: $L' = L + m = 5$.

Anhand dieser Darstellung soll die Viterbi–Decodierung schrittweise nachvollzogen werde, wobei von der folgenden Empfangssequenz auszugehen ist: $\underline{y} = (11, \, 01, \, 01, \, 11, \, 01)$.

In das Trellis eingezeichnet sind:

• Der Initialwert ${\it \Gamma}_0(S_0)$ für den Viterbi–Algorithmus wird stets zu $0$ gewählt.
• Die beiden Fehlergrößen für den ersten Decodierschritt $(i = 1)$ erhält man mit $\underline{y}_1 = (11)$ wie folgt:

$${\it \Gamma}_1(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 2 \hspace{0.05cm},$$

$${\it \Gamma}_1(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 0 \hspace{0.05cm}.$$

• Die Fehlergrößen zum Schritt $i = 2$  ⇒  $\underline{y}_2 = (01)$ ergeben sich durch folgende Vergleiche:

$${\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] =$$

$$\ = \ \hspace{-0.15cm} {\rm min} \left [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+0 \right ] = 0\hspace{0.05cm},$$

$${\it \Gamma}_2(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] =$$

$$\ = \ \hspace{-0.15cm} {\rm min} \left [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+2 \right ] = 2\hspace{0.05cm}.$$

In gleicher Weise sollen Sie

• die Fehlergrößen zu den Zeitpunkten $i = 3, \ i = 4$ und $i = 5$ (Terminierung) berechnen, und
• die jeweils ungünstigeren Wege zu einem Knoten ${\it \Gamma}_i(S_{\mu})$ eliminieren. In der Grafik ist dies für $i = 2$ durch punktierte Linien angedeutet.

Anschließend ist der durchgehende Pfad von ${\it \Gamma}_0(S_0)$ bis ${\it \Gamma}_5(S_0)$ zu finden, wobei die Rückwärtsrichtung zu empfehlen ist. Verfolgt man den gefundenen Pfad in Vorwärtsrichtung, so erkennt man

• die wahrscheinlichste Codesequenz $\underline{z}$ (im Idealfall gleich $\underline{x}$) an den Beschriftungen,
• die wahscheinlichste Informationssequenz $\underline{\upsilon}$ (im Idealfall gleich $\underline{u}$) an den Farben.

Hinweis:

• Die Aufgabe gehört zum Kapitel Kapitel 3.4.

Fragebogen

1

Berechnen Sie die minimalen Fehlergrößen für den Zeitpunkt $i = 3$.

${\it \Gamma}_3(S_0) \ = \ $

${\it \Gamma}_3(S_1) \ = \ $

2

Berechnen Sie die minimalen Fehlergrößen für den Zeitpunkt $i = 4$.

${\it \Gamma}_4(S_0) \ = \ $

${\it \Gamma}_4(S_1) \ = \ $

3

Berechnen Sie die minimale Fehlergröße für den Zeitpunkt $i = 5$ (Ende).

${\it \Gamma}_5(S_0) \ = \ $

4

Welche endgültigen Ergebnisse liefert der Viterbi–Algorithmus:

	$\underline{z} = (11, \, 01, \, 00, \, 11, \, 01)$.
	$\underline{z} = (11, \, 01, \, 11, \, 01, \, 00)$.
	$\underline{\upsilon} = (1, \, 0, \, 0, \, 1, \, 0)$.
	$\underline{\upsilon} = (1, \, 0, \, 1, \, 0, \, 0)$.

5

Welche Entscheidung wäre ohne Terminierung getroffen worden?

	Die gleiche,
	eine andere.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)