Aufgabe 3.09: Korrelationsempfänger für unipolare Signalisierung

Beispielhafte Korrelationswerte

Betrachtet wird die gemeinsame Entscheidung von $N = 3$ Binärsymbolen (Bit) mittels des Korrelationsempfängers. Die $M = 8$ möglichen Quellensymbolfolgen $Q_i$ besitzen alle die gleiche Wahrscheinlichkeit und sie sind durch die folgenden unipolaren Amplitudenkoeffizienten festgelegt:

$$Q_0 = 000, \hspace{0.15cm}Q_1 = 001,\hspace{0.15cm}Q_2 = 010,\hspace{0.15cm}Q_3 = 011 \hspace{0.05cm},$$

$$Q_4 = 100, \hspace{0.15cm}Q_5 = 101,\hspace{0.15cm}Q_6 = 110,\hspace{0.15cm}Q_7 = 111 \hspace{0.05cm}.$$

Die möglichen Sendesignale $s_i(t)$ – jeweils mit der Dauer $3T$ – sind alle rechteckförmig mit Ausnahme von $s_0(t) = 0$. Die Signale $s_1(t)$, $s_2(t)$, und $s_4(t)$ mit nur jeweils einer „$1$” besitzen die Signalenergie $E_{\rm B}$ (steht für „Energie pro Bit”), während zum Beispiel die Energie von $s_7(t)$ gleich $3E_{\rm B}$ beträgt.

Der Korrelationsempfänger bildet aus dem verrauschten Empfangssignal $r(t) = s(t) + n(t)$ insgesamt $2^3 = 8$ Entscheidungsgrößen (Metriken)

$$W_i = I_i - {E_i}/{2 }\hspace{0.3cm}{\rm mit}\hspace{0.3cm} I_i =\int_{0}^{3T} r(t) \cdot s_i(t) \,{\rm d} t \hspace{0.3cm}( i = 0, ... , 7)$$

und setzt die Sinkensymbolfolge $V = Q_j$, falls $W_j$ größer ist als alle anderen $W_{\it i≠j}$. Damit trifft er eine optimale Entscheidung im Sinne von Maximum–Likelihood.

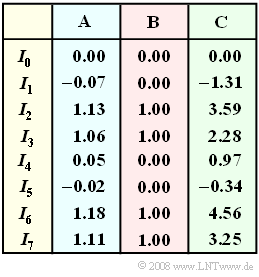
In der Tabelle sind die (unkorrigierten) Korrelationswerte $I_0, \ ... \ , I_7$ für drei verschiedene Systeme angegeben, die sich hinsichtlich der Störungen $n(t)$ unterscheiden und mit A, B oder C bezeichnet werden. Eine dieser Spalten steht für „keine Störung”, eine für „geringe Störungen” und eine weitere für „starke Störungen”. Zur Bestimmung der Metriken für die drei Systemvarianten wurde stets die gleiche Quellensymbolfolge gesendet.

Hinweis:

Die Aufgabe gehört zum Themengebiet von Kapitel Optimale Empfängerstrategien dieses Buches.

Fragebogen

	System A,
	System B,
	System C.

$k$ =

${\rm System \ A} \text{:} \hspace{0.2cm} j$ =

${\rm System \ C} \text{:} \hspace{0.2cm} j$ =

	System A,
	System B,
	System C.

	Die Differenz zwischen $W_2$ und dem nächstgrößten Wert $W_{\it i ≠ 2}$ ist um so kleiner, je stärker die Störungen sind.
	Wenn es zu einer Verfälschung kommt, dann entscheidet sich der Empfänger am wahrscheinlichsten für die Symbolfolge $Q_6$.
	Die Wahrscheinlichkeiten für fehlerhafte Entscheidungen zugunsten von $Q_0$, $Q_3$ bzw. $Q_6$ sind gleich.

Musterlösung

(1) Bei System B treten viermal die Metriken 0 und viermal die Metriken 1 auf. Dies weist auf $n(t) = 0$ hin, da sich sonst – wie bei den Systemen A und C – alle $I_i$ unterscheiden müssten.

(2) Beim System B ergeben sich folgende Entscheidungswerte $W_i = I_i \ – E_i/2$, jeweils normiert auf $E_{\rm B}$:

$$W_0 = 0 - 0 = 0, \hspace{0.2cm}W_1 = 0 - 0.5 = -0.5 \hspace{0.05cm},$$

$$W_2 = 1 - 0.5 = 0.5, \hspace{0.2cm}W_3 = 1 - 1 = 0 \hspace{0.05cm},$$

$$W_4 = 0 - 0.5 = -0.5, \hspace{0.2cm}W_5 = 0 - 1 = -1 \hspace{0.05cm}.$$

$$W_6 = 1 - 1 = 0, \hspace{0.2cm}W_7 = 1 - 1.5 = -0.5 \hspace{0.05cm}.$$

Der maximale Wert $W_2 = 0.5$ ⇒ $i = 2$. Der Korrelationsempfänger entscheidet sich also für $V = Q_2$. Da keine Störungen auftreten, wurde tatsächtlich auch $Q_2 = „010”$ gesendet ⇒ $k \ \underline {= 2}$.

(3) Für die Entscheidungswerte von System A gilt:

$$W_0 = 0.00 - 0.00 = 0.00, \hspace{0.2cm}W_1 = -0.07 - 0.50 = -0.57, $$

$$W_2 = 1.13 - 0.50 = 0.63, \hspace{0.2cm}W_3 = 1.06 - 1.00 = 0.06 \hspace{0.05cm},$$

$$W_4 = 0.05 - 0.50 = -0.45, \hspace{0.2cm}W_5 = -0.02 - 1.00 = -1.02 \hspace{0.05cm},$$

$$W_6 = 1.18 - 1.00 = 0.18, \hspace{0.2cm}W_7 = 1.11 - 1.50 = -0.39 \hspace{0.05cm}.$$

Das Maximum ist $W_j = W_2$ ⇒ $j \ \underline {= 2}$. Das heißt, dass der Korrelationsempfänger auch bei System A die richtige Entscheidung $V = Q_2$ trifft. Ohne den Korrekturterm ($– E_i/2$) hätte der Empfänger allerdings die falsche Entscheidung $V = Q_6$ getroffen.

(4) Der Korrelationsempfänger C hat folgende Werte zu vergleichen:

$$W_0 = 0.00 - 0.00 = 0.00, \hspace{0.2cm}W_1 = -1.31 - 0.50 = -1.81 \hspace{0.05cm},$$

$$W_2 = 3.59 - 0.50 = 3.09, \hspace{0.2cm}W_3 = 2.28 - 1.00 = 1.28 \hspace{0.05cm},$$

$$W_4 = 0.97 - 0.50 = 0.47, \hspace{0.2cm}W_5 = -0.34 - 1.00 = -1.34 \hspace{0.05cm},$$

$$W_6 = 4.56 - 1.00 = 3.56, \hspace{0.2cm}W_7 = 3.25 - 1.50 = 1.75 \hspace{0.05cm}.$$

Die Maximierung ergibt hier $\underline {j = 6}$ &8656; $V = Q_6$. Da aber $Q_2$ gesendet wurde, entscheidet hier der Korrelationsempfänger falsch. Die Störungen sind zu stark.

(5) Die Störungen sind bei System C am größten und für die aktuellen Empfangswerte sogar so groß, dass der Korrelationsempfänger eine Fehlentscheidung trifft.

(6) Die erste Aussage ist richtig. Im fehlerfreien Fall ist die Differenz zwischen $W_2 = 0.5$ und den nächstgrößten Werten $W_0 = W_3 = W_6 = 0$ jeweils gleich $0.5$. Bei System B (leichte Störungen) ist die Differenz zwischen $W_2 = 0.63$ und dem nächstgrößeren Wert $W_6 = 0.18$ immerhin noch $D_{\rm min} = 0.45$. Erhöht man die Rauschleistung um den Faktor 50, so entscheidet der Korrelationsempfänger immer noch richtig, doch ist dann die minimale Differenz $D_{\rm min} = 0.16$ deutlich kleiner.

Für das System C, bei dem der Korrelationsempfänger überfordert ist (siehe Teilaufgabe (4)), wurde eine gegenüber dem System A um den Faktor 400 größere Rauschleistung zugrundegelegt.

Entscheidet der Korrelationsempfänger die gesendete Folge $Q_2$ falsch, so ist eine Verfälschung zu den Folgen $Q_0$, $Q_3$ bzw. $Q_6$ am wahrscheinlichsten, da sich alle diese drei Folgen von $Q_2$ nur jeweils in einem Bit unterscheiden. Dass bei der beschriebenen Simulation $W_6$ stets größer ist als $W_0$ bzw. $W_3$, ist „Zufall” und sollte nicht überinterpretiert werden. Richtig sind also die Aussagen 1 und 3.