Aufgaben:Aufgabe 3.09: Grundlegendes zum Viterbi–Algorithmus: Unterschied zwischen den Versionen
K (Guenter verschob die Seite Aufgabe 3.09: Viterbi–Algorithmus: Grundlegendes nach Aufgabe 3.09: Grundlegendes zum Viterbi–Algorithmus) |
|||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
[[Datei:P_ID2659__KC_A_3_8.png|right|frame|Zu analysierendes Trellis]] | [[Datei:P_ID2659__KC_A_3_8.png|right|frame|Zu analysierendes Trellis]] | ||
| − | Die Grafik zeigt ein Trellisdiagramm und definiert gleichzeitig die Fehlergrößen ${\it \Gamma}_i(S_0)$ und ${\it \Gamma}_i(S_1)$ zu den | + | Die Grafik zeigt ein Trellisdiagramm und definiert gleichzeitig die Fehlergrößen ${\it \Gamma}_i(S_0)$ und ${\it \Gamma}_i(S_1)$ zu den Zeiten $i = 0$ bis $i = 5$. |
| − | * die Coderate $R$, | + | |
| − | * das Gedächtnis $m$, | + | Aus diesem Trellis können zum Beispiel abgelesen werden: |
| − | * die freie Distanz $d_{\rm F}$, | + | * die Coderate $R$, |
| − | * die Informationssequenzlänge $L$, | + | * das Gedächtnis $m$, |
| − | * die Sequenzlänge $L'$ inklusive der Terminierung. | + | * die freie Distanz $d_{\rm F}$, |
| + | * die Informationssequenzlänge $L$, | ||
| + | * die Sequenzlänge $L\hspace{0.05cm}'$ inklusive der Terminierung. | ||
In der Aufgabe ist weiter zu klären: | In der Aufgabe ist weiter zu klären: | ||
| − | * die Bedeutung des Endwertes ${\it \Gamma}_5(S_0)$, | + | * die Bedeutung des Endwertes ${\it \Gamma}_5(S_0)$, |
| − | * Auswirkungen von einem bzw. zwei Übertragungsfehlern. | + | * Auswirkungen von einem bzw. von zwei Übertragungsfehlern. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | '' | + | ''Hinweis:'' |
| − | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Decodierung_von_Faltungscodes| Decodierung von Faltungscodes]]. | + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Decodierung_von_Faltungscodes| Decodierung von Faltungscodes]]. |
| − | + | ||
| Zeile 30: | Zeile 38: | ||
|type="[]"} | |type="[]"} | ||
+ Es handelt sich um einen Rate–1/2–Faltungscode. | + Es handelt sich um einen Rate–1/2–Faltungscode. | ||
| − | - Das Gedächtnis des Codes ist $m = 2$. | + | - Das Gedächtnis des Codes ist $m = 2$. |
+ Der Faltungscode ist terminiert. | + Der Faltungscode ist terminiert. | ||
| − | - Die Länge der Informationssequenz ist $L = 5$. | + | - Die Länge der Informationssequenz ist $L = 5$. |
| − | {Geben Sie die freie Distanz $d_{\rm F}$ des Faltungscodes an. | + | {Geben Sie die freie Distanz $d_{\rm F}$ des Faltungscodes an. |
|type="{}"} | |type="{}"} | ||
$d_{\rm F} \ = \ ${ 3 3% } | $d_{\rm F} \ = \ ${ 3 3% } | ||
| − | {Welche Aussagen erlaubt der Endwert ${\it \Gamma}_5(S_0) = 0$ der Fehlergröße? | + | {Welche Aussagen erlaubt der Endwert ${\it \Gamma}_5(S_0) = 0$ der Fehlergröße? |
|type="[]"} | |type="[]"} | ||
- Es ist kein Übertragungsfehler aufgetreten. | - Es ist kein Übertragungsfehler aufgetreten. | ||
| − | - Das Decodierergebnis $\underline{ | + | - Das Decodierergebnis $\underline{v}$ ist mit Sicherheit richtig $($gleich $\underline{u})$. |
| − | + Das Decodierergebnis minimiert die Wahrscheinlichkeit ${\rm Pr}(\underline{ | + | + Das Decodierergebnis minimiert die Wahrscheinlichkeit ${\rm Pr}(\underline{v} ≠ \underline{u})$. |
{Welche Aussagen treffen <u>bei einem einzigen</u> Übertragungsfehler zu? | {Welche Aussagen treffen <u>bei einem einzigen</u> Übertragungsfehler zu? | ||
|type="[]"} | |type="[]"} | ||
| − | + Der Fehlergrößenendwert ist ${\it \Gamma}_5(S_0) = 1$. | + | + Der Fehlergrößenendwert ist ${\it \Gamma}_5(S_0) = 1$. |
| − | + Das Decodierergebnis $\underline{ | + | + Das Decodierergebnis $\underline{v}$ ist mit Sicherheit richtig $($gleich $\underline{u})$. |
| − | + Das Decodierergebnis minimiert die Wahrscheinlichkeit ${\rm Pr}(\underline{ | + | + Das Decodierergebnis minimiert die Wahrscheinlichkeit ${\rm Pr}(\underline{v} ≠ \underline{u})$. |
{Welche Aussagen treffen <u>bei zwei</u> Übertragungsfehlern zu? | {Welche Aussagen treffen <u>bei zwei</u> Übertragungsfehlern zu? | ||
|type="[]"} | |type="[]"} | ||
| − | - Der Fehlergrößenendwert ist ${\it \Gamma}_5(S_0) = 2$. | + | - Der Fehlergrößenendwert ist ${\it \Gamma}_5(S_0) = 2$. |
| − | - Das Decodierergebnis $\underline{ | + | - Das Decodierergebnis $\underline{v}$ ist mit Sicherheit richtig $($gleich $\underline{u})$. |
| − | - Das Decodierergebnis $\underline{ | + | - Das Decodierergebnis $\underline{v}$ ist mit Sicherheit falsch $($ungleich $\underline{u})$. |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u> | + | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: |
| + | *Es gibt hier $2^{k \cdot m} = 2$ Zustände. Daraus folgt $k = 1$ und $m = 1$. | ||
| + | *Pro Codierschritt werden $n = 2$ Codebits ausgegeben ⇒ $R = 1/2$. | ||
| + | *Die Informationssequenzlänge ist $L = 4$. | ||
| + | *Erst durch ein (da $m = 1$) zusätzliches Terminierungsbit kommt man zur Gesamtlänge $L' = 5$. | ||
| + | |||
| Zeile 65: | Zeile 78: | ||
:$$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$ | :$$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$ | ||
| − | ausgedrückt mit der Zustandsabfolge: $S_0 → S_0 → S_0 → S_0 → \ ... \ $ Eine der Folgen $\underline{x} ≠ \underline{0}$, die sich von $\underline{0}$ nur in der minimalen Anzahl an Codebits unterscheidet, folgt dem Pfad $S_0 → S_1 → S_0 → S_0 → \ ... \ $ : | + | ausgedrückt mit der Zustandsabfolge: $S_0 → S_0 → S_0 → S_0 → \ \text{...} \ $ |
| + | *Eine der Folgen $\underline{x} ≠ \underline{0}$, die sich von $\underline{0}$ nur in der minimalen Anzahl an Codebits unterscheidet, folgt dem Pfad $S_0 → S_1 → S_0 → S_0 → \\text{...} \ $: | ||
:$$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) | :$$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} | ||
| Zeile 71: | Zeile 85: | ||
| − | |||
| − | [[Datei:P_ID2660__KC_A_3_9c.png|center|frame|Trellis ohne Fehler/mit | + | '''(3)''' Richtig ist hier nur der <u>Vorschlag 3</u>, weil das Ereignis „Kein Übertragungsfehler” sehr viel wahrscheinlicher ist als drei Fehler an genau vorgegebenen Positionen. Betrachten Sie hierzu die folgende Grafik: |
| + | |||
| + | [[Datei:P_ID2660__KC_A_3_9c.png|center|frame|Trellis ohne Fehler/mit drei Übertragungsfehlern]] | ||
| + | |||
| + | *Wird die Nullsequenz gesendet und diese auch empfangen, so kann die Viterbi–Decodierung durch das obere Trellis veranschaulicht werden. | ||
| + | *Der Endwert der Fehlergröße ist ${\it \Gamma}_5(S_0) = 0$, und der Viterbi–Decoder entscheidet mit Sicherheit richtig: $\underline{z} = \underline{x} ⇒ \underline{v} = \underline{u}$. | ||
| + | *Für das untere Trellis gehen wir ebenfalls von $\underline{u} = (0, \, 0, \, 0, \, 0, \, 0) ⇒ \underline{x} = (00, \, 00, \, 00, \, 00, \, 00)$ aus. Empfangen wird aber nun $\underline{y} = (00, \, 00, \, 00, \, 11, \, 01)$. Trotzdem gilt ${\it \Gamma}_5(S_0) = 0$. Das Beispiel belegt, dass die beiden ersten Aussagen falsch sind. | ||
| + | |||
| − | |||
| + | '''(4)''' Richtig sind <u>alle Antworten</u>: | ||
| + | *Wenn man sicher weiß, dass nur ein Übertragungsfehler aufgetreten ist, funktioniert bei einem Faltungscode mit der freien Distanz $d_{\rm F} = 3$ der Viterbi–Algorithmus perfekt, egal, an welcher Position der Fehler aufgetreten ist. | ||
| − | |||
| − | '''(5)''' Keiner der Lösungsvorschläge ist richtig, wie aus den nachfolgenden Beispielen zu erkennen ist. | + | '''(5)''' <u> Keiner der Lösungsvorschläge</u> ist richtig, wie aus den nachfolgenden Beispielen zu erkennen ist. |
| − | [[Datei:P_ID2661__KC_A_3_9e.png|center|frame|Trellis mit | + | [[Datei:P_ID2661__KC_A_3_9e.png|center|frame|Trellis mit zwei Übertragungsfehlern]] |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 26. Juni 2019, 08:19 Uhr
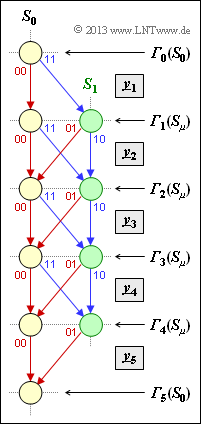
Die Grafik zeigt ein Trellisdiagramm und definiert gleichzeitig die Fehlergrößen ${\it \Gamma}_i(S_0)$ und ${\it \Gamma}_i(S_1)$ zu den Zeiten $i = 0$ bis $i = 5$.
Aus diesem Trellis können zum Beispiel abgelesen werden:
- die Coderate $R$,
- das Gedächtnis $m$,
- die freie Distanz $d_{\rm F}$,
- die Informationssequenzlänge $L$,
- die Sequenzlänge $L\hspace{0.05cm}'$ inklusive der Terminierung.
In der Aufgabe ist weiter zu klären:
- die Bedeutung des Endwertes ${\it \Gamma}_5(S_0)$,
- Auswirkungen von einem bzw. von zwei Übertragungsfehlern.
Hinweis:
- Die Aufgabe gehört zum Kapitel Decodierung von Faltungscodes.
Fragebogen
Musterlösung
- Es gibt hier $2^{k \cdot m} = 2$ Zustände. Daraus folgt $k = 1$ und $m = 1$.
- Pro Codierschritt werden $n = 2$ Codebits ausgegeben ⇒ $R = 1/2$.
- Die Informationssequenzlänge ist $L = 4$.
- Erst durch ein (da $m = 1$) zusätzliches Terminierungsbit kommt man zur Gesamtlänge $L' = 5$.
(2) Die freie Distanz $d_{\rm F}$ ist definiert als die Anzahl der Codebits, in denen sich zwei Sequenzen $\underline{x}$ und $\underline{x'}$ unterscheiden. Als Bezugssequenz wählen wir die Nullsequenz:
- $$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$
ausgedrückt mit der Zustandsabfolge: $S_0 → S_0 → S_0 → S_0 → \ \text{...} \ $
- Eine der Folgen $\underline{x} ≠ \underline{0}$, die sich von $\underline{0}$ nur in der minimalen Anzahl an Codebits unterscheidet, folgt dem Pfad $S_0 → S_1 → S_0 → S_0 → \\text{...} \ $:
- $$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} \hspace{0.05cm}.$$
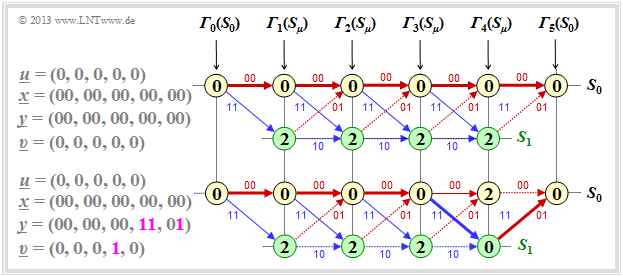
(3) Richtig ist hier nur der Vorschlag 3, weil das Ereignis „Kein Übertragungsfehler” sehr viel wahrscheinlicher ist als drei Fehler an genau vorgegebenen Positionen. Betrachten Sie hierzu die folgende Grafik:
- Wird die Nullsequenz gesendet und diese auch empfangen, so kann die Viterbi–Decodierung durch das obere Trellis veranschaulicht werden.
- Der Endwert der Fehlergröße ist ${\it \Gamma}_5(S_0) = 0$, und der Viterbi–Decoder entscheidet mit Sicherheit richtig: $\underline{z} = \underline{x} ⇒ \underline{v} = \underline{u}$.
- Für das untere Trellis gehen wir ebenfalls von $\underline{u} = (0, \, 0, \, 0, \, 0, \, 0) ⇒ \underline{x} = (00, \, 00, \, 00, \, 00, \, 00)$ aus. Empfangen wird aber nun $\underline{y} = (00, \, 00, \, 00, \, 11, \, 01)$. Trotzdem gilt ${\it \Gamma}_5(S_0) = 0$. Das Beispiel belegt, dass die beiden ersten Aussagen falsch sind.
(4) Richtig sind alle Antworten:
- Wenn man sicher weiß, dass nur ein Übertragungsfehler aufgetreten ist, funktioniert bei einem Faltungscode mit der freien Distanz $d_{\rm F} = 3$ der Viterbi–Algorithmus perfekt, egal, an welcher Position der Fehler aufgetreten ist.
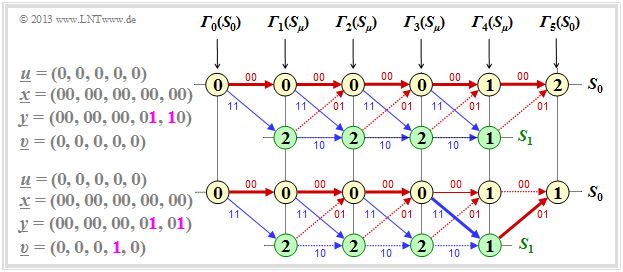
(5) Keiner der Lösungsvorschläge ist richtig, wie aus den nachfolgenden Beispielen zu erkennen ist.