Aufgaben:Aufgabe 2.7Z: ZSB-AM und Hüllkurvendemodulator: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 20: | Zeile 20: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {Schätzen Sie den maximalen Betrag des Quellensignals ab. | ||
| + | |type="{}"} | ||
| + | $q_{max} = max |q(t)|$ = { 4 3% } $V$ | ||
| − | { | + | {Wie groß ist die Amplitude $A_T$ des beim Sender zugesetzten Trägersignals? Welcher Modulationsgrad m ergibt sich hieraus? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_T$ = { 4 3% } $V$ |
| + | $m$ = { 1 3% } | ||
| + | {Was spricht hier für oder gegen die Verwendung eines Hüllkurvendemodulators (HKD)? Die Alternative wäre ein Synchrondemodulator (SD). | ||
| + | |type="[]"} | ||
| + | - Mit dem HKD ist keine verzerrungsfreie Demodulation möglich. | ||
| + | + Man kann auf die Frequenz–/Phasensynchronisation verzichten. | ||
| + | + Mit einem SD würde eine kleinere Sendeleistung genügen. | ||
| + | {Berechnen Sie durch Fourierrücktransformation von $R_{TP}(f)$ das äquivalente TP–Signal $r_{TP}(t)$ ⇒ „Ortskurve”. Welche Aussagen treffen zu? | ||
| + | |type="[]"} | ||
| + | + Die Ortskurve rTP(t) setzt sich aus fünf Zeigern zusammen. | ||
| + | - Der Träger rotiert mit der Drehgeschwindigkeit $ω_T$. | ||
| + | + Die Drehzeiger der negativen Frequenzen drehen im Uhrzeigersinn. | ||
| + | - Der Zeiger für 2 kHz dreht doppelt so schnell als der für 5 kHz. | ||
| + | { Welche Aussagen sind anhand der Ortskurve möglich? Beantworten Sie hierzu folgende Fragen hinsichtlich der Anwendung von Hüllkurvendemodulation. | ||
| + | |type="[]"} | ||
| + | + Eine verzerrungsfreie Demodulation ist nur möglich, wenn $r_TP(t)$ für alle Zeiten reell ist. | ||
| + | + Eine verzerrungsfreie Demodulation ist nur möglich, wenn $r_TP(t)$ zu keinem Zeitpunkt negativ wird. | ||
| + | - Sind die beiden erstgenannten Bedingungen nicht erfüllt, so komt es zu linearen Verzerrungen. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
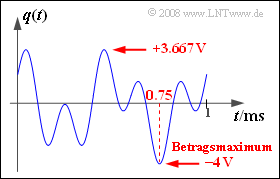
| − | '''1.''' | + | '''1.''' Die folgende Grafik zeigt, dass das Quellensignal alle Werte zwischen –4 V und +3.667 V annehmen kann. Der maximale Betrag tritt zum Beispiel zum Zeitpunkt t = 0.75 ms auf: |
| − | '''2.''' | + | $$q(t = 0.75 \,{\rm ms}) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot 0.75 \,{\rm ms} ) + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot 0.75 \,{\rm ms} )$$ |
| − | '''3.''' | + | $$ = 2 \,{\rm V} \cdot \cos(3 \pi) + 2 \,{\rm V} \cdot \sin(7.5 \pi)= -4 \,{\rm V}\hspace{0.05cm}.$$ |
| − | '''4.''' | + | [[Datei:P_ID1035__Mod_Z_2_7_a.png|right|]] |
| − | '''5.''' | + | Daraus folgt $q_{max} = 4 V$. |
| − | + | ||
| − | + | ||
| + | '''2.''' In der Grafik auf der Angabenseite gibt das Gewicht der Diraclinie bei $f = 0$ die Amplitude des zugesetzten Trägers an. Diese ist $A_T = 4 V$. Daraus erhält man den Modulationsgrad $m = q_{max}/A_T = 1$. | ||
| + | |||
| + | |||
| + | '''3.'''Da der Modulationsgrad nicht größer als 1 ist, führt auch der Hüllkurvendemodulator (HKD) nicht zu Verzerrungen. Der wesentliche Vorteil der HKD ist, dass keine Frequenz– und Phasensynchronität notwendig ist. Nachteilig ist, dass im Gegensatz zur Synchrondemodulation beim Sender eine deutlich höhere Leistung aufgebracht werden muss. Bei m = 1 ergibt sich gegenüber der ZSB–AM ohne Träger die dreifache Sendeleistung. Richtig sind also die Lösungsvorschläge 2 und 3. | ||
| + | |||
| + | |||
| + | [[Datei:P_ID1036__Mod_Z_2_7_d.png|right|]] | ||
| + | '''4.''' Mit $ω_2 = 2 π · 2 kHz$ und $ω_5 = 2 π · 5 kHz$ gilt: | ||
| + | $$ r_{\rm TP}(t) = 4 \,{\rm V} + 1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} + 1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t}$$ | ||
| + | $$- \hspace{0.15cm}{\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} + {\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{0.05cm}. \hspace{0.1cm}$$ | ||
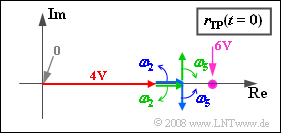
| + | Bei der Konstruktion der Ortskurve $r_{TP}(t)$ sind somit genau fünf Zeiger zu berücksichtigen. Die Grafik zeigt eine Momentanaufnahme zum Zeitpunkt t = 0. | ||
| + | |||
| + | Der (rote) Träger ist für alle Zeiten durch den reellen Zeiger der Länge 4 V gegeben. Im Gegensatz zum Zeigerdiagramm (Darstellung des analytischen Signals) dreht dieser nicht. | ||
| + | |||
| + | Die dritte Aussage ist ebenso wie die Aussage 1 richtig: Die Drehzeiger bei negativen Frequenzen drehen in mathematisch negativer Richtung (im Uhrzeigersinn) im Gegensatz zu den beiden Zeigern mit f > 0. Die Aussagen 2 und 4 treffen dagegen nicht zu. | ||
| + | |||
| + | [[Datei:P_ID1037__Mod_Z_2_7_e.png|right|]] | ||
| + | '''5.'''Im betrachteten Beispiel kann für das äquivalente TP–Signal auch geschrieben werden: | ||
| + | $$r_{\rm TP}(t) = q(t) + A_{\rm T} \hspace{0.05cm}.$$ | ||
| + | Damit ist offensichtlich, dass $r_{TP}(t)$ stets reell ist. Aus a) und b) folgt weiter $r_{TP}(t) ≥ 0$ ist. | ||
| + | Das bedeutet: | ||
| + | |||
| + | |||
| + | Die Ortskurve ist hier eine horizontale Gerade auf der reellen Gerade und liegt stets in der rechten Halbebene. Dies sind die beiden notwendigen Bedingungen, dass mit einem Hüllkurvendemodulator das Nachrichtensignal verzerrungsfrei wiedergewonnen werden kann. Ist eine dieser Voraussetzungen nicht erfüllt, so kommt es zu $\text{nichtlinearen}$ Verzerrungen. Das bedeutet, dass der letzte Lösungsvorschlag falsch ist. Richtig sind dagegen die Aussagen 1 und 2. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 1. Januar 2017, 20:00 Uhr
Ausgegangen wird vom Quellensignal $$ q(t) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t ) +$$ $$ + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm}.$$ Dieses wird entsprechend dem Modulationsverfahren „ZSB–AM mit Träger” moduliert und über einen idealen Kanal übertragen. Der Einfluss von Rauschen kann außer Acht gelassen werden.
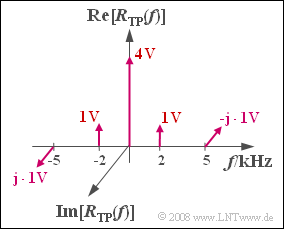
Die nebenstehende Grafik zeigt das Spektrum $R_{TP}(f)$ des Empfangssignals im äquivalenten Tiefpassbereich, das sich aus Diraclinien bei $f = 0$ (herrührend vom Träger), bei $±2 kHz$ (herrührend vom Cosinusanteil) und bei $±5 kHz$ (herrührend vom Sinusanteil) zusammensetzt.
Als Ortskurve bezeichnet man die Darstellung des äquivalenten Tiefpass–Signals $r_{TP}(t)$ in der komplexen Ebene, wobei $r_{TP}(t)$ die Fourierrücktransformierte von $R_{TP}(f)$ angibt.
Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 2.3
Fragebogen
Musterlösung
Daraus folgt $q_{max} = 4 V$.
2. In der Grafik auf der Angabenseite gibt das Gewicht der Diraclinie bei $f = 0$ die Amplitude des zugesetzten Trägers an. Diese ist $A_T = 4 V$. Daraus erhält man den Modulationsgrad $m = q_{max}/A_T = 1$.
3.Da der Modulationsgrad nicht größer als 1 ist, führt auch der Hüllkurvendemodulator (HKD) nicht zu Verzerrungen. Der wesentliche Vorteil der HKD ist, dass keine Frequenz– und Phasensynchronität notwendig ist. Nachteilig ist, dass im Gegensatz zur Synchrondemodulation beim Sender eine deutlich höhere Leistung aufgebracht werden muss. Bei m = 1 ergibt sich gegenüber der ZSB–AM ohne Träger die dreifache Sendeleistung. Richtig sind also die Lösungsvorschläge 2 und 3.
4. Mit $ω_2 = 2 π · 2 kHz$ und $ω_5 = 2 π · 5 kHz$ gilt: $$ r_{\rm TP}(t) = 4 \,{\rm V} + 1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} + 1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t}$$ $$- \hspace{0.15cm}{\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} + {\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{0.05cm}. \hspace{0.1cm}$$ Bei der Konstruktion der Ortskurve $r_{TP}(t)$ sind somit genau fünf Zeiger zu berücksichtigen. Die Grafik zeigt eine Momentanaufnahme zum Zeitpunkt t = 0.
Der (rote) Träger ist für alle Zeiten durch den reellen Zeiger der Länge 4 V gegeben. Im Gegensatz zum Zeigerdiagramm (Darstellung des analytischen Signals) dreht dieser nicht.
Die dritte Aussage ist ebenso wie die Aussage 1 richtig: Die Drehzeiger bei negativen Frequenzen drehen in mathematisch negativer Richtung (im Uhrzeigersinn) im Gegensatz zu den beiden Zeigern mit f > 0. Die Aussagen 2 und 4 treffen dagegen nicht zu.
5.Im betrachteten Beispiel kann für das äquivalente TP–Signal auch geschrieben werden: $$r_{\rm TP}(t) = q(t) + A_{\rm T} \hspace{0.05cm}.$$ Damit ist offensichtlich, dass $r_{TP}(t)$ stets reell ist. Aus a) und b) folgt weiter $r_{TP}(t) ≥ 0$ ist. Das bedeutet:
Die Ortskurve ist hier eine horizontale Gerade auf der reellen Gerade und liegt stets in der rechten Halbebene. Dies sind die beiden notwendigen Bedingungen, dass mit einem Hüllkurvendemodulator das Nachrichtensignal verzerrungsfrei wiedergewonnen werden kann. Ist eine dieser Voraussetzungen nicht erfüllt, so kommt es zu $\text{nichtlinearen}$ Verzerrungen. Das bedeutet, dass der letzte Lösungsvorschlag falsch ist. Richtig sind dagegen die Aussagen 1 und 2.