Aufgaben:Aufgabe 2.7Z: ZSB-AM und Hüllkurvendemodulator: Unterschied zwischen den Versionen
| Zeile 64: | Zeile 64: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[Datei:P_ID1035__Mod_Z_2_7_a.png|right|frame|Quellensignal im Bereich bis $1\text{ ms}$]] | + | [[Datei:P_ID1035__Mod_Z_2_7_a.png|right|frame|Quellensignal im Bereich bis $1\text{ ms}$]] |
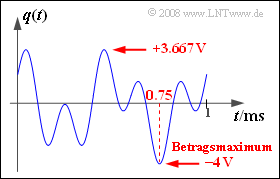
| − | '''(1)''' Die Grafik zeigt, dass das Quellensignal alle Werte zwischen $–4 \ \rm V$ und $+3.667\ \rm V$ annehmen kann. | + | '''(1)''' Die Grafik zeigt, dass das Quellensignal alle Werte zwischen $–4 \ \rm V$ und $+3.667\ \rm V$ annehmen kann. |
| − | *Der maximale Betrag tritt zum Beispiel zum Zeitpunkt $t = t_0 =0.75\ \rm ms$ auf: | + | *Der maximale Betrag tritt zum Beispiel zum Zeitpunkt $t = t_0 =0.75\ \rm ms$ auf: |
:$$q(t = t_0) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t_0 ) + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t_0 )$$ | :$$q(t = t_0) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t_0 ) + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t_0 )$$ | ||
:$$\Rightarrow \hspace{0.3cm}q(t = 0.75 \,{\rm ms}) = 2 \,{\rm V} \cdot \cos(3 \pi) + 2 \,{\rm V} \cdot \sin(7.5 \pi)= -4 \,{\rm V}\hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm}q(t = 0.75 \,{\rm ms}) = 2 \,{\rm V} \cdot \cos(3 \pi) + 2 \,{\rm V} \cdot \sin(7.5 \pi)= -4 \,{\rm V}\hspace{0.05cm}.$$ | ||
| − | Daraus folgt für den maximalen Betrag: $q_{\rm max}\hspace{0.15cm}\underline{ = 4 \ \rm V}$. | + | *Daraus folgt für den maximalen Betrag: $q_{\rm max}\hspace{0.15cm}\underline{ = 4 \ \rm V}$. |
| − | '''(2)''' In der Angabenseite–Grafik gibt das Gewicht der Diraclinie bei $f = 0$ die Amplitude des zugesetzten Trägers an. | + | |
| − | *Diese ist $A_{\rm T}\hspace{0.15cm}\underline{ = 4\ \rm V }$. | + | '''(2)''' In der Angabenseite–Grafik gibt das Gewicht der Diraclinie bei $f = 0$ die Amplitude des zugesetzten Trägers an. |
| − | *Daraus erhält man den Modulationsgrad $m = q_{\rm max}/A_{\rm T} \hspace{0.15cm}\underline{ = 1}$. | + | *Diese ist $A_{\rm T}\hspace{0.15cm}\underline{ = 4\ \rm V }$. |
| + | *Daraus erhält man den Modulationsgrad $m = q_{\rm max}/A_{\rm T} \hspace{0.15cm}\underline{ = 1}$. | ||
| + | |||
'''(3)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | '''(3)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | ||
| − | *Da der Modulationsgrad nicht größer als $m = 1$ ist, führt auch der Hüllkurvendemodulator nicht zu Verzerrungen. | + | *Da der Modulationsgrad nicht größer als $m = 1$ ist, führt auch der Hüllkurvendemodulator nicht zu Verzerrungen. |
*Der wesentliche Vorteil der Hüllkurvendemodulation ist, dass keine Frequenz– und Phasensynchronität notwendig ist. | *Der wesentliche Vorteil der Hüllkurvendemodulation ist, dass keine Frequenz– und Phasensynchronität notwendig ist. | ||
*Nachteilig ist, dass im Gegensatz zur Synchrondemodulation beim Sender eine deutlich höhere Leistung aufgebracht werden muss. | *Nachteilig ist, dass im Gegensatz zur Synchrondemodulation beim Sender eine deutlich höhere Leistung aufgebracht werden muss. | ||
| − | *Bei $m = 1$ ergibt sich gegenüber der ZSB–AM ohne Träger die dreifache Sendeleistung. | + | *Bei $m = 1$ ergibt sich gegenüber der ZSB–AM ohne Träger die dreifache Sendeleistung. |
| + | |||
| − | [[Datei:P_ID1036__Mod_Z_2_7_d.png|right|frame|Äquivalentes Tiefpass–Signal in der komplexen Ebene]] | + | [[Datei:P_ID1036__Mod_Z_2_7_d.png|right|frame|Äquivalentes Tiefpass–Signal <br>in der komplexen Ebene]] |
'''(4)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | '''(4)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | ||
| − | *Mit $ω_2 = 2 π · 2 \ \rm kHz$ und $ω_5 = 2 π · \ \rm 5 kHz$ gilt: | + | *Mit $ω_2 = 2 π · 2 \ \rm kHz$ und $ω_5 = 2 π · \ \rm 5 kHz$ gilt: |
:$$ r_{\rm TP}(t) = 4 \,{\rm V} \hspace{-0.05cm}+\hspace{-0.05cm} 1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}+\hspace{-0.05cm} 1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} | :$$ r_{\rm TP}(t) = 4 \,{\rm V} \hspace{-0.05cm}+\hspace{-0.05cm} 1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}+\hspace{-0.05cm} 1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} | ||
\hspace{-0.05cm}-\hspace{-0.05cm} \hspace{0.15cm}{\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}+\hspace{-0.05cm} {\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{0.05cm}. \hspace{0.1cm}$$ | \hspace{-0.05cm}-\hspace{-0.05cm} \hspace{0.15cm}{\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}+\hspace{-0.05cm} {\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{0.05cm}. \hspace{0.1cm}$$ | ||
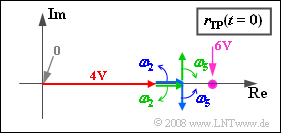
| − | *Bei der Konstruktion der Ortskurve $r_{TP}(t)$ sind somit genau fünf Zeiger zu berücksichtigen ⇒ Antwort 1 ist richtig. Die Grafik zeigt eine Momentaufnahme zum Zeitpunkt $t = 0$. | + | *Bei der Konstruktion der Ortskurve $r_{TP}(t)$ sind somit genau fünf Zeiger zu berücksichtigen ⇒ Antwort 1 ist richtig. Die Grafik zeigt eine Momentaufnahme zum Zeitpunkt $t = 0$. |
| − | *Der (rote) Träger ist für alle Zeiten durch den reellen Zeiger der Länge $4 \ \rm V$ gegeben. Im Gegensatz zum Zeigerdiagramm (Darstellung des analytischen Signals) dreht dieser nicht ⇒ Antwort 2 ist falsch. | + | :*Der (rote) Träger ist für alle Zeiten durch den reellen Zeiger der Länge $4 \ \rm V$ gegeben. Im Gegensatz zum Zeigerdiagramm (Darstellung des analytischen Signals) dreht dieser nicht ⇒ Antwort 2 ist falsch. |
| − | *Die dritte Aussage ist ebenso wie die Aussage 1 richtig: Die Drehzeiger bei negativen Frequenzen drehen in mathematisch negativer Richtung (im Uhrzeigersinn) im Gegensatz zu den beiden Zeigern mit $f > 0$. | + | :*Die dritte Aussage ist ebenso wie die Aussage 1 richtig: Die Drehzeiger bei negativen Frequenzen drehen in mathematisch negativer Richtung (im Uhrzeigersinn) im Gegensatz zu den beiden Zeigern mit $f > 0$. |
| − | *Die letzte Aussage trifft | + | :*Die letzte Aussage trifft nicht zu. Je größer die Frequenz $f$ ist, um so schneller dreht der zugehörige Zeiger. |
| Zeile 99: | Zeile 102: | ||
'''(5)''' Richtig sind die <u>Aussagen 1 und 2</u>: | '''(5)''' Richtig sind die <u>Aussagen 1 und 2</u>: | ||
| − | Im betrachteten Beispiel kann für das äquivalente TP–Signal auch geschrieben werden: | + | *Im betrachteten Beispiel kann für das äquivalente TP–Signal auch geschrieben werden: |
:$$r_{\rm TP}(t) = q(t) + A_{\rm T} \hspace{0.05cm}.$$ | :$$r_{\rm TP}(t) = q(t) + A_{\rm T} \hspace{0.05cm}.$$ | ||
| − | Damit ist offensichtlich, dass $r_{\rm TP}(t)$ stets reell ist. Aus den Teilaufgaben '''(1)''' und '''(2)''' folgt zudem $r_{\rm TP}(t) ≥ 0$. | + | *Damit ist offensichtlich, dass $r_{\rm TP}(t)$ stets reell ist. Aus den Teilaufgaben '''(1)''' und '''(2)''' folgt zudem $r_{\rm TP}(t) ≥ 0$. |
| + | |||
Das bedeutet: | Das bedeutet: | ||
| − | *Die Ortskurve ist hier eine horizontale Gerade auf der reellen Gerade und liegt stets in der rechten Halbebene. | + | :*Die Ortskurve ist hier eine horizontale Gerade auf der reellen Gerade und liegt stets in der rechten Halbebene. |
| − | *Dies sind die beiden notwendigen Bedingungen, dass mit einem Hüllkurvendemodulator das Nachrichtensignal verzerrungsfrei wiedergewonnen werden kann. | + | :*Dies sind die beiden notwendigen Bedingungen, dass mit einem Hüllkurvendemodulator das Nachrichtensignal verzerrungsfrei wiedergewonnen werden kann. |
| − | *Ist eine dieser Voraussetzungen nicht erfüllt, so kommt es zu <u>nichtlinearen</u> Verzerrungen, nicht zu linearen ⇒ Antwort 3 ist falsch. | + | :*Ist eine dieser Voraussetzungen nicht erfüllt, so kommt es zu <u>'''nichtlinearen'''</u> Verzerrungen, nicht zu linearen ⇒ Antwort 3 ist falsch. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 11. März 2020, 18:48 Uhr
Ausgegangen wird vom Quellensignal
- $$ q(t) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t ) + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm}.$$
Dieses wird entsprechend dem Modulationsverfahren „ZSB–AM mit Träger” moduliert und über einen idealen Kanal übertragen. Der Einfluss von Rauschen kann außer Acht gelassen werden.
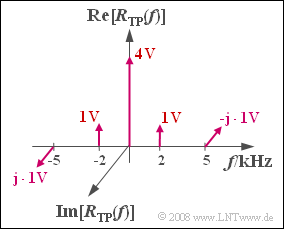
Die Grafik zeigt das Spektrum $R_{\rm TP}(f)$ des Empfangssignals im äquivalenten Tiefpassbereich, das sich aus Diraclinien bei $f = 0$ (herrührend vom Träger), bei $±2\ \rm kHz$ (herrührend vom Cosinusanteil) und bei $±5\ \rm kHz$ (herrührend vom Sinusanteil) zusammensetzt.
- Als Ortskurve bezeichnet man die Darstellung des äquivalenten Tiefpass–Signals $r_{\rm TP}(t)$ in der komplexen Ebene,
- wobei $r_{\rm TP}(t)$ die Fourierrücktransformierte von $R_{\ \rm TP}(f)$ angibt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Hüllkurvendemodulation.
- Bezug genommen wird insbesondere auf das Kapitel Beschreibung mit Hilfe des äquivalenten Tiefpass-Signals.
Fragebogen
Musterlösung
(1) Die Grafik zeigt, dass das Quellensignal alle Werte zwischen $–4 \ \rm V$ und $+3.667\ \rm V$ annehmen kann.
- Der maximale Betrag tritt zum Beispiel zum Zeitpunkt $t = t_0 =0.75\ \rm ms$ auf:
- $$q(t = t_0) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t_0 ) + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t_0 )$$
- $$\Rightarrow \hspace{0.3cm}q(t = 0.75 \,{\rm ms}) = 2 \,{\rm V} \cdot \cos(3 \pi) + 2 \,{\rm V} \cdot \sin(7.5 \pi)= -4 \,{\rm V}\hspace{0.05cm}.$$
- Daraus folgt für den maximalen Betrag: $q_{\rm max}\hspace{0.15cm}\underline{ = 4 \ \rm V}$.
(2) In der Angabenseite–Grafik gibt das Gewicht der Diraclinie bei $f = 0$ die Amplitude des zugesetzten Trägers an.
- Diese ist $A_{\rm T}\hspace{0.15cm}\underline{ = 4\ \rm V }$.
- Daraus erhält man den Modulationsgrad $m = q_{\rm max}/A_{\rm T} \hspace{0.15cm}\underline{ = 1}$.
(3) Richtig sind die Lösungsvorschläge 2 und 3:
- Da der Modulationsgrad nicht größer als $m = 1$ ist, führt auch der Hüllkurvendemodulator nicht zu Verzerrungen.
- Der wesentliche Vorteil der Hüllkurvendemodulation ist, dass keine Frequenz– und Phasensynchronität notwendig ist.
- Nachteilig ist, dass im Gegensatz zur Synchrondemodulation beim Sender eine deutlich höhere Leistung aufgebracht werden muss.
- Bei $m = 1$ ergibt sich gegenüber der ZSB–AM ohne Träger die dreifache Sendeleistung.
(4) Richtig sind die Lösungsvorschläge 1 und 3:
- Mit $ω_2 = 2 π · 2 \ \rm kHz$ und $ω_5 = 2 π · \ \rm 5 kHz$ gilt:
- $$ r_{\rm TP}(t) = 4 \,{\rm V} \hspace{-0.05cm}+\hspace{-0.05cm} 1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}+\hspace{-0.05cm} 1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}-\hspace{-0.05cm} \hspace{0.15cm}{\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}+\hspace{-0.05cm} {\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{0.05cm}. \hspace{0.1cm}$$
- Bei der Konstruktion der Ortskurve $r_{TP}(t)$ sind somit genau fünf Zeiger zu berücksichtigen ⇒ Antwort 1 ist richtig. Die Grafik zeigt eine Momentaufnahme zum Zeitpunkt $t = 0$.
- Der (rote) Träger ist für alle Zeiten durch den reellen Zeiger der Länge $4 \ \rm V$ gegeben. Im Gegensatz zum Zeigerdiagramm (Darstellung des analytischen Signals) dreht dieser nicht ⇒ Antwort 2 ist falsch.
- Die dritte Aussage ist ebenso wie die Aussage 1 richtig: Die Drehzeiger bei negativen Frequenzen drehen in mathematisch negativer Richtung (im Uhrzeigersinn) im Gegensatz zu den beiden Zeigern mit $f > 0$.
- Die letzte Aussage trifft nicht zu. Je größer die Frequenz $f$ ist, um so schneller dreht der zugehörige Zeiger.
(5) Richtig sind die Aussagen 1 und 2:
- Im betrachteten Beispiel kann für das äquivalente TP–Signal auch geschrieben werden:
- $$r_{\rm TP}(t) = q(t) + A_{\rm T} \hspace{0.05cm}.$$
- Damit ist offensichtlich, dass $r_{\rm TP}(t)$ stets reell ist. Aus den Teilaufgaben (1) und (2) folgt zudem $r_{\rm TP}(t) ≥ 0$.
Das bedeutet:
- Die Ortskurve ist hier eine horizontale Gerade auf der reellen Gerade und liegt stets in der rechten Halbebene.
- Dies sind die beiden notwendigen Bedingungen, dass mit einem Hüllkurvendemodulator das Nachrichtensignal verzerrungsfrei wiedergewonnen werden kann.
- Ist eine dieser Voraussetzungen nicht erfüllt, so kommt es zu nichtlinearen Verzerrungen, nicht zu linearen ⇒ Antwort 3 ist falsch.