Aufgaben:Aufgabe 2.7: Nochmals Zweiwegekanal: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID914__LZI_A_2_7.png|right|frame|Betragsfrequenzgang und Phasenfunktion des Zweiwegekanals]] | [[Datei:P_ID914__LZI_A_2_7.png|right|frame|Betragsfrequenzgang und Phasenfunktion des Zweiwegekanals]] | ||
| − | Wie in [[Aufgaben:2.6_Zweiwegekanal|Aufgabe 2.6]] wird ein Zweiwegekanal betrachtet, für dessen Impulsantwort gelte: | + | Wie in [[Aufgaben:2.6_Zweiwegekanal|Aufgabe 2.6]] wird ein Zweiwegekanal betrachtet, für dessen Impulsantwort gelte: |
:$$h(t) = \delta ( t - T_1) + \delta ( t - T_2).$$ | :$$h(t) = \delta ( t - T_1) + \delta ( t - T_2).$$ | ||
| − | Entgegen der allgemeinen Darstellung in Aufgabe 2.6 sind hier die beiden Dämpfungsfaktoren gleich: $z_1 = z_2 = 1$. Dies entspricht zum Beispiel beim Mobilfunk einem Echo im Abstand $T_2 - T_1$ in gleicher Stärke wie das Signal auf dem Hauptpfad. Für dieses wird die Laufzeit $T_1$ vorausgesetzt. | + | Entgegen der allgemeinen Darstellung in Aufgabe 2.6 sind hier die beiden Dämpfungsfaktoren gleich: $z_1 = z_2 = 1$. |
| + | *Dies entspricht zum Beispiel beim Mobilfunk einem Echo im Abstand $T_2 - T_1$ in gleicher Stärke wie das Signal auf dem Hauptpfad. | ||
| + | *Für dieses wird die Laufzeit $T_1$ vorausgesetzt. | ||
| − | Mit den in den Teilaufgaben (1) ... (4) betrachteten Laufzeiten $T_1 = 0$ und $T_2 = T = 4 \ \rm ms$ erhält man für den Frequenzgang des Zweiwegekanals, dessen Betrag in der oberen Grafik dargestellt ist: | + | |
| + | Mit den in den Teilaufgaben '''(1)''' ... '''(4)''' betrachteten Laufzeiten $T_1 = 0$ und $T_2 = T = 4 \ \rm ms$ erhält man für den Frequenzgang des Zweiwegekanals, dessen Betrag in der oberen Grafik dargestellt ist: | ||
:$$H(f) = 1 + {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f T} = 1 + | :$$H(f) = 1 + {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f T} = 1 + | ||
\cos(2 \pi f T) - {\rm j} \cdot \sin(2 \pi f T)$$ | \cos(2 \pi f T) - {\rm j} \cdot \sin(2 \pi f T)$$ | ||
| Zeile 15: | Zeile 18: | ||
T)\right)}= 2 \cdot |\cos(\pi f T)|.$$ | T)\right)}= 2 \cdot |\cos(\pi f T)|.$$ | ||
| − | Die untere Grafik zeigt die Phasenfunktion: | + | Die untere Grafik zeigt die Phasenfunktion für $T_1 = 0$ und $T_2 = T = 4 \ \rm ms$: |
:$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) = \arctan \frac{\sin(2 \pi f | :$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) = \arctan \frac{\sin(2 \pi f | ||
| − | T)}{1 + \cos(2 \pi f T)} = \arctan \ | + | T)}{1 + \cos(2 \pi f T)} = \arctan \big[\tan(\pi f T)\big].$$ |
| − | Hierbei wurde folgende trigonometrische Umformung benutzt: | + | *Im Frequenzbereich $|f| < 1/(2T)$ steigt $b(f)$ linear an: $b(f) = \pi \cdot f \cdot T.$ |
| + | *Auch in den weiteren Abschnitten der Phasenfunktion nimmt die Phase stets von $-\pi/2$ bis $+\pi/2$ linear zu. | ||
| + | *Hierbei wurde folgende trigonometrische Umformung benutzt: | ||
:$$ \frac{\sin(2 \alpha)}{1 + \cos(2 \alpha)} = \tan(\alpha).$$ | :$$ \frac{\sin(2 \alpha)}{1 + \cos(2 \alpha)} = \tan(\alpha).$$ | ||
| − | + | Im Fragenkatalog bezeichnet $y_i(t)$ das Signal am Ausgang des Zweiwegekanals, wenn am Eingang das Signal $x_i(t)$ anliegt $( i = 1, 2, 3, 4)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Als Eingangssignale werden untersucht: | Als Eingangssignale werden untersucht: | ||
| − | *ein Rechteckimpuls $x_1(t)$ mit | + | *ein Rechteckimpuls $x_1(t)$ mit Höhe $1$ zwischen $t= 0$ und $t= T$; für $t < 0$ und $t > T$ ist $x_1(t) = 0$ $($an den beiden Sprungstellen tritt jeweils der Wert $0.5$ auf$)$; |
| − | *ein Rechteckimpuls $x_2(t)$ mit Höhe $1$ im Bereich von $0 ... 2T$; | + | *ein Rechteckimpuls $x_2(t)$ mit Höhe $1$ im Bereich von $0 \ \text{...} \ 2T$; |
| − | *ein periodisches Rechtecksignal $x_3(t)$ mit der Periodendauer $T = T_0$: | + | *ein periodisches Rechtecksignal $x_3(t)$ mit der Periodendauer $T = T_0$: |
:$$x_3(t) = \left\{ \begin{array}{c} 1 \\ | :$$x_3(t) = \left\{ \begin{array}{c} 1 \\ | ||
0 \\ \end{array} \right.\quad \quad | 0 \\ \end{array} \right.\quad \quad | ||
| Zeile 40: | Zeile 40: | ||
{ T/2 < t < T,} \\ | { T/2 < t < T,} \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | *ein periodisches Rechtecksignal $x_4(t)$ mit der Periodendauer $T = 2T_0$: | + | *ein periodisches Rechtecksignal $x_4(t)$ mit der Periodendauer $T = 2T_0$: |
:$$x_4(t) = \left\{ \begin{array}{c} 1 \\ | :$$x_4(t) = \left\{ \begin{array}{c} 1 \\ | ||
0 \\ \end{array} \right.\quad \quad | 0 \\ \end{array} \right.\quad \quad | ||
| Zeile 53: | Zeile 53: | ||
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Lineare_Verzerrungen|Lineare Verzerrungen]]. | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Lineare_Verzerrungen|Lineare Verzerrungen]]. |
| − | *Für die Teilaufgaben (1) bis (4) gelte $T_1 = 0$ und $T_2 = T = 4 \ \rm ms$. In Teilaufgabe (5) wird der Fall $T_1 = 1 \ \rm ms$ und $T_2 = 5 \ \rm ms$ betrachtet. | + | *Für die Teilaufgaben '''(1)''' bis '''(4)''' gelte $T_1 = 0$ und $T_2 = T = 4 \ \rm ms$. |
| − | + | *In Teilaufgabe '''(5)''' wird der Fall $T_1 = 1 \ \rm ms$ und $T_2 = 5 \ \rm ms$ betrachtet. | |
| + | |||
| Zeile 63: | Zeile 64: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie das Ausgangssignal $y_1(t)$ für das Eingangssignal $x_1(t)$. Welche der Aussagen sind zutreffend? | + | {Berechnen Sie das Ausgangssignal $y_1(t)$ für das Eingangssignal $x_1(t)$. Welche der Aussagen sind zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | + $y_1(t)$ ist wie $x_1(t)$ rechteckförmig. | + | + $y_1(t)$ ist wie $x_1(t)$ rechteckförmig. |
| − | - $y_1(t)$ ist dreieckförmig. | + | - $y_1(t)$ ist dreieckförmig. |
| − | + Die absolute Impulsdauer ist $2T$. | + | + Die absolute Impulsdauer ist $2T$. |
| − | + $y_1(t)$ weist gegenüber $x_1(t)$ Dämpfungsverzerrungen auf. | + | + $y_1(t)$ weist gegenüber $x_1(t)$ Dämpfungsverzerrungen auf. |
| − | + $y_1(t)$ weist gegenüber $x_1(t)$ Phasenverzerrungen auf. | + | + $y_1(t)$ weist gegenüber $x_1(t)$ Phasenverzerrungen auf. |
| − | {Berechnen Sie das Signal $y_2(t)$. Welche Werte ergeben sich zu den Zeitpunkten $t= 0.5 T$, $t= 1.5 T$ und $t= 2.5 T$? | + | {Berechnen Sie das Signal $y_2(t)$. Welche Werte ergeben sich zu den Zeitpunkten $t= 0.5 T$, $t= 1.5 T$ und $t= 2.5 T$? |
|type="{}"} | |type="{}"} | ||
$y_2(t = 0.5T) \ = \ $ { 1 3% } | $y_2(t = 0.5T) \ = \ $ { 1 3% } | ||
| Zeile 79: | Zeile 80: | ||
| − | {Berechnen Sie das Signal $y_3(t)$. Überprüfen Sie, welche Aussagen zutreffen. | + | {Berechnen Sie das Signal $y_3(t)$. Überprüfen Sie, welche Aussagen zutreffen. |
|type="[]"} | |type="[]"} | ||
| − | + $y_3(t)$ ist gegenüber $x_3(t)$ unverzerrt. | + | + $y_3(t)$ ist gegenüber $x_3(t)$ unverzerrt. |
| − | - $y_3(t)$ weist gegenüber $x_3(t)$ Dämpfungsverzerrungen auf. | + | - $y_3(t)$ weist gegenüber $x_3(t)$ Dämpfungsverzerrungen auf. |
| − | - $y_3(t)$ weist gegenüber $x_3(t)$ Phasenverzerrungen auf. | + | - $y_3(t)$ weist gegenüber $x_3(t)$ Phasenverzerrungen auf. |
| − | {Welche Aussagen treffen für das Ausgangssignal | + | {Welche Aussagen treffen für das Ausgangssignal $y_4(t)$ zu? |
| − | zu? | ||
|type="[]"} | |type="[]"} | ||
| − | - $y_4(t)$ ist gegenüber $x_4(t)$ unverzerrt. | + | - $y_4(t)$ ist gegenüber $x_4(t)$ unverzerrt. |
| − | + $y_4(t)$ weist gegenüber $x_4(t)$ Dämpfungsverzerrungen auf. | + | + $y_4(t)$ weist gegenüber $x_4(t)$ Dämpfungsverzerrungen auf. |
| − | - $y_4(t)$ | + | - $y_4(t)$ weist gegenüber $x_4(t)$ Phasenverzerrungen auf. |
| − | {Es gelte nun $T_1 = 1 \ \rm ms$ und $T_2 = 5 \ \rm ms$. Welche Veränderungen ergeben sich gegenüber den bisherigen Ergebnissen? | + | {Es gelte nun $T_1 = 1 \ \rm ms$ und $T_2 = 5 \ \rm ms$. Welche Veränderungen ergeben sich gegenüber den bisherigen Ergebnissen? |
|type="[]"} | |type="[]"} | ||
+ Die obigen Aussagen hinsichtlich Verzerrungen sind weiterhin gültig. | + Die obigen Aussagen hinsichtlich Verzerrungen sind weiterhin gültig. | ||
- Fundierte Aussagen sind erst nach einer Neuberechnung möglich. | - Fundierte Aussagen sind erst nach einer Neuberechnung möglich. | ||
| − | - Die Kombination $T_1 = 1 \ \rm ms$ und $T_2 = 5 \ \rm ms$ führt bei allen Signalen zu Verzerrungen. | + | - Die Kombination $T_1 = 1 \ \rm ms$ und $T_2 = 5 \ \rm ms$ führt bei allen Signalen zu Verzerrungen. |
| Zeile 110: | Zeile 110: | ||
+ x_1(t) \star \delta (t - T) = x_1(t) + x_1(t-T).$$ | + x_1(t) \star \delta (t - T) = x_1(t) + x_1(t-T).$$ | ||
| − | Somit ist $y_1(t)$ ein Rechteckimpuls der Höhe $1$ und der Breite $2T$. | + | *Somit ist $y_1(t)$ ein Rechteckimpuls der Höhe $1$ und der Breite $2T$. |
| − | Zum gleichen Ergebnis – aber zeitaufwändiger – kommt man durch die Berechnung im Spektralbereich: | + | *Zum gleichen Ergebnis – aber zeitaufwändiger – kommt man durch die Berechnung im Spektralbereich: |
:$$Y_1(f) = X_1(f) \cdot H(f) = T \cdot \frac {\sin(\pi f T)}{\pi f T}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \cdot | :$$Y_1(f) = X_1(f) \cdot H(f) = T \cdot \frac {\sin(\pi f T)}{\pi f T}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \cdot | ||
| − | \ | + | \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big].$$ |
| − | Die komplexen Exponentialfunktionen können mit dem [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Darstellung_nach_Betrag_und_Phase|Satz von Euler]] wie folgt umgewandelt werden: | + | *Die komplexen Exponentialfunktionen können mit dem [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Darstellung_nach_Betrag_und_Phase|Satz von Euler]] wie folgt umgewandelt werden: |
:$${\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} | :$${\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} | ||
| − | \ | + | \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} |
| − | \cdot \ | + | \cdot \big[ {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \cdot 2 \cos(\pi f T) .$$ |
| − | Somit kann für das Ausgangsspektrum geschrieben werden: | + | *Somit kann für das Ausgangsspektrum geschrieben werden: |
:$$Y_1(f) = Y_{11}(f) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} | :$$Y_1(f) = Y_{11}(f) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} | ||
, \; \; {\rm mit } \; \; | , \; \; {\rm mit } \; \; | ||
| Zeile 128: | Zeile 128: | ||
[[Datei:P_ID925__LZI_A_2_7_a.png|right|frame|Eingangs– und Ausgangssignale]] | [[Datei:P_ID925__LZI_A_2_7_a.png|right|frame|Eingangs– und Ausgangssignale]] | ||
| − | Hierbei ist die $t = 0$ symmetrischen Rechteck der Breite $2T$. Durch die Phasenfunktion wird dieser in den Bereich $0$ ... $2T$ verschoben und das Ergebnis der Zeitbereichsberechnung bestätigt. | + | Hierbei ist die Beziehung $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ verwendet. |
| + | |||
| + | *Die Fourierrücktransformation von $Y_{11}(f)$ führt zu einem um $t = 0$ symmetrischen Rechteck der Breite $2T$. | ||
| + | *Durch die Phasenfunktion wird dieser in den Bereich $0$ ... $2T$ verschoben und das Ergebnis der Zeitbereichsberechnung bestätigt. | ||
| + | |||
| + | |||
| + | Trotz der Tatsache, dass $y_1(t)$ ebenso wie $x_1(t)$ rechteckförmig ist, liegen Verzerrungen vor: | ||
| + | *Wegen $T_y > T_x$ sind diese linear. Im interessierenden Frequenzbereich $($das sind bei einem sinc–förmigem Spektrum alle Frequenzen$)$ ist $|H(f)|$ nicht konstant. Also gibt es Dämpfungsverzerrungen. | ||
| + | *Da zudem die Phase nicht im gesamten Bereich linear mit $f$ ansteigt, gibt es auch Phasenverzerrungen ⇒ Richtig sind die <u> Lösungsvorschläge 1, 3, 4 und 5</u>. | ||
| − | |||
| − | |||
| − | |||
| − | '''(2)''' Aufgrund der bereits in (1) angegebenen Gleichung | + | '''(2)''' Aufgrund der bereits in '''(1)''' angegebenen Gleichung |
:$$y_2(t) = x_2(t) + x_2(t-T)$$ | :$$y_2(t) = x_2(t) + x_2(t-T)$$ | ||
| − | erhält man einen stufenförmigen Verlauf entsprechend | + | erhält man einen stufenförmigen Verlauf entsprechend dem unteren Diagramm der obere Grafik. |
| − | |||
| − | |||
| + | Die gesuchten Zahlenwerte sind: $y_2(t = 0.5 T) \hspace{0.15cm}\underline{= 1}, \hspace{0.3cm} y_2(t = 1.5 T) \hspace{0.15cm}\underline{= 2}, | ||
| + | \hspace{0.3cm}y_2(t = 2.5 T) \hspace{0.15cm}\underline{ = 1}.$ | ||
| − | |||
| − | |||
| − | Die Spektralbereichsberechnung führt zum gleichen Ergebnis. $X_3(f)$ ist ein Linienspektrum mit Anteilen bei den Frequenzen $f = 0$, | + | [[Datei:P_ID927__LZI_A_2_7_c.png|right|frame|Lösungen '''(3)''' und '''(4)''']] |
| − | $f = \pm f_0 = \pm 1/T$, $f = \pm 3f_0$, usw.. Bei diesen diskreten Frequenzen gilt aber exakt: | + | '''(3)''' Die Periodendauer $T_0 = T$ des periodischen Signals $x_3(t)$ ist genau so groß wie die Verzögerung auf dem zweiten Pfad. Deshalb ist $y_3(t) = 2 \cdot x_3(t) $ und es sind keine Verzerrungen feststellbar. |
| + | |||
| + | Die Spektralbereichsberechnung führt zum gleichen Ergebnis. | ||
| + | *$X_3(f)$ ist ein Linienspektrum mit Anteilen bei den Frequenzen $f = 0$, $f = \pm f_0 = \pm 1/T$, $f = \pm 3f_0$, usw.. | ||
| + | *Bei diesen diskreten Frequenzen gilt aber exakt: | ||
:$$|H(f)| = 2, \hspace{0.3cm} b(f) = 0 \hspace{0.3cm} \Rightarrow | :$$|H(f)| = 2, \hspace{0.3cm} b(f) = 0 \hspace{0.3cm} \Rightarrow | ||
\hspace{0.3cm}\tau_{\rm P}(f) = 0.$$ | \hspace{0.3cm}\tau_{\rm P}(f) = 0.$$ | ||
| − | Auch daraus folgt wieder $y_3(t) = 2 \cdot x_3(t) $. Richtig ist somit nur der <u>Lösungsvorschlag 1</u>. | + | *Auch daraus folgt wieder $y_3(t) = 2 \cdot x_3(t) $. |
| + | *Richtig ist somit nur der <u>Lösungsvorschlag 1</u>. | ||
| − | '''(4)''' Aus der unteren Skizze der zweiten Grafik geht hervor, dass $y_4(t) = 1$ gegenüber $x_4(t)$ verzerrt ist. Dabei handelt es sich um Dämpfungsverzerrungen ⇒ <u>Lösungsvorschlag 2</u>, wie die folgende Überlegung zeigt. | + | |
| − | *Wegen $T_0 = 2T$ weist das Signal $x_4(t)$ die Grundfrequenz $f_0 = 1/(2T)$ auf. | + | |
| − | *Bei allen ungeraden Vielfachen von $f_0$ hat somit der Frequenzgang Nullstellen. | + | '''(4)''' Aus der unteren Skizze der zweiten Grafik geht hervor, dass $y_4(t) = 1$ gegenüber $x_4(t)$ verzerrt ist. Dabei handelt es sich um Dämpfungsverzerrungen ⇒ <u>Lösungsvorschlag 2</u>, wie die folgende Überlegung zeigt. |
| − | *Die einzige verbleibende Spektrallinie von $Y_4(f)$ liegt bei $f = 0$, wobei gilt: | + | *Wegen $T_0 = 2T$ weist das Signal $x_4(t)$ die Grundfrequenz $f_0 = 1/(2T)$ auf. |
| + | *Bei allen ungeraden Vielfachen von $f_0$ hat somit der Frequenzgang Nullstellen. | ||
| + | *Die einzige verbleibende Spektrallinie von $Y_4(f)$ liegt bei $f = 0$, wobei gilt: | ||
:$$Y_4(f) = 2 \cdot 0.5 \cdot \delta (f) = 1 \cdot \delta (f) | :$$Y_4(f) = 2 \cdot 0.5 \cdot \delta (f) = 1 \cdot \delta (f) | ||
\hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_4(t) = 1.$$ | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_4(t) = 1.$$ | ||
| − | '''(5)''' Der Frequenzgang lautet nun mit $T_1 = 1 \ \rm ms$, $T_2 = 5 \ \rm ms$ und $T = T_2 -T_1 = 4 \ \rm ms$: | + | |
| + | '''(5)''' Der Frequenzgang lautet nun mit $T_1 = 1 \ \rm ms$, $T_2 = 5 \ \rm ms$ und $T = T_2 -T_1 = 4 \ \rm ms$: | ||
:$$H(f) = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f | :$$H(f) = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f | ||
T_1}+ {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f | T_1}+ {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f | ||
| − | T_2}= \ | + | T_2}= \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} |
| − | \ | + | \big]\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f |
T_1}.$$ | T_1}.$$ | ||
| − | Der Klammerausdruck beschreibt den bereits bisher betrachteten Frequenzgang. Der zweite Term bewirkt eine zusätzliche Laufzeit um $ \tau = T_1$, und es gilt für alle Signale ( | + | *Der Klammerausdruck beschreibt den bereits bisher betrachteten Frequenzgang. |
| − | $$y_i^{\rm (5)}(t) = y_i(t-T_1).$$ | + | *Der zweite Term bewirkt eine zusätzliche Laufzeit um $ \tau = T_1$, und es gilt für alle Signale $(i = 1, 2, 3, 4)$: |
| + | :$$y_i^{\rm (5)}(t) = y_i(t-T_1).$$ | ||
| − | Alle Aussagen hinsichtlich der Verzerrungen sind weiter gültig. Dies entspricht dem <u>Lösungsvorschlag 1</u>. | + | Alle Aussagen hinsichtlich der Verzerrungen sind weiter gültig. Dies entspricht dem <u>Lösungsvorschlag 1</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 6. Oktober 2021, 16:18 Uhr
Wie in Aufgabe 2.6 wird ein Zweiwegekanal betrachtet, für dessen Impulsantwort gelte:
- $$h(t) = \delta ( t - T_1) + \delta ( t - T_2).$$
Entgegen der allgemeinen Darstellung in Aufgabe 2.6 sind hier die beiden Dämpfungsfaktoren gleich: $z_1 = z_2 = 1$.
- Dies entspricht zum Beispiel beim Mobilfunk einem Echo im Abstand $T_2 - T_1$ in gleicher Stärke wie das Signal auf dem Hauptpfad.
- Für dieses wird die Laufzeit $T_1$ vorausgesetzt.
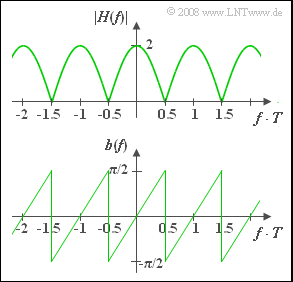
Mit den in den Teilaufgaben (1) ... (4) betrachteten Laufzeiten $T_1 = 0$ und $T_2 = T = 4 \ \rm ms$ erhält man für den Frequenzgang des Zweiwegekanals, dessen Betrag in der oberen Grafik dargestellt ist:
- $$H(f) = 1 + {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f T} = 1 + \cos(2 \pi f T) - {\rm j} \cdot \sin(2 \pi f T)$$
- $$\Rightarrow \hspace{0.4cm}|H(f)| = \sqrt{2\left(1 + \cos(2 \pi f T)\right)}= 2 \cdot |\cos(\pi f T)|.$$
Die untere Grafik zeigt die Phasenfunktion für $T_1 = 0$ und $T_2 = T = 4 \ \rm ms$:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) = \arctan \frac{\sin(2 \pi f T)}{1 + \cos(2 \pi f T)} = \arctan \big[\tan(\pi f T)\big].$$
- Im Frequenzbereich $|f| < 1/(2T)$ steigt $b(f)$ linear an: $b(f) = \pi \cdot f \cdot T.$
- Auch in den weiteren Abschnitten der Phasenfunktion nimmt die Phase stets von $-\pi/2$ bis $+\pi/2$ linear zu.
- Hierbei wurde folgende trigonometrische Umformung benutzt:
- $$ \frac{\sin(2 \alpha)}{1 + \cos(2 \alpha)} = \tan(\alpha).$$
Im Fragenkatalog bezeichnet $y_i(t)$ das Signal am Ausgang des Zweiwegekanals, wenn am Eingang das Signal $x_i(t)$ anliegt $( i = 1, 2, 3, 4)$.
Als Eingangssignale werden untersucht:
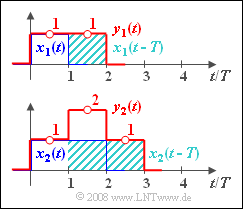
- ein Rechteckimpuls $x_1(t)$ mit Höhe $1$ zwischen $t= 0$ und $t= T$; für $t < 0$ und $t > T$ ist $x_1(t) = 0$ $($an den beiden Sprungstellen tritt jeweils der Wert $0.5$ auf$)$;
- ein Rechteckimpuls $x_2(t)$ mit Höhe $1$ im Bereich von $0 \ \text{...} \ 2T$;
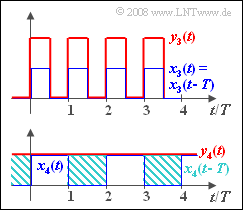
- ein periodisches Rechtecksignal $x_3(t)$ mit der Periodendauer $T = T_0$:
- $$x_3(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} { 0 < t < T/2,} \\ { T/2 < t < T,} \\ \end{array}$$
- ein periodisches Rechtecksignal $x_4(t)$ mit der Periodendauer $T = 2T_0$:
- $$x_4(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} { 0 < t < T,} \\ { T < t < 2T.} \\ \end{array}$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Lineare Verzerrungen.
- Für die Teilaufgaben (1) bis (4) gelte $T_1 = 0$ und $T_2 = T = 4 \ \rm ms$.
- In Teilaufgabe (5) wird der Fall $T_1 = 1 \ \rm ms$ und $T_2 = 5 \ \rm ms$ betrachtet.
Fragebogen
Musterlösung
- $$y_1(t) = x_1(t) \star h(t) = x_1(t) \star \delta (t) + x_1(t) \star \delta (t - T) = x_1(t) + x_1(t-T).$$
- Somit ist $y_1(t)$ ein Rechteckimpuls der Höhe $1$ und der Breite $2T$.
- Zum gleichen Ergebnis – aber zeitaufwändiger – kommt man durch die Berechnung im Spektralbereich:
- $$Y_1(f) = X_1(f) \cdot H(f) = T \cdot \frac {\sin(\pi f T)}{\pi f T}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \cdot \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big].$$
- Die komplexen Exponentialfunktionen können mit dem Satz von Euler wie folgt umgewandelt werden:
- $${\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \cdot \big[ {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \cdot 2 \cos(\pi f T) .$$
- Somit kann für das Ausgangsspektrum geschrieben werden:
- $$Y_1(f) = Y_{11}(f) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} , \; \; {\rm mit } \; \; Y_{11}(f) = 2T \cdot \frac {\sin(\pi f T) \cdot \cos(\pi f T)}{\pi f T} = 2T \cdot \frac {\sin(2\pi f T) }{2\pi f T}.$$
Hierbei ist die Beziehung $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ verwendet.
- Die Fourierrücktransformation von $Y_{11}(f)$ führt zu einem um $t = 0$ symmetrischen Rechteck der Breite $2T$.
- Durch die Phasenfunktion wird dieser in den Bereich $0$ ... $2T$ verschoben und das Ergebnis der Zeitbereichsberechnung bestätigt.
Trotz der Tatsache, dass $y_1(t)$ ebenso wie $x_1(t)$ rechteckförmig ist, liegen Verzerrungen vor:
- Wegen $T_y > T_x$ sind diese linear. Im interessierenden Frequenzbereich $($das sind bei einem sinc–förmigem Spektrum alle Frequenzen$)$ ist $|H(f)|$ nicht konstant. Also gibt es Dämpfungsverzerrungen.
- Da zudem die Phase nicht im gesamten Bereich linear mit $f$ ansteigt, gibt es auch Phasenverzerrungen ⇒ Richtig sind die Lösungsvorschläge 1, 3, 4 und 5.
(2) Aufgrund der bereits in (1) angegebenen Gleichung
- $$y_2(t) = x_2(t) + x_2(t-T)$$
erhält man einen stufenförmigen Verlauf entsprechend dem unteren Diagramm der obere Grafik.
Die gesuchten Zahlenwerte sind: $y_2(t = 0.5 T) \hspace{0.15cm}\underline{= 1}, \hspace{0.3cm} y_2(t = 1.5 T) \hspace{0.15cm}\underline{= 2}, \hspace{0.3cm}y_2(t = 2.5 T) \hspace{0.15cm}\underline{ = 1}.$
(3) Die Periodendauer $T_0 = T$ des periodischen Signals $x_3(t)$ ist genau so groß wie die Verzögerung auf dem zweiten Pfad. Deshalb ist $y_3(t) = 2 \cdot x_3(t) $ und es sind keine Verzerrungen feststellbar.
Die Spektralbereichsberechnung führt zum gleichen Ergebnis.
- $X_3(f)$ ist ein Linienspektrum mit Anteilen bei den Frequenzen $f = 0$, $f = \pm f_0 = \pm 1/T$, $f = \pm 3f_0$, usw..
- Bei diesen diskreten Frequenzen gilt aber exakt:
- $$|H(f)| = 2, \hspace{0.3cm} b(f) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\tau_{\rm P}(f) = 0.$$
- Auch daraus folgt wieder $y_3(t) = 2 \cdot x_3(t) $.
- Richtig ist somit nur der Lösungsvorschlag 1.
(4) Aus der unteren Skizze der zweiten Grafik geht hervor, dass $y_4(t) = 1$ gegenüber $x_4(t)$ verzerrt ist. Dabei handelt es sich um Dämpfungsverzerrungen ⇒ Lösungsvorschlag 2, wie die folgende Überlegung zeigt.
- Wegen $T_0 = 2T$ weist das Signal $x_4(t)$ die Grundfrequenz $f_0 = 1/(2T)$ auf.
- Bei allen ungeraden Vielfachen von $f_0$ hat somit der Frequenzgang Nullstellen.
- Die einzige verbleibende Spektrallinie von $Y_4(f)$ liegt bei $f = 0$, wobei gilt:
- $$Y_4(f) = 2 \cdot 0.5 \cdot \delta (f) = 1 \cdot \delta (f) \hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_4(t) = 1.$$
(5) Der Frequenzgang lautet nun mit $T_1 = 1 \ \rm ms$, $T_2 = 5 \ \rm ms$ und $T = T_2 -T_1 = 4 \ \rm ms$:
- $$H(f) = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}+ {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2}= \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big]\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}.$$
- Der Klammerausdruck beschreibt den bereits bisher betrachteten Frequenzgang.
- Der zweite Term bewirkt eine zusätzliche Laufzeit um $ \tau = T_1$, und es gilt für alle Signale $(i = 1, 2, 3, 4)$:
- $$y_i^{\rm (5)}(t) = y_i(t-T_1).$$
Alle Aussagen hinsichtlich der Verzerrungen sind weiter gültig. Dies entspricht dem Lösungsvorschlag 1.