Aufgabe 2.7: Ist der Modulationsgrad zu groß?
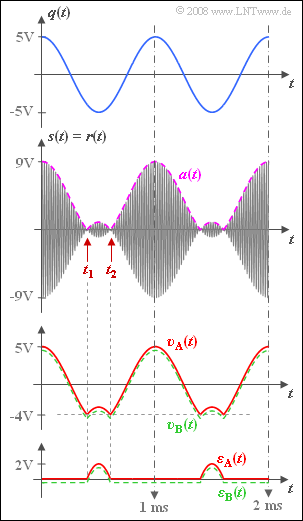
Das cosinusförmige Quellensignal $q(t)$ mit Amplitude $A_N = 5 V$ und Frequenz $f_N = 1 kHz$ wird (ZSB–) amplitudenmoduliert. Für das Empfangssignal gilt bei idealem Kanal: $$r(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (2\pi \cdot f_{\rm T}\cdot t )\hspace{0.05cm}.$$ Es handelt sich also um die „ZSB–AM mit Träger”.
In der Grafik sind neben dem Quellensignal $q(t)$ und dem Empfangssignal $r(t)$ inklusive dessen Hüllkurve $a(t)$ auch das Sinkensignal $υ(t)$ und das Fehlersignal $$ \varepsilon(t) = v(t) - q(t)$$ dargestellt. Das rot gezeichnete Sinkensignal $$v_{\rm A}(t) = a(t) - A_{\rm T}$$ gehört zu einem Hüllkurvendemodulator, bei dem von der Hüllkurve $a(t)$ genau der beim Sender zugeführte Träger ($A_T$) subtrahiert wird. Dieses Signal $υ_A(t)$ besitzt ebenso wie das zugehörige Fehlersignal $ε_A(t)$ einen Gleichanteil. Aufgrund der Periodizität kann es durch die folgende Fourierreihe approximiert werden: $$v_{\rm A}(t) = A_0 + \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),$$ $${\rm mit}\hspace{0.3cm}A_0 = 0.272\,{\rm V},\hspace{0.3cm}A_1 = 4.480\,{\rm V},\hspace{0.3cm}A_2 = 0.458\,{\rm V},\hspace{0.3cm}A_3 = -0.367\,{\rm V},\hspace{0.3cm}$$ $$A_4 = 0.260\,{\rm V},\hspace{0.3cm}A_5 = -0.155\,{\rm V},\hspace{0.3cm}A_6 = 0.066\,{\rm V}\hspace{0.05cm}.$$ Wird dagegen der Gleichanteil von a(t) durch einen idealen Hochpass eliminiert, so ergeben sich die gleichsignalfreien Signale $$ v_{\rm B}(t) = \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),\hspace{0.5cm}\varepsilon_{\rm B}(t) = v_{\rm B}(t) - q(t) = a(t) - A_{\rm T} - A_0 \hspace{0.05cm}.$$
Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 1.2 und das Kapitel 2.3 dieses Buches sowie auf das Kapitel 2.2 im Buch „Lineare zeitinvariante Systeme”.
Zur Lösung dieser Aufgabe sind folgende unbestimmte Integrale gegeben: $$ \int { \cos (a x )}\hspace{0.1cm}{\rm d}x =\frac{1}{a} \cdot \sin (a x ), \hspace{0.5cm} \int { \cos^2 (a x )}\hspace{0.1cm}{\rm d}x = \frac{x}{2} +\frac{1}{4a} \cdot \sin (2a x ).$$ Die Klirrfaktoren berechnen sich entsprechend $$K_2 = {A_2}/{A_1}, \hspace{0.3cm} K_3 = {A_3}/{A_1}, \hspace{0.1cm} ... \hspace{0.5cm} \Rightarrow \hspace{0.5cm}K = \sqrt{K_2^2 +K_3^2 + ...}\hspace{0.1cm} .$$
Fragebogen
Musterlösung
2. Aus der Bedingung $a(t) = q(t) + A_T = 0$ folgt direkt für die erste Nullstelle:
$$ \cos (2\pi \cdot f_{\rm N}\cdot t_1 ) = \frac{-A_{\rm T}}{A_{\rm N}}= -0.8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1 = \frac[[:Vorlage:\rm arccos(-0.8)]]{2\pi \cdot f_{\rm N}}\approx \frac[[:Vorlage:0.795 \cdot \pi]]{2\pi \cdot f_{\rm N}} \hspace{0.05cm}.$$
Mit $f_N = 1 kHz$ ergibt sich daraus $t_1 ≈ 0.4 ms$. Die zweite Nullstelle kann entsprechend zu $t_2 ≈ 0.6 ms$ berechnet werden.
3.Der Klirrfaktor zweiter Ordnung ist $K_2 = 0.458/4.48 ≈ 0.102$. Entsprechend gilt für den Klirrfaktor dritter Ordnung: $K_3 = 0.367/4.48 ≈ 0.082$. Die weiteren Klirrfaktoren sind $K_4 ≈ 0.058$, $K_5 ≈ 0.035$ sowie $K_6 ≈ 0.015$. Damit erhält man für den Gesamtklirrfaktor:
$$ K = \sqrt{K_2^2 + K_3^2 + K_4^2 + K_5^2 + K_6^2 }\hspace{0.15cm}\underline { \approx 14.8 \%}.$$
4.Die Verzerrungsleistung ergibt sich aus Mittelung von $ε_A(t)^2$ über eine Periodendauer $T_0 = 1 ms$:
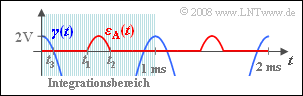
$$P_{\varepsilon \rm A} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{t_1}^{\hspace{0.1cm} t_2} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{I_{\varepsilon}}{T_{\rm 0}}\hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass das Fehlersignal $ε_A(t)$ außerhalb des Intervalls von $t_1$ und $t_2$ gleich 0 ist.
Wie aus der Skizze hervorgeht, ist $I_ε$ doppelt so groß als das Integral $I_γ$ der Hilfsgröße $γ$ im Intervall von 0 bis $t_3 = (t_2 – t_1)/2 ≈ 0.1 ms$:
$$I_{\gamma} = \int_{0}^{\hspace{0.1cm} t_3} {\gamma^2(t) }\hspace{0.1cm}{\rm d}t = \hspace{0.3cm}{\rm mit}\hspace{0.3cm} \gamma(t) = 2 \cdot \left( A_{\rm N} \cdot \cos (\omega_{\rm N}\cdot t ) - A_{\rm T}\right)\hspace{0.05cm}.$$ Eine Nebenrechnung liefert: $$: I_{\gamma} = 4 \cdot \left( I_1 + I_2 + I_3 \right)\hspace{0.3cm}{\rm mit}$$ $$I_1 = A_{\rm N}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {\cos^2 (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = A_{\rm N}^2 \cdot \left[ \frac{t_3}{2} + \frac{\sin (2 \omega_{\rm N}\cdot t_3 )}{4 \omega_{\rm N}} \right] =$$ $$ = 25\,{\rm V}^2 \cdot \left[ 0.05\,{\rm ms} + 0.0378\,{\rm ms} \right] = 2.196 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$ $$ I_2 = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \int_{0}^{\hspace{0.1cm} t_3} {\cos (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \frac{\sin (\omega_{\rm N}\cdot t_3 )}{\omega_{\rm N}} =$$ $$ = - 2 \cdot 5\,{\rm V} \cdot 4\,{\rm V}\cdot 0.0935\,{\rm ms} = -3.742 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$ $$ I_3 = A_{\rm T}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {}\hspace{0.1cm}{\rm d}t = A_{\rm T}^2 \cdot {t_3} = 1.6 \cdot 10^{-3}\,{\rm V^2 s}$$ $$\Rightarrow \hspace{0.3cm}I_{\gamma} = 0.216 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}I_{\varepsilon} = 2 \cdot I_{\gamma} =0.432 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm}.$$ Somit erhält man als Endergebnis: $$P_{\varepsilon \rm A} = \frac{I_{\varepsilon}}{T_{\rm 0}}\hspace{0.15cm}\underline {=0.432 \,{\rm V^2 }}\hspace{0.05cm}.$$
5.Die beiden Sinkensignale $υ_A(t)$ und $υ_B(t)$ unterscheiden sich ebenso wie die beiden Fehlersignale $ε_A(t)$ und $ε_B(t)$ um den Gleichanteil $A_0$. Deshalb gilt: $$ P_{\varepsilon \rm B} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm B}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\left[\varepsilon_{\rm A}(t) - A_0 \right]^2}\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ Hierfür kann auch geschrieben werden: $$P_{1} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = P_{\varepsilon \rm A} \hspace{0.05cm},$$ $$P_{2} = - 2 A_0 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}(t) }\hspace{0.1cm}{\rm d}t = - 2 A_0^2 \hspace{0.05cm},$$ $$P_{3} = A_0^2 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} { }\hspace{0.1cm}{\rm d}t = A_0^2 \hspace{0.05cm}.$$ Damit ergibt sich für den quadratischen Mittelwert des Fehlersignals $ε_B(t)$: $$P_{\varepsilon \rm B} = P_{\varepsilon \rm A}- A_0^2 = 0.432\,{\rm V}^2 - (0.272\,{\rm V})^2 \hspace{0.15cm}\underline {= 0.358\,{\rm V}^2} \hspace{0.05cm}.$$ Ein ähnliches Ergebnis hätte man auch nach folgendem Rechengang erhalten: $$ P_{\varepsilon \rm B} = \frac{1\,{\rm V}^2}{2} \cdot \left[ (5 - 4.48)^2 + 0.458^2 + 0.367^2 + ... + 0.066^2 \right] \approx 0.356\,{\rm V}^2 \hspace{0.05cm}.$$ Der geringe Unterschied in beiden Rechengängen ist darauf zurückzuführen, dass die Fourierkoeffizienten $A_7, A_8$, .... zwar sehr klein, aber nicht identisch 0 sind.
6. Die Leistung des Quellensignals $q(t)$ beträgt $P_q = A_N²/2 = 12.5 V²$. Daraus ergeben sich die beiden S/N–Verhältnisse:
$$\rho_{v {\rm A}} = \frac{P_{q}}{P_{\varepsilon \rm A}} \hspace{0.15cm}\underline {= 28.94} \hspace{0.05cm}, \hspace{0.3cm} \rho_{v {\rm B}} = \frac{P_{q}}{P_{\varepsilon \rm B}}\hspace{0.15cm}\underline { = 34.92} \hspace{0.05cm}.$$
Dies zeigt, dass der HKD mit Hochpass um etwa 6 dB besser ist als der Demodulator A.
Anzumerken ist, dass die Näherung $ρ_υ = α_2 · P_q/K^2$ hier zum verfälschten Zahlenwert $ρ_υ = 36.66$ führen würde. Dieses unterschiedliche Ergebnis wird auf der Seite Klirrfaktor (2) im Kapitel 2.2 des Buches „Lineare zeitinvariante Systeme” ausführlich begründet, wobei genau die für diese Aufgabe getroffenen Voraussetzungen zugrunde gelegt sind.