Aufgaben:Aufgabe 2.7: AMI-Code: Unterschied zwischen den Versionen
| Zeile 70: | Zeile 70: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Die Modulo–2–Addition kann auch als Antivalenz aufgefasst werden. Es gilt $b_{\nu} = +1$, falls sich $q_{\nu}$ und $b_{\nu – 1}$ unterscheiden, andernfalls ist $b_{\nu} = -1$ zu setzen. Mit dem Startwert $b_{0} = –1$ erhält man: |
| − | '''(2)''' | + | :$$b_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} b_2 = +1, \hspace{0.2cm}b_3 = -1, \hspace{0.2cm}b_4 = +1, \hspace{0.2cm}b_5 = +1, \hspace{0.2cm}b_6 = -1\hspace{0.05cm},$$ |
| + | :$$b_7 = +1, \hspace{0.2cm} b_8 = +1, \hspace{0.2cm}b_9 = +1, \hspace{0.2cm}b_{10} = +1, \hspace{0.2cm}b_{11} \hspace{0.15cm}\underline {= +1}, \hspace{0.2cm}b_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(2)''' Die AMI–Codierung liefert die folgenden Amplitudenkoeffizienten: | ||
| + | :$$a_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} a_2 = 0, \hspace{0.2cm}a_3 = -1, \hspace{0.2cm}a_4 = +1, \hspace{0.2cm}a_5 = 0, \hspace{0.2cm}a_6 = -1\hspace{0.05cm},$$ | ||
| + | :$$a_7 = +1, \hspace{0.2cm} a_8 = 0, \hspace{0.2cm}a_9 = 0, \hspace{0.2cm}a_{10} = 0, \hspace{0.2cm}a_{11}\hspace{0.15cm}\underline { = 0}, \hspace{0.2cm}a_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$ | ||
| + | Zu diesem Ergebnis kommt man entweder über die Gleichung $a_{\nu} = (b_{\nu} – b_{\nu –1})/2$ oder durch direkte Anwendung der einfachen AMI–Codierregel: | ||
| + | *Ein Quellensymbol $q_{\nu} = –1$ führt stets zu $a_{\nu} = 0$. | ||
| + | *Die Quellensymbole $q_{\nu} = +1$ führen alternierend zu $a_{\nu} = +1$ und $a_{\nu} = –1$. | ||
| + | |||
'''(3)''' | '''(3)''' | ||
'''(4)''' | '''(4)''' | ||
Version vom 13. November 2017, 14:34 Uhr
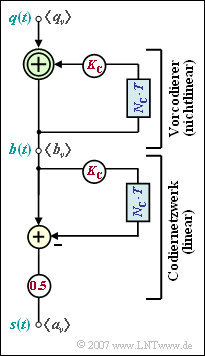
Die Grafik zeigt das Blockschaltbild zur AMI–Codierung, wobei von den binären bipolaren Amplitudenkoeffizienten $q_{\nu} ∈ \{–1, +1\}$ am Eingang ausgegangen wird. Diese Umcodierung erfolgt zweistufig:
- Im ersten Teil des Blockschaltbildes wird bei jedem Taktschritt ein binär–vorcodiertes Symbol $b_{\nu}$ aus der Modulo–2–Addition von $q_{\nu}$ und $b_{\nu -1}$ erzeugt. Es gilt $b_{\nu} ∈ \{–1, +1\}.$
- Danach wird durch eine herkömmliche Subtraktion der aktuelle Amplitudenkoeffizient des ternären Sendesignals $s(t)$ bestimmt. Dabei gilt:
- $$a_\nu = {1}/{2} \cdot \left [ b_\nu - b_{\nu-1} \right ] \hspace{0.05cm}.$$
Aufgrund der AMI–Codierung wird sichergestellt, dass keine langen „$+1$”– bzw. „$–1$”–Sequenzen entstehen. Um auch lange Nullfolgen zu vermeiden, wurden auch modifizierte AMI–Codes entwickelt:
- Beim HDB3–Code werden je vier aufeinanderfolgende Nullen durch eine gezielte Verletzung der AMI–Codierregel markiert.
- Beim B6ZS–Code werden sechs aufeinanderfolgende Nullen durch eine gezielte Verletzung der AMI–Codierregel markiert.
Das Leistungsdichtespektrum ${\it \Phi}_{a}(f)$ der Amplitudenkoeffizienten soll aus den diskreten AKF–Werten $\varphi_{a}(\lambda) = {\E}[a_{\nu} \cdot a_{\nu + \lambda}]$ ermittelt werden. Die Fouriertransformation lautet in dieser diskreten Darstellung:
- $${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$
Hinweis:
Die Aufgabe bezieht sich auf Symbolweise Codierung mit Pseudoternärcodes. Sie können Ihre Ergebnisse mit folgendem Interaktionsmodul überprüfen: Signale, AKF und LDS der Pseutoternärcodes
Fragebogen
Musterlösung
- $$b_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} b_2 = +1, \hspace{0.2cm}b_3 = -1, \hspace{0.2cm}b_4 = +1, \hspace{0.2cm}b_5 = +1, \hspace{0.2cm}b_6 = -1\hspace{0.05cm},$$
- $$b_7 = +1, \hspace{0.2cm} b_8 = +1, \hspace{0.2cm}b_9 = +1, \hspace{0.2cm}b_{10} = +1, \hspace{0.2cm}b_{11} \hspace{0.15cm}\underline {= +1}, \hspace{0.2cm}b_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$
(2) Die AMI–Codierung liefert die folgenden Amplitudenkoeffizienten:
- $$a_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} a_2 = 0, \hspace{0.2cm}a_3 = -1, \hspace{0.2cm}a_4 = +1, \hspace{0.2cm}a_5 = 0, \hspace{0.2cm}a_6 = -1\hspace{0.05cm},$$
- $$a_7 = +1, \hspace{0.2cm} a_8 = 0, \hspace{0.2cm}a_9 = 0, \hspace{0.2cm}a_{10} = 0, \hspace{0.2cm}a_{11}\hspace{0.15cm}\underline { = 0}, \hspace{0.2cm}a_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$
Zu diesem Ergebnis kommt man entweder über die Gleichung $a_{\nu} = (b_{\nu} – b_{\nu –1})/2$ oder durch direkte Anwendung der einfachen AMI–Codierregel:
- Ein Quellensymbol $q_{\nu} = –1$ führt stets zu $a_{\nu} = 0$.
- Die Quellensymbole $q_{\nu} = +1$ führen alternierend zu $a_{\nu} = +1$ und $a_{\nu} = –1$.
(3) (4) (5) (6)