Aufgaben:Aufgabe 2.6: GF(P hoch m). Welches P, welches m?: Unterschied zwischen den Versionen
K (Textersetzung - „* Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Erweiterungskörper}} | {{quiz-Header|Buchseite=Kanalcodierung/Erweiterungskörper}} | ||
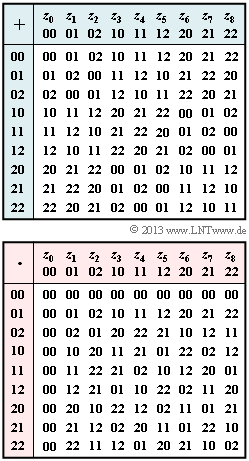
| − | [[Datei:P_ID2510__KC_A_2_6_neu.png|right|frame|Zugrunde liegende Tabellen für | + | [[Datei:P_ID2510__KC_A_2_6_neu.png|right|frame|Zugrunde liegende Tabellen für Addition und Multiplikation]] |
| − | Es soll ein Galoisfeld ${\rm GF}(q)$ mit $q = P^m$ Elementen analysiert werden, das durch die nebenstehenden Tabellen definiert ist | + | Es soll ein Galoisfeld ${\rm GF}(q)$ mit $q = P^m$ Elementen analysiert werden, das durch die nebenstehenden Tabellen definiert ist |
| − | *für Addition (gekennzeichnet mit „$+$”) und | + | *für Addition (gekennzeichnet mit „$+$”), und |
| − | *für Multiplikation (gekennzeichnet mit „$\cdot$”). | + | *für Multiplikation (gekennzeichnet mit „$\hspace{0.05cm}\cdot\hspace{0.05cm}$”). |
| − | Dieses Galoisfeld ${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.05cm} \text{...} , \hspace{0.1cm}z_{q-1}\}$ erfüllt alle Anforderungen an einen endlichen Körper, die im Kapitel [[Kanalcodierung/Einige_Grundlagen_der_Algebra|Einige Grundlagen der Algebra]] aufgeführt sind. Kommutativ–, Assoziativ– und Distributivgesetz | + | Dieses Galoisfeld ${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.05cm} \text{...} , \hspace{0.1cm}z_{q-1}\}$ erfüllt alle Anforderungen an einen endlichen Körper, die im Kapitel [[Kanalcodierung/Einige_Grundlagen_der_Algebra|Einige Grundlagen der Algebra]] aufgeführt sind. So werden auch Kommutativ–, Assoziativ– und Distributivgesetz erfüllt. |
| + | |||
| + | Weiterhin gibt es | ||
* ein neutrales Element hinsichtlich Addition ⇒ $N_{\rm A}$: | * ein neutrales Element hinsichtlich Addition ⇒ $N_{\rm A}$: | ||
:$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} | :$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} | ||
| − | \hspace{0.25cm}z_i + z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm A} | + | \hspace{0.25cm}z_i + z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm A} \hspace{0.25cm}{\rm (Nullelement)} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
* ein neutrales Element hinsichtlich Multiplikation ⇒ $N_{\rm M}$: | * ein neutrales Element hinsichtlich Multiplikation ⇒ $N_{\rm M}$: | ||
:$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} | :$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} | ||
| − | \hspace{0.25cm}z_i \cdot z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm M} | + | \hspace{0.25cm}z_i \cdot z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm M} \hspace{0.25cm}{\rm (Einselement)} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * für alle Elemente $z_i$ eine additive Inverse ⇒ ${\rm Inv_A}(z_i)$: | + | * für alle Elemente $z_i$ eine additive Inverse ⇒ ${\rm Inv_A}(z_i)$: |
:$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q)\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}$$ | :$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q)\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}$$ | ||
::$$z_i + {\rm Inv_A}(z_i) = N_{\rm A} = {\rm "0"}\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm kurz}\text{:}\hspace{0.15cm} | ::$$z_i + {\rm Inv_A}(z_i) = N_{\rm A} = {\rm "0"}\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm kurz}\text{:}\hspace{0.15cm} | ||
{\rm Inv_A}(z_i) = - z_i \hspace{0.05cm}, $$ | {\rm Inv_A}(z_i) = - z_i \hspace{0.05cm}, $$ | ||
| − | * für alle Elemente $z_i$ mit Ausnahme des Nullelements eine multiplikative Inverse ⇒ ${\rm Inv_M}(z_i)$: | + | * für alle Elemente $z_i$ mit Ausnahme des Nullelements eine multiplikative Inverse ⇒ ${\rm Inv_M}(z_i)$: |
:$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne N_{\rm A} \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}$$ | :$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne N_{\rm A} \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}$$ | ||
::$$z_i \cdot {\rm Inv_M}(z_i) = N_{\rm M} = {\rm "1"} | ::$$z_i \cdot {\rm Inv_M}(z_i) = N_{\rm M} = {\rm "1"} | ||
| Zeile 26: | Zeile 28: | ||
{\rm Inv_M}(z_i) = z_i^{-1} | {\rm Inv_M}(z_i) = z_i^{-1} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| Zeile 31: | Zeile 37: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Erweiterungsk%C3%B6rper| Erweiterungskörper]]. | + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Erweiterungsk%C3%B6rper| Erweiterungskörper]]. |
| − | * In den Tabellen sind die Elemente $z_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \ z_8$ als Koeffizientenvektoren bezeichnet. Zum Beispiel steht „$ | + | * In den Tabellen sind die Elemente $z_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \ z_8$ als Koeffizientenvektoren bezeichnet. Zum Beispiel steht „$2\hspace{0.03cm}1$” für „$2 \cdot \alpha + 1$”. |
| Zeile 48: | Zeile 54: | ||
{Wie lautet das neutrale Element für die Addition? | {Wie lautet das neutrale Element für die Addition? | ||
|type="()"} | |type="()"} | ||
| − | + Das neutrale Element der Addition ist $N_{\rm A} = \,$ „$ | + | + Das neutrale Element der Addition ist $N_{\rm A} = \,$ „$0\hspace{0.03cm}0$”, |
| − | - Das neutrale Element der Addition ist $N_{\rm A} = \,$ „$ | + | - Das neutrale Element der Addition ist $N_{\rm A} = \,$ „$0\hspace{0.03cm}1$”. |
{Wie lautet das neutrale Element für die Multiplikation? | {Wie lautet das neutrale Element für die Multiplikation? | ||
|type="()"} | |type="()"} | ||
| − | - Das neutrale Element der Multiplikation ist $N_{\rm M} = \,$ „$ | + | - Das neutrale Element der Multiplikation ist $N_{\rm M} = \,$ „$0\hspace{0.03cm}0$”, |
| − | + Das neutrale Element der Multiplikation ist $N_{\rm M} = \,$ „$ | + | + Das neutrale Element der Multiplikation ist $N_{\rm M} = \,$ „$0\hspace{0.03cm}1$”. |
{Welche Aussagen gelten hinsichtlich der additiven Inversen? | {Welche Aussagen gelten hinsichtlich der additiven Inversen? | ||
|type="[]"} | |type="[]"} | ||
| − | + Es gilt ${\rm Inv_A} ($„$ | + | + Es gilt ${\rm Inv_A} ($„$0\hspace{0.03cm}2$”) $\, = \, $ „$0\hspace{0.03cm}1$”, |
| − | + Es gilt ${\rm Inv_A} ($„$ | + | + Es gilt ${\rm Inv_A} ($„$1\hspace{0.03cm}1$”) $\, = \, $ „$2\hspace{0.03cm}2$”, |
| − | - Es gilt ${\rm Inv_A} ($„$ | + | - Es gilt ${\rm Inv_A} ($„$2\hspace{0.03cm}2$”) $\, = \, $ „$0\hspace{0.03cm}0$”. |
{Welche der folgenden Aussagen treffen für die Multiplikation zu? | {Welche der folgenden Aussagen treffen für die Multiplikation zu? | ||
|type="[]"} | |type="[]"} | ||
| − | - Die Multiplikation erfolgt modulo $p(\alpha) = \alpha^2 + 2$. | + | - Die Multiplikation erfolgt modulo $p(\alpha) = \alpha^2 + 2$. |
| − | + Die Multiplikation erfolgt modulo $p(\alpha) = \alpha^2 + 2\alpha + 2$. | + | + Die Multiplikation erfolgt modulo $p(\alpha) = \alpha^2 + 2\alpha + 2$. |
{Welche Aussagen gelten hinsichtlich der multiplikativen Inversen? | {Welche Aussagen gelten hinsichtlich der multiplikativen Inversen? | ||
|type="[]"} | |type="[]"} | ||
| − | - Es gibt für alle Elemente $z_i ∈ {\rm GF}(P^m)$ eine multiplikative Inverse. | + | - Es gibt für alle Elemente $z_i ∈ {\rm GF}(P^m)$ eine multiplikative Inverse. |
| − | + Es gilt ${\rm Inv_M} ($„$ | + | + Es gilt ${\rm Inv_M} ($„$1\hspace{0.03cm}2$”) $\, = \, $ „$1\hspace{0.03cm}0$”. |
| − | - Es gilt ${\rm Inv_A} ($„$ | + | - Es gilt ${\rm Inv_A} ($„$2\hspace{0.03cm}1$”) $\, = \, $ „$1\hspace{0.03cm}2$”. |
| − | {Gilt („$ | + | {Gilt („$2\hspace{0.03cm}0$” $\, + \,$ „$1\hspace{0.03cm}2$”) $\, \cdot\, $ „$1\hspace{0.03cm}2$” $\, = \, $„$2\hspace{0.03cm}0$” $\, \cdot\, $ „$1\hspace{0.03cm}2$” $\, + \, $„$1\hspace{0.03cm}2$” $\, \cdot\, $ „$1\hspace{0.03cm}2$”? |
|type="()"} | |type="()"} | ||
+ Ja. | + Ja. | ||
Version vom 20. Mai 2019, 17:47 Uhr
Es soll ein Galoisfeld ${\rm GF}(q)$ mit $q = P^m$ Elementen analysiert werden, das durch die nebenstehenden Tabellen definiert ist
- für Addition (gekennzeichnet mit „$+$”), und
- für Multiplikation (gekennzeichnet mit „$\hspace{0.05cm}\cdot\hspace{0.05cm}$”).
Dieses Galoisfeld ${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.05cm} \text{...} , \hspace{0.1cm}z_{q-1}\}$ erfüllt alle Anforderungen an einen endlichen Körper, die im Kapitel Einige Grundlagen der Algebra aufgeführt sind. So werden auch Kommutativ–, Assoziativ– und Distributivgesetz erfüllt.
Weiterhin gibt es
- ein neutrales Element hinsichtlich Addition ⇒ $N_{\rm A}$:
- $$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i + z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm A} \hspace{0.25cm}{\rm (Nullelement)} \hspace{0.05cm},$$
- ein neutrales Element hinsichtlich Multiplikation ⇒ $N_{\rm M}$:
- $$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i \cdot z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm M} \hspace{0.25cm}{\rm (Einselement)} \hspace{0.05cm},$$
- für alle Elemente $z_i$ eine additive Inverse ⇒ ${\rm Inv_A}(z_i)$:
- $$\forall \hspace{0.15cm} z_i \in {\rm GF}(q)\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}$$
- $$z_i + {\rm Inv_A}(z_i) = N_{\rm A} = {\rm "0"}\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm kurz}\text{:}\hspace{0.15cm} {\rm Inv_A}(z_i) = - z_i \hspace{0.05cm}, $$
- für alle Elemente $z_i$ mit Ausnahme des Nullelements eine multiplikative Inverse ⇒ ${\rm Inv_M}(z_i)$:
- $$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne N_{\rm A} \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}$$
- $$z_i \cdot {\rm Inv_M}(z_i) = N_{\rm M} = {\rm "1"} \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm kurz}\text{:}\hspace{0.15cm} {\rm Inv_M}(z_i) = z_i^{-1} \hspace{0.05cm}. $$
Hinweise:
- Die Aufgabe gehört zum Kapitel Erweiterungskörper.
- In den Tabellen sind die Elemente $z_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \ z_8$ als Koeffizientenvektoren bezeichnet. Zum Beispiel steht „$2\hspace{0.03cm}1$” für „$2 \cdot \alpha + 1$”.
Fragebogen
Musterlösung
(2) Richtig ist der Lösungsvorschlag 1:
- Das neutrale Element der Addition $(N_{\rm A})$ erfüllt für alle $z_i ∈ {\rm GF}(P^m)$ die Bedingung $z_i + N_{\rm A} = z_i$.
- Aus der Additionstabelle kann abgelesen werden, dass „$00$” diese Bedingung erfült.
(3) Richtig ist der Lösungsvorschlag 2:
- Das neutrale Element der Multiplikation $(N_{\rm M})$ muss stets die Bedingung $z_i \cdot N_{\rm M} = z_i$ erfüllen.
- Aus der Multiplikationstabelle ergibt sich $N_{\rm M} = \, „01”$.
- In der Polynomschreibweise entspricht dies mit $k_1 = 0$ und $k_0 = 1$:
- $$k_1 \cdot \alpha + k_0 = 1 \hspace{0.05cm}.$$
(4) Mit der Polynomdarstellung ergeben sich folgende Berechnungen:
- $${\rm Inv_A}("02") \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(2) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = 1 \hspace{0.25cm}\Rightarrow \hspace{0.25cm}{\rm Vektor}\hspace{0.15cm}"01"\hspace{0.05cm},$$
- $${\rm Inv_A}("11") \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(\alpha + 1) = [(-\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3] + [(-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3] =2\alpha + 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Vektor}\hspace{0.15cm}"22"\hspace{0.05cm},$$
- $${\rm Inv_A}("22") \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(2\alpha + 2) = [(-2\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3] + [(-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3] =\alpha + 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Vektor}\hspace{0.15cm}"11"\hspace{0.05cm}.$$
Demzufolge sind nur die beiden ersten Lösungsvorschläge richtig.
Die Aufgabe kann aber auch ohne Rechnung allein anhand der Additionstabelle gelöst werden.
- Beispielsweise findet man die Inverse zu „$22$”, indem man in der letzten Zeile die Spalte mit dem Eintrag „$00$” sucht.
- Man findet die mit „$11$” bezeichnete Spalte und damit ${\rm Inv_A}(„22”) = \, „11”$.
(5) Die Multiplikation von $\alpha$ (Vektor „$10$”) mit sich selbst ergibt $\alpha^2$.
- Würde der erste Lösungsvorschlag gültig sein, so müsste sich aus der Bedingung $\alpha^2 + 2 = 0$ und damit $\alpha^2 = (-2) \, {\rm mod} \, 3 = 1$ ergeben, also der Vektor „$01$”.
- Geht man vom zweiten Lösungsvorschlag aus, so folgt aus der Bedingung $\alpha^2 + 2\alpha + 2 = 0$ in der Polynomschreibweise
- $$\alpha^2 = [(-2\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3] + [(-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3] = \alpha + 1 $$
- und damit der Koeffizientenvektor „$11$”.
In der Multiplikationstabelle findet man in Zeile 4, Spalte 4 genau den Eintrag „$11$” → Richtig ist also der Lösungsvorschlag 2.
(6) Die multiplikative Inverse zu „$12$” findet man in der Zeile 6 der Multiplikationstabelle als diejenige Spalte mit dem Eintrag „$01$” ⇒ Der Lösungsvorschlag 2 ist also richtig im Gegensatz zu Vorschlag 3. Es gilt nämlich ${\rm Inv_M}(„21”) = \, „20”$.
Wir überprüfen diese Ergebnisse unter Berücksichtigung von $\alpha^2 + 2\alpha + 2 = 0$ durch Multiplikationen:
- $$"12" \cdot "10" \hspace{0.15cm} \Rightarrow \hspace{0.15cm} (\alpha + 2) \cdot \alpha = \alpha^2 + 2\alpha = (-2\alpha-2) + 2\alpha = -2 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = 1 \hspace{0.15cm} \Rightarrow \hspace{0.15cm} {\rm Vektor}\hspace{0.15cm}"01" \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm multiplikative \hspace{0.15cm}Inverse}\hspace{0.05cm}.$$
- $$"21" \cdot "12" \hspace{0.15cm} \Rightarrow \hspace{0.15cm} (2\alpha + 1) \cdot (\alpha + 2) = 2 \alpha^2 + \alpha + 4\alpha + 2 = 2 \alpha^2 + 5\alpha + 2 = 2 \cdot (-2\alpha - 2) + 5\alpha + 2 = (\alpha - 2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = \alpha +1 $$
- $$\hspace{2.725cm} \Rightarrow \ {\rm Vektor}\hspace{0.15cm}"11" \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm keine \hspace{0.15cm}multiplikative \hspace{0.15cm}Inverse}\hspace{0.05cm}.$$
Der Lösungsvorschlag 1 ist deshalb nicht richtig, weil es für „$00$” keine multiplikative Inverse gibt.
(7) Die beiden Ausdrücke stimmen überein ⇒ JA, wie die folgenden Berechnungen zeigen:
- $$("20" + "12") \ \cdot "12" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "02"\cdot "12" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "21"\hspace{0.05cm},$$
- $$"20" \cdot "12" + "12" \cdot "12" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "02" + "22" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "21"\hspace{0.05cm}.$$
Das bedeutet: Das Distributivgesetz wurde zumindest an einem einzigen Beispiel nachgewiesen.