Aufgaben:Aufgabe 2.5: Drei Varianten von GF(2 hoch 4): Unterschied zwischen den Versionen
| Zeile 26: | Zeile 26: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welches Polynom liegt der Tabelle (A) zugrunde? |
| − | |type=" | + | |type="()"} |
| − | + | + | + $p(x) = x^4 + x + 1$, |
| − | - | + | - $p(x) = x^4 + x^3 + 1$. |
| − | { | + | {Welches Polynom liegt der Tabelle (B) zugrunde? |
| − | |type=" | + | |type="()"} |
| − | + | + | - $p(x) = x^4 + x + 1$, |
| − | + | + $p(x) = x^4 + x^3 + 1$. | |
| − | { | + | {Berechnen Sie die in der Tabelle (B) fehlenden Einträge. Welche der folgenden Angaben sind richtig? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $\alpha^5 = \alpha^3 + \alpha + 1$ |
| − | |||
{Multiple-Choice | {Multiple-Choice | ||
| − | |type=" | + | |type="()"} |
+ correct | + correct | ||
- false | - false | ||
Version vom 15. Dezember 2017, 22:23 Uhr
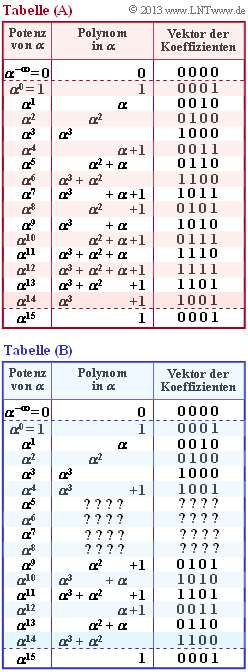
Irreduzible und primitive Polynome haben große Bedeutung für die Beschreibung von Verfahren zur Fehlerkorrektur. In LN97 findet man zum Beispiel die folgenden irreduziblen Polynome vom Grad $m = 4$:
- $p(x) = x^4 + x +1$,
- $p(x) = x^4 + x^3 + 1$,
- $p(x) = x^4 + x^3 + x^2 + x + 1$.
Die beiden ersten Polynome sind auch primitiv. Dies erkennt man aus den Potenztabellen, die rechts angegeben sind – die untere Tabelle (B) allerdings nicht ganz vollständig. Aus beiden Tabellen erkennt man, dass alle Potenzen $\alpha^i$ für $1 ≤ i ≤ 14$ in der Polynomdarstellung ungleich $1$ sind. Erst für $i = 15$ ergibt sich
- $$\alpha^{15} = \alpha^{0} = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}{\rm Koeffizientenvektor\hspace{0.15cm} 0001} \hspace{0.05cm}.$$
Nicht angegeben wird, ob sich die rot hinterlegte Tabelle (A) aus dem Polynom $x^4 + x + 1$ oder aus $x^4 + x^3 + 1$ ergibt. Diese Zuordnungen sollen Sie in den Teilaufgaben (1) und (2) treffen. In der Teilaufgabe (3) sollen Sie zudem die fehlenden Potenzen $\alpha^5, \ \alpha^6, \ \alpha^7$ und $\alpha^8$ in der Tabelle (B) ergänzen.
Die Teilaufgabe (4) bezieht sich auf das ebenfalls irreduzible Polynom $p(x) = x^4 + x^3 + x^2 + x +1$. Entsprechend den oben genannten Kriterien sollen Sie entscheiden, ob dieses Polynom primitiv ist oder nicht.
Hinweis:
- Die Aufgabe gehört ebenfalls zum Themengebiet des Kapitels Erweiterungskörper.
Fragebogen
Musterlösung