Aufgaben:Aufgabe 2.3: Noch ein weiterer Mehrwegekanal: Unterschied zwischen den Versionen
| Zeile 68: | Zeile 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Es gilt hier $r(\tau) = s(\tau) ∗ h(\tau)$, wobei $s(\tau)$ ein Rechteckimpuls der Dauer $T = 5 \ \rm | + | '''(1)''' Es gilt hier $r(\tau) = s(\tau) ∗ h(\tau)$, wobei $s(\tau)$ ein Rechteckimpuls der Dauer $T = 5 \ \rm µ s$ bezeichnet und die Impulsantwort $h(\tau)$ sich allgemein aus $M$ gewichteten Diracfunktionen bei $\tau_1, \tau_2, \ \text{...} \ , \tau_M$ zusammensetzt. |
| + | |||
| + | Das skizzierte Ausgangssignal $r(\tau)$ kann sich nur ergeben, falls | ||
* $\tau_1 = 0$ ist (sonst würde $r(\tau)$ nicht bei $\tau = 0$ beginnen), | * $\tau_1 = 0$ ist (sonst würde $r(\tau)$ nicht bei $\tau = 0$ beginnen), | ||
| − | * $\tau_M = 10 \ \rm | + | * $\tau_M = 10 \ \rm µ s$ ist (daraus ergibt sich der Rechteckverlauf zwischen $10 \ \rm µ s$ und $15 \ \rm µ s$), |
| − | * dazwischen noch eine Diracfunktion bei $\tau_2 = 2 \ \rm | + | * dazwischen noch eine Diracfunktion bei $\tau_2 = 2 \ \rm µ s$ auftritt. |
| − | Das heißt: Die Impulsantwort setzt sich hier aus $\underline {M = 3}$ Diracfunktionen zusammen. | + | Das heißt: Die Impulsantwort setzt sich hier aus $\underline {M = 3}$ Diracfunktionen zusammen. |
'''(2)''' Wie bereits bei der ersten Teilaufgabe berechnet, erhält man | '''(2)''' Wie bereits bei der ersten Teilaufgabe berechnet, erhält man | ||
| − | :$$\tau_1 \hspace{0.1cm} \underline {= 0}\hspace{0.05cm},\hspace{0.2cm}\tau_2 \hspace{0.1cm} \underline {= 2\,{\rm | + | :$$\tau_1 \hspace{0.1cm} \underline {= 0}\hspace{0.05cm},\hspace{0.2cm}\tau_2 \hspace{0.1cm} \underline {= 2\,{\rm µ s}}\hspace{0.05cm},\hspace{0.2cm}\tau_3 \hspace{0.1cm} \underline {= 10\,{\rm µ s}}\hspace{0.05cm}.$$ |
| + | |||
'''(3)''' Vergleicht man Eingang $s(\tau)$ und Ausgang $r(\tau)$, so gelangt man zu folgenden Ergebnissen: | '''(3)''' Vergleicht man Eingang $s(\tau)$ und Ausgang $r(\tau)$, so gelangt man zu folgenden Ergebnissen: | ||
| − | * Intervall $0 < \tau < 2 \ {\rm | + | * Intervall $0 < \tau < 2 \ {\rm µ s} \text{:} \, s(\tau) = s_0, \hspace{1cm} r(\tau) = 0.75 \cdot s_0 \,\,\Rightarrow\,\, k_1 \ \underline {= 0.75}$, |
| − | * Intervall $2 \ {\rm | + | * Intervall $2 \ {\rm µ s} < \tau < 5 \ {\rm µ s} \text{:} \, \hspace{2.4cm} r(\tau) =(k_1 + k_2) \cdot s_0 = 0.25 \cdot s_0 \Rightarrow k_2 \ \underline {= \, –0.50}$, |
| − | * Intervall $10 \ {\rm | + | * Intervall $10 \ {\rm µ s} < \tau < 15 \ {\rm µ s} \text{:} \, \hspace{1.95cm} r(\tau) =k_3 \cdot s_0 = 0.25 \cdot s_0 \,\Rightarrow\, k_3 \ \underline {= 0.25}$. |
| + | |||
| Zeile 120: | Zeile 124: | ||
'''(6)''' Der soeben berechnete Frequenzgang kann für die Frequenz $f = 250 \ \rm kHz$ wie folgt dargestellt werden: | '''(6)''' Der soeben berechnete Frequenzgang kann für die Frequenz $f = 250 \ \rm kHz$ wie folgt dargestellt werden: | ||
| + | [[Datei:P_ID2162__Mob_A_2_3e.png|right|frame|Betragsfrequenzgang beim Dreiwegekanal]] | ||
:$$H(f = 250\,{\rm kHz})= k_1 + k_2 \cdot {\rm e}^{-{\rm j}\cdot \pi}+ k_3 \cdot {\rm e}^{-{\rm j}\cdot 5\pi} = k_1 - k_2 - k_3 | :$$H(f = 250\,{\rm kHz})= k_1 + k_2 \cdot {\rm e}^{-{\rm j}\cdot \pi}+ k_3 \cdot {\rm e}^{-{\rm j}\cdot 5\pi} = k_1 - k_2 - k_3 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Wählt man nun | |
| − | Wählt man nun $k_3 = k_1 - k_2 = 0.75 + 0.50\hspace{0.1cm} \underline {= 1.25}\hspace{0.05cm}$ so ergibt sich $|H(f = 250 \ \rm kHz)| = 0$ und damit der für diese Signalfrequenz ungünstigste Wert. | + | :$$k_3 = k_1 - k_2 = 0.75 + 0.50\hspace{0.1cm} \underline {= 1.25}\hspace{0.05cm},$$ |
| + | so ergibt sich $|H(f = 250 \ \rm kHz)| = 0$ und damit der für diese Signalfrequenz ungünstigste Wert. | ||
Die Grafik zeigt $|H(f)|$ im Bereich zwischen $0$ und $500 \ \rm kHz$: | Die Grafik zeigt $|H(f)|$ im Bereich zwischen $0$ und $500 \ \rm kHz$: | ||
| − | *Die blaue Kurve gilt für $k_3 = 0.25$ entsprechend den Vorgaben von Teilaufgabe (4). | + | *Die blaue Kurve gilt für $k_3 = 0.25$ entsprechend den Vorgaben von Teilaufgabe '''(4)'''. |
*Die rote Kurve gilt für $k_3 = 1.25$, dem ungünstigsten Wert für $f = 250 \ \rm kHz$. | *Die rote Kurve gilt für $k_3 = 1.25$, dem ungünstigsten Wert für $f = 250 \ \rm kHz$. | ||
Version vom 11. April 2019, 17:30 Uhr
Wir betrachten einen Mehrwegekanal, der durch folgende Impulsantwort charakterisiert wird:
- $$h(\tau, \hspace{0.05cm} t) = h(\tau) = \sum_{m = 1}^{M} k_m \cdot \delta( \tau - \tau_m) \hspace{0.05cm}.$$
Alle Koeffizienten $k_{m}$ seien reell (positiv oder negativ). Weiterhin ist anzumerken:
- Aus der Angabe $h(\tau, \hspace{0.05cm}t) = h(\tau)$ erkennt man, dass der Kanal zeitinvariant ist.
- Allgemein weist der Kanal $M$ Pfade auf. Der $M$–Wert soll aus der Grafik bestimmt werden.
- Für die Verzögerungszeiten gelten folgende Relationen: $\tau_1 < \tau_2 < \tau_3 < \ \text{...}$
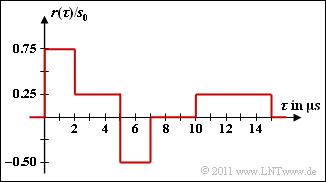
Die Grafik zeigt das Ausgangssignal $r(\tau)$ des Kanals, wenn am Eingang folgendes Sendesignal anliegt (dargestellt im äquivalenten Tiefpassbereich):
- $$s(\tau) = \left\{ \begin{array}{c} s_0\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le \tau < 5\,{\rm µ s}, \\ {\rm sonst}. \\ \end{array}$$
Gesucht wird die dazugehörige Impulsantwort $h(\tau)$ sowie die Übertragungsfunktion $H(f)$.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Mehrwegeempfang beim Mobilfunk.
- Gehen Sie bei der Lösung der Teilaufgabe (1) davon aus, dass sich die Impulsantwort $h(\tau)$ über 5 Mikrosekunden erstreckt.
Fragebogen
Musterlösung
Das skizzierte Ausgangssignal $r(\tau)$ kann sich nur ergeben, falls
- $\tau_1 = 0$ ist (sonst würde $r(\tau)$ nicht bei $\tau = 0$ beginnen),
- $\tau_M = 10 \ \rm µ s$ ist (daraus ergibt sich der Rechteckverlauf zwischen $10 \ \rm µ s$ und $15 \ \rm µ s$),
- dazwischen noch eine Diracfunktion bei $\tau_2 = 2 \ \rm µ s$ auftritt.
Das heißt: Die Impulsantwort setzt sich hier aus $\underline {M = 3}$ Diracfunktionen zusammen.
(2) Wie bereits bei der ersten Teilaufgabe berechnet, erhält man
- $$\tau_1 \hspace{0.1cm} \underline {= 0}\hspace{0.05cm},\hspace{0.2cm}\tau_2 \hspace{0.1cm} \underline {= 2\,{\rm µ s}}\hspace{0.05cm},\hspace{0.2cm}\tau_3 \hspace{0.1cm} \underline {= 10\,{\rm µ s}}\hspace{0.05cm}.$$
(3) Vergleicht man Eingang $s(\tau)$ und Ausgang $r(\tau)$, so gelangt man zu folgenden Ergebnissen:
- Intervall $0 < \tau < 2 \ {\rm µ s} \text{:} \, s(\tau) = s_0, \hspace{1cm} r(\tau) = 0.75 \cdot s_0 \,\,\Rightarrow\,\, k_1 \ \underline {= 0.75}$,
- Intervall $2 \ {\rm µ s} < \tau < 5 \ {\rm µ s} \text{:} \, \hspace{2.4cm} r(\tau) =(k_1 + k_2) \cdot s_0 = 0.25 \cdot s_0 \Rightarrow k_2 \ \underline {= \, –0.50}$,
- Intervall $10 \ {\rm µ s} < \tau < 15 \ {\rm µ s} \text{:} \, \hspace{1.95cm} r(\tau) =k_3 \cdot s_0 = 0.25 \cdot s_0 \,\Rightarrow\, k_3 \ \underline {= 0.25}$.
(4) Mit dem Verschiebungssatz erhält man für die Fouriertransformatierte der Impulsantwort $h(\tau)$:
- $$h(\tau) = k_1 \cdot \delta( \tau) + k_2 \cdot \delta( \tau - \tau_2)+ k_3 \cdot \delta( \tau - \tau_3) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}H(f) = k_1 + k_2 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_2}+ k_3 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_3} \hspace{0.05cm}. $$
Durch Analyse der einzelnen Beiträge kommt man zu folgendem Ergebnis:
- Der erste Anteil ist konstant ⇒ Periode $f_1 → ∞$.
- Der zweite Anteil ist periodisch mit $f_2 = 1/\tau_2 = 500 \ \rm kHz$.
- Der dritte Anteil ist periodisch mit $f_3 = 1/\tau_3 = 100 \ \rm kHz$.
⇒ Insgesamt ist damit $H(f)$ periodisch mit $f_0 \ \underline {= 500 \ \rm kHz}$.
(5) Mit $A = 2\pi f \cdot \tau_2$ und $B = 2\pi f \cdot \tau_3$ erhält man:
- $$|H(f)|^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} H(f) \cdot H^{\star}(f)= \left [ \frac {3}{4} - \frac {1}{2} \cdot {\rm e}^{-{\rm j}A} + \frac {1}{4} \cdot {\rm e}^{-{\rm j}B}\right ] \left [ \frac {3}{4} - \frac {1}{2} \cdot {\rm e}^{{\rm j}A} + \frac {1}{4} \cdot {\rm e}^{{\rm j}B}\right ]$$
- $$\Rightarrow \hspace{0.3cm} |H(f)|^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {9}{16 }- \frac {3 {\rm e}^{{\rm j}A}}{8} +\frac {3{\rm e}^{{\rm j}B}}{16} - \frac {3{\rm e}^{-{\rm j}A}}{8} +\frac {1}{4}- \frac {{\rm e}^{{\rm j}(B-A)}}{8} +\frac {3{\rm e}^{-{\rm j}B}}{16} - \frac {{\rm e}^{{\rm j}(A-B)}}{8} +\frac{1}{16 }=$$
- $$\hspace{2.1cm} \ = \ \hspace{-0.1cm}\frac {7}{8 }- \frac {3}{8} \cdot \left [ {\rm e}^{{\rm j}A} + {\rm e}^{-{\rm j}A}\right ]+ \frac {3}{16} \cdot \left [ {\rm e}^{{\rm j}B} + {\rm e}^{-{\rm j}B}\right ]- \frac {1}{8} \cdot \left [ {\rm e}^{{\rm j}(B-A)} + {\rm e}^{-{\rm j}(B-A)}\right ]\hspace{0.05cm}.$$
Daraus ergibt sich mit dem Satz von Euler unter Berücksichtigung der Frequenzperiodizität:
- $$|H(f)|= \sqrt{\frac {7}{8 }- \frac {3}{4} \cdot \cos( 2 \pi f \tau_2) + \frac {3}{8} \cdot \cos( 2 \pi f \tau_3)- \frac {1}{4} \cdot \cos( 2 \pi f (\tau_3 - \tau_2))}$$
- $$\Rightarrow \hspace{0.3cm} |H(f = 0)|\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{\frac {7}{8 }- \frac {3}{4} + \frac {3}{8} - \frac {1}{4} } = \sqrt{0.25}\hspace{0.1cm} \underline {= 0.5} = |H(f = 500\,{\rm kHz})|$$
- $$|H(f = 250\,{\rm kHz})|\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{\frac {7}{8 }- \frac {3}{4} \cdot \cos( \pi ) + \frac {3}{8} \cdot \cos( 5 \pi )- \frac {1}{4} \cdot \cos( 4 \pi )} \hspace{0.1cm} \underline {= 1}\hspace{0.05cm}.$$
(6) Der soeben berechnete Frequenzgang kann für die Frequenz $f = 250 \ \rm kHz$ wie folgt dargestellt werden:
- $$H(f = 250\,{\rm kHz})= k_1 + k_2 \cdot {\rm e}^{-{\rm j}\cdot \pi}+ k_3 \cdot {\rm e}^{-{\rm j}\cdot 5\pi} = k_1 - k_2 - k_3 \hspace{0.05cm}.$$
Wählt man nun
- $$k_3 = k_1 - k_2 = 0.75 + 0.50\hspace{0.1cm} \underline {= 1.25}\hspace{0.05cm},$$
so ergibt sich $|H(f = 250 \ \rm kHz)| = 0$ und damit der für diese Signalfrequenz ungünstigste Wert.
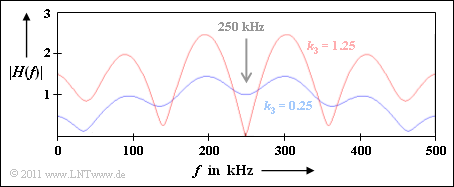
Die Grafik zeigt $|H(f)|$ im Bereich zwischen $0$ und $500 \ \rm kHz$:
- Die blaue Kurve gilt für $k_3 = 0.25$ entsprechend den Vorgaben von Teilaufgabe (4).
- Die rote Kurve gilt für $k_3 = 1.25$, dem ungünstigsten Wert für $f = 250 \ \rm kHz$.