Aufgaben:Aufgabe 2.2Z: Realer Zweiwegekanal

• Zurück zum Buch

Zweiwege–Szenario

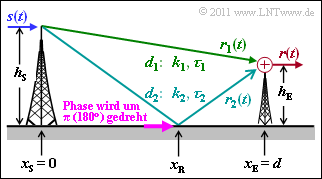
Betrachtet wird das skizzierte Szenario, bei dem das Sendesignal $s(t)$ die Antenne des Empfängers über zwei Wege erreicht:

$$r(t) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} r_1(t) + r_2(t) =$$

$$\hspace{-0.15cm} \ = \ \hspace{-0.15cm}k_1 \cdot s( t - \tau_1) + k_2 \cdot s( t - \tau_2) \hspace{0.05cm}.$$

Dabei ist zu beachten:

• Die Laufzeiten $\tau_1$ und $\tau_2$ auf Haupt– und Nebenpfad können aus den Pfadlängen $d_1$ und $d_2$ unter Verwendung der Lichtgeschwindigkeit $c = 3 \cdot 10^8 \ \rm m/s$ berechnet werden.
• Die Amplitudenfaktoren $k_1$ und $k_2$ sollen vereinfachend gemäß dem Pfadverlustmodell mit dem Pfadverlustexponenten $\gamma = 2$ angenommen werden (Freiraumdämpfung).
• Die Höhe der Sendeantenne ist $h_{\rm S} = 500 \ \rm m$, die der Empfangsantenne $h_{\rm E} = 30 \ \rm m$. Die Antennen stehen im Abstand von $d = 10 \ \rm km$.
• Die Reflektion auf dem Nebenpfad führt zu einer Phasenänderung um $\pi$, so dass man die Teilsignale subtrahieren muss. Dies wird durch einen negativen $k_2$–Wert berücksichtigt.

Hinweis:

• Die Aufgabe gehört zum Themengebiet des Kapitels Mehrwegeempfang beim Mobilfunk.

Fragebogen

1

Berechnen Sie die Distanz $d_1$ des direkten Pfades.

$d_1 \ = \ $ $\ \rm m$

2

Berechnen Sie die Länge $d_2$ des Umwegpfades.

$d_2 \ = \ $ $\ \rm m$

3

Welche Differenzen $\Delta d = d_2 \ –d_1$ und $\Delta \tau = \tau_2 \ –\tau_1$ (Laufzeit) ergeben sich?

${\rm exakt} \text{:} \hspace{0.4cm} \Delta d \ = \ $ $\ \rm m$

$\hspace{1.5cm} \Delta \tau \ = \ $ $\ \rm ns$

4

Welche Gleichung ergibt sich für die Laufzeitdifferenz $\Delta \tau$ mit der für kleine $\epsilon$ gültigen Näherung $\sqrt{(1 + \epsilon)} \approx 1 + \epsilon/2$?

	$\Delta \tau = (h_{\rm S} \ –h_{\rm E})/d$,
	$\Delta \tau = (h_{\rm S} \ –h_{\rm E})/(c \cdot d)$,
	$\Delta \tau = 2 \cdot h_{\rm S} \cdot h_{\rm E}/(c \cdot d)$.

5

Welche Aussagen treffen für die Amplitudenkoeffizienten $k_1$ und $k_2$ zu?

	Die Koeffizienten $k_1$und $k_2$ sind betragsmäßig nahezu gleich.
	Die Beträge $|k_1|$ und $|k_2|$ unterscheiden sich deutlich.
	Die Koeffizienten $k_1$ und $k_2$ unterscheiden sich im Vorzeichen.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)