Aufgaben:Aufgabe 2.2Z: Galoisfeld GF(5): Unterschied zwischen den Versionen
| Zeile 85: | Zeile 85: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Das neutrale Element hinsichtlich Addition (genannt $N_{\rm A}$ | + | '''(1)''' Das neutrale Element hinsichtlich Addition $($genannt $N_{\rm A})$ muss für alle Elemente $z_i (i = 0, \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ q-1)$ die folgende Gleichung erfüllen: |
:$$z_i + N_{\rm A} = N_{\rm A} + z_i = z_i\hspace{0.05cm}.$$ | :$$z_i + N_{\rm A} = N_{\rm A} + z_i = z_i\hspace{0.05cm}.$$ | ||
| − | Aus der Additionstabelle folgt $N_{\rm A} \ \underline{= d}$. | + | *Aus der Additionstabelle folgt $N_{\rm A} \ \underline{= \rm d}$. |
| − | '''(2)''' Dagegen erfüllt das neutrale Element der Multiplikation $(N_{\rm M})$ für alle Elemente $z_i (i = 1,\hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ q-1)$ die folgende Bedingung: | + | '''(2)''' Dagegen erfüllt das neutrale Element der Multiplikation $(N_{\rm M})$ für alle Elemente $z_i (i = 1,\hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ q-1)$ die folgende Bedingung: |
:$$z_i \cdot N_{\rm M} = N_{\rm M}\cdot z_i = z_i\hspace{0.05cm}.$$ | :$$z_i \cdot N_{\rm M} = N_{\rm M}\cdot z_i = z_i\hspace{0.05cm}.$$ | ||
| − | Aus der Multiplikationstabelle erkennt man $N_{\rm M} \ \underline{= c}$. | + | *Aus der Multiplikationstabelle erkennt man $N_{\rm M} \ \underline{= \rm c}$. |
| − | '''(3)''' Das Kommutativgesetz ist bei diesem Galoisfeld in <u>beiden Fällen</u> (Addition und Multiplikation) erfüllt, da Additionstabelle und Multiplikationstabelle jeweils symmetrisch zur Tabellendiagonalen sind. | + | '''(3)''' Das Kommutativgesetz ist bei diesem Galoisfeld in <u>beiden Fällen</u> (Addition und Multiplikation) erfüllt, <br> da Additionstabelle und Multiplikationstabelle jeweils symmetrisch zur Tabellendiagonalen sind. |
| − | '''(4)''' Betrachten wir zunächst den ersten Ausdruck. Bei Gültigkeit des Distributivgesetzes muss gelten: | + | '''(4)''' Betrachten wir zunächst den ersten Ausdruck. |
| − | :$$a \cdot (b+c) = a \cdot b+ a \cdot c \hspace{0.05cm}.$$ | + | *Bei Gültigkeit des Distributivgesetzes muss gelten: |
| + | :$$\rm a \cdot (b+c) = a \cdot b+ a \cdot c \hspace{0.05cm}.$$ | ||
| − | Für die linke Seite erhält man: | + | *Für die linke Seite erhält man: |
| − | :$$a \cdot (b+c) = a \cdot a =e \hspace{0.05cm},$$ | + | :$$\rm a \cdot (b+c) = a \cdot a =e \hspace{0.05cm},$$ |
| − | und für die rechte Seite: | + | :und für die rechte Seite: |
| − | :$$a \cdot b+ a \cdot c = c + a = e\hspace{0.05cm}.$$ | + | :$$\rm a \cdot b+ a \cdot c = c + a = e\hspace{0.05cm}.$$ |
| − | Das Distributivgesetz ist hier ebenso erfüllt wie auch bei den beiden anderen vorgegebenen Ausdrücken: | + | *Das Distributivgesetz ist hier ebenso erfüllt wie auch bei den beiden anderen vorgegebenen Ausdrücken: |
| − | :$$d \cdot (b+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot a =d \hspace{0.05cm}, \hspace{0.5cm}d \cdot b+ d \cdot c = d + d = d\hspace{0.05cm},$$ | + | :$$\rm d \cdot (b+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot a =d \hspace{0.05cm}, \hspace{0.5cm}d \cdot b+ d \cdot c = d + d = d\hspace{0.05cm},$$ |
| − | :$$e \cdot (a+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} e \cdot e =c \hspace{0.05cm}, \hspace{0.5cm}e \cdot a+ e \cdot c = b + e = c\hspace{0.05cm}.$$ | + | :$$\rm e \cdot (a+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} e \cdot e =c \hspace{0.05cm}, \hspace{0.5cm}e \cdot a+ e \cdot c = b + e = c\hspace{0.05cm}.$$ |
| − | <u>Alle Lösungsvorschläge</u> treffen zu. | + | <u>Alle Lösungsvorschläge</u> treffen zu. |
| Zeile 122: | Zeile 123: | ||
[[Datei:P_ID2495__KC_Z_2_2e.png|right|frame|Umgewandelte Operationstabellen]] | [[Datei:P_ID2495__KC_Z_2_2e.png|right|frame|Umgewandelte Operationstabellen]] | ||
'''(5)''' | '''(5)''' | ||
| − | Das Nullelement $N_{\rm A} = d$ wird zu $N_{\rm A} = 0 \Rightarrow d = 0$, das Einselelement $N_{\rm M} = c$ zu $N_{\rm M} = 1 \Rightarrow c = 1$. Die weiteren Elemente $a, \ b$ und $e$ können modulo $5$ aus der Additionstabelle oder der Multiplikationstabelle bestimmt werden. | + | Das Nullelement $N_{\rm A} = \rm d$ wird zu $N_{\rm A} = 0 \ \Rightarrow \ d = 0$, das Einselelement $N_{\rm M} = c$ zu $N_{\rm M} = 1 \ \Rightarrow \ \rm c = 1$. |
| − | + | ||
| + | *Die weiteren Elemente $\rm a, \ b$ und $\rm e$ können modulo $5$ aus der Additionstabelle oder der Multiplikationstabelle bestimmt werden. | ||
| − | + | *Zum Beispiel folgt aus der ersten Zeile der Additionstabelle | |
| − | :$$a | + | :$$\rm (a + b) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = d = 0 \hspace{0.05cm}.$$ |
| − | + | *Da sowohl $\rm a$ als auch $\rm b$ nicht $0$ oder $1$ sein können (da diese bereits für $\rm c$ und $\rm d$ vergeben sind), ergibt sich als Folgerung: | |
| − | :$$ | + | :$$\rm a = 2, \hspace{0.3cm} b = 3 \hspace{0.5cm}{\rm oder}\hspace{0.5cm} a = 3, \hspace{0.3cm} b = 2\hspace{0.05cm}.$$ |
| − | Aus | + | *Aus der zweiten Zeile der Additionstabelle folgt beispielsweise: |
| + | :$$\rm (b + b) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = e \hspace{0.05cm}.$$ | ||
| − | Also erhält man als Endergebnis: | + | *Aus $\rm b = 3$ ergäbe sich $\rm e = 1$. Dies ist aber wiederum nicht möglich, da bereits $\rm c = 1$ festgelegt wurde. |
| − | :$$a \hspace{0.15cm}\underline{= 3}\hspace{0.05cm},\hspace{0.2cm}b \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},\hspace{0.2cm} | + | |
| + | *Also erhält man als Endergebnis: | ||
| + | :$$\rm a \hspace{0.15cm}\underline{= 3}\hspace{0.05cm},\hspace{0.2cm}b \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},\hspace{0.2cm} | ||
c \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},\hspace{0.2cm}d \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm} | c \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},\hspace{0.2cm}d \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm} | ||
e \hspace{0.15cm}\underline{= 4}\hspace{0.05cm}.$$ | e \hspace{0.15cm}\underline{= 4}\hspace{0.05cm}.$$ | ||
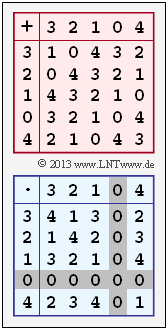
| − | Die Grafik zeigt die Additions– und die Multiplikationstabelle für diese Zahlenmenge. | + | *Die Grafik zeigt die Additions– und die Multiplikationstabelle für diese Zahlenmenge. |
| + | |||
| + | '''(6)''' Zutreffend sind die <u>Aussagen 1 und 4</u>: | ||
| + | *Man erkennt in der Additionstabelle in jeder Zeile und Spalte genau ein "$\rm d = 0$". Das heißt: | ||
| − | + | *Für alle $z_i ∈ \{0, \, 1, \, 2, \, 3, \, 4\}$ existiert eine eindeutige additive Inverse. | |
| − | * | ||
| − | Die multiplikative Inverse erkennt man in der Multiplikationstabelle durch den Eintrag $c = 1$. Die multiplikativen Inversen lauten wie folgt: | + | *Die multiplikative Inverse erkennt man in der Multiplikationstabelle durch den Eintrag $\rm c = 1$. Die multiplikativen Inversen lauten wie folgt: |
| − | :$${\rm Zeile \hspace{0.15cm}1\text{:}}\hspace{0.25cm} {\rm Inv_M}(a=3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} b = 2 \hspace{0.05cm},$$ | + | :$${\rm Zeile \hspace{0.15cm}1\text{:}}\hspace{0.25cm} {\rm Inv_M}(a=3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \rm b = 2 \hspace{0.05cm},$$ |
| − | :$${\rm Zeile\hspace{0.15cm} 2\text{:}}\hspace{0.25cm} {\rm Inv_M}(b=2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} a=3 \hspace{0.05cm},$$ | + | :$${\rm Zeile\hspace{0.15cm} 2\text{:}}\hspace{0.25cm} {\rm Inv_M}(b=2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \rm a=3 \hspace{0.05cm},$$ |
| − | :$${\rm Zeile\hspace{0.15cm} 3\text{:}}\hspace{0.25cm} {\rm Inv_M}(c=1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} c=1 \hspace{0.05cm},$$ | + | :$${\rm Zeile\hspace{0.15cm} 3\text{:}}\hspace{0.25cm} {\rm Inv_M}(c=1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \rm c=1 \hspace{0.05cm},$$ |
| − | :$${\rm Zeile\hspace{0.15cm} 5\text{:}}\hspace{0.25cm} {\rm Inv_M}(e=4) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} e=4 \hspace{0.05cm}.$$ | + | :$${\rm Zeile\hspace{0.15cm} 5\text{:}}\hspace{0.25cm} {\rm Inv_M}(e=4) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \rm e=4 \hspace{0.05cm}.$$ |
| − | Für das Nullelement $d = 0$ existiert dagegen keine multiplikative Inverse. | + | *Für das Nullelement $\rm d = 0$ existiert dagegen keine multiplikative Inverse. |
'''(7)''' Bezüglich der primitiven Elemente erhält man | '''(7)''' Bezüglich der primitiven Elemente erhält man | ||
| − | :$$a \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 3 \hspace{0.05cm},\hspace{0.2cm} a^2 = 9 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 | + | :$$\rm a \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 3 \hspace{0.05cm},\hspace{0.2cm} a^2 = 9 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 |
\hspace{0.05cm},\hspace{0.2cm} a^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} a^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm primitiv}\hspace{0.05cm},$$ | \hspace{0.05cm},\hspace{0.2cm} a^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} a^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm primitiv}\hspace{0.05cm},$$ | ||
:$$b \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \hspace{0.05cm},\hspace{0.2cm} b^2 = 4 | :$$b \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \hspace{0.05cm},\hspace{0.2cm} b^2 = 4 | ||
| Zeile 163: | Zeile 170: | ||
\hspace{0.05cm},\hspace{0.2cm} e^3 = \hspace{0.05cm} ...\hspace{0.05cm}= 4\hspace{0.05cm},\hspace{0.2cm} e^4 =\hspace{0.05cm} ...\hspace{0.05cm} = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm nicht\hspace{0.15cm} primitiv}\hspace{0.05cm}.$$ | \hspace{0.05cm},\hspace{0.2cm} e^3 = \hspace{0.05cm} ...\hspace{0.05cm}= 4\hspace{0.05cm},\hspace{0.2cm} e^4 =\hspace{0.05cm} ...\hspace{0.05cm} = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm nicht\hspace{0.15cm} primitiv}\hspace{0.05cm}.$$ | ||
| − | Von der Menge $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\}$ sind „$2$” und „$3$” primitive Elemente ⇒ <u>Lösungsvorschläge 1 und 2</u>. | + | *Von der Menge $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\}$ sind „$2$” und „$3$” primitive Elemente ⇒ <u>Lösungsvorschläge 1 und 2</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 28. August 2022, 17:22 Uhr
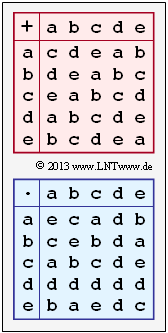
Wie in der "Aufgabe 2.2" betrachten wir einen endlichen Körper der Ordnung $q = 5$ und damit das Galoisfeld
- $$\rm GF(5) = \{{a}, { b},{c},{d},{e}\}\hspace{0.05cm}.$$
Über die Elemente werden weiter keine Aussagen getroffen. Es können sowohl ganze Zahlen sein oder irgendwelche mathematischen Ausdrücke.
Das Galoisfeld wird ausschließlich bestimmt durch
- eine Additionstabelle modulo 5,
- eine Multiplikationstabelle modulo 5.
Die wichtigsten Eigenschaften eines Galoisfeldes sind auf der ersten Theorieseite zusammengestellt. Hier wird Bezug genommen auf
- das Kommutativ– und das Distributivgesetz,
- die neutralen Elemente von Addition und Multiplikation,
- die inversen Elemente von Addition und Multiplikation, sowie
- die Bestimmung primitiver Elemente.
Im vorliegenden Beispiel wäre $\beta$ ein primitives Element, wenn $\beta^2, \ \beta^3$ und $\beta^4$ $($allgemein: $\beta^{q-1})$ die übrigen Elemente des Galoisfeldes $\rm GF(5)$ mit Ausnahme des Nullelementes ergeben.
Hinweis: Die Aufgabe bezieht ich auf das Kapitel "Einige Grundlagen der Algebra".
Fragebogen
Musterlösung
- $$z_i + N_{\rm A} = N_{\rm A} + z_i = z_i\hspace{0.05cm}.$$
- Aus der Additionstabelle folgt $N_{\rm A} \ \underline{= \rm d}$.
(2) Dagegen erfüllt das neutrale Element der Multiplikation $(N_{\rm M})$ für alle Elemente $z_i (i = 1,\hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ q-1)$ die folgende Bedingung:
- $$z_i \cdot N_{\rm M} = N_{\rm M}\cdot z_i = z_i\hspace{0.05cm}.$$
- Aus der Multiplikationstabelle erkennt man $N_{\rm M} \ \underline{= \rm c}$.
(3) Das Kommutativgesetz ist bei diesem Galoisfeld in beiden Fällen (Addition und Multiplikation) erfüllt,
da Additionstabelle und Multiplikationstabelle jeweils symmetrisch zur Tabellendiagonalen sind.
(4) Betrachten wir zunächst den ersten Ausdruck.
- Bei Gültigkeit des Distributivgesetzes muss gelten:
- $$\rm a \cdot (b+c) = a \cdot b+ a \cdot c \hspace{0.05cm}.$$
- Für die linke Seite erhält man:
- $$\rm a \cdot (b+c) = a \cdot a =e \hspace{0.05cm},$$
- und für die rechte Seite:
- $$\rm a \cdot b+ a \cdot c = c + a = e\hspace{0.05cm}.$$
- Das Distributivgesetz ist hier ebenso erfüllt wie auch bei den beiden anderen vorgegebenen Ausdrücken:
- $$\rm d \cdot (b+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot a =d \hspace{0.05cm}, \hspace{0.5cm}d \cdot b+ d \cdot c = d + d = d\hspace{0.05cm},$$
- $$\rm e \cdot (a+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} e \cdot e =c \hspace{0.05cm}, \hspace{0.5cm}e \cdot a+ e \cdot c = b + e = c\hspace{0.05cm}.$$
Alle Lösungsvorschläge treffen zu.
(5) Das Nullelement $N_{\rm A} = \rm d$ wird zu $N_{\rm A} = 0 \ \Rightarrow \ d = 0$, das Einselelement $N_{\rm M} = c$ zu $N_{\rm M} = 1 \ \Rightarrow \ \rm c = 1$.
- Die weiteren Elemente $\rm a, \ b$ und $\rm e$ können modulo $5$ aus der Additionstabelle oder der Multiplikationstabelle bestimmt werden.
- Zum Beispiel folgt aus der ersten Zeile der Additionstabelle
- $$\rm (a + b) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = d = 0 \hspace{0.05cm}.$$
- Da sowohl $\rm a$ als auch $\rm b$ nicht $0$ oder $1$ sein können (da diese bereits für $\rm c$ und $\rm d$ vergeben sind), ergibt sich als Folgerung:
- $$\rm a = 2, \hspace{0.3cm} b = 3 \hspace{0.5cm}{\rm oder}\hspace{0.5cm} a = 3, \hspace{0.3cm} b = 2\hspace{0.05cm}.$$
- Aus der zweiten Zeile der Additionstabelle folgt beispielsweise:
- $$\rm (b + b) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = e \hspace{0.05cm}.$$
- Aus $\rm b = 3$ ergäbe sich $\rm e = 1$. Dies ist aber wiederum nicht möglich, da bereits $\rm c = 1$ festgelegt wurde.
- Also erhält man als Endergebnis:
- $$\rm a \hspace{0.15cm}\underline{= 3}\hspace{0.05cm},\hspace{0.2cm}b \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},\hspace{0.2cm} c \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},\hspace{0.2cm}d \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm} e \hspace{0.15cm}\underline{= 4}\hspace{0.05cm}.$$
- Die Grafik zeigt die Additions– und die Multiplikationstabelle für diese Zahlenmenge.
(6) Zutreffend sind die Aussagen 1 und 4:
- Man erkennt in der Additionstabelle in jeder Zeile und Spalte genau ein "$\rm d = 0$". Das heißt:
- Für alle $z_i ∈ \{0, \, 1, \, 2, \, 3, \, 4\}$ existiert eine eindeutige additive Inverse.
- Die multiplikative Inverse erkennt man in der Multiplikationstabelle durch den Eintrag $\rm c = 1$. Die multiplikativen Inversen lauten wie folgt:
- $${\rm Zeile \hspace{0.15cm}1\text{:}}\hspace{0.25cm} {\rm Inv_M}(a=3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \rm b = 2 \hspace{0.05cm},$$
- $${\rm Zeile\hspace{0.15cm} 2\text{:}}\hspace{0.25cm} {\rm Inv_M}(b=2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \rm a=3 \hspace{0.05cm},$$
- $${\rm Zeile\hspace{0.15cm} 3\text{:}}\hspace{0.25cm} {\rm Inv_M}(c=1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \rm c=1 \hspace{0.05cm},$$
- $${\rm Zeile\hspace{0.15cm} 5\text{:}}\hspace{0.25cm} {\rm Inv_M}(e=4) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \rm e=4 \hspace{0.05cm}.$$
- Für das Nullelement $\rm d = 0$ existiert dagegen keine multiplikative Inverse.
(7) Bezüglich der primitiven Elemente erhält man
- $$\rm a \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 3 \hspace{0.05cm},\hspace{0.2cm} a^2 = 9 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},\hspace{0.2cm} a^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} a^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm primitiv}\hspace{0.05cm},$$
- $$b \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \hspace{0.05cm},\hspace{0.2cm} b^2 = 4 \hspace{0.05cm},\hspace{0.2cm} b^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} b^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm primitiv}\hspace{0.05cm},$$
- $$e \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 4 \hspace{0.05cm},\hspace{0.2cm} e^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},\hspace{0.2cm} e^3 = \hspace{0.05cm} ...\hspace{0.05cm}= 4\hspace{0.05cm},\hspace{0.2cm} e^4 =\hspace{0.05cm} ...\hspace{0.05cm} = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm nicht\hspace{0.15cm} primitiv}\hspace{0.05cm}.$$
- Von der Menge $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\}$ sind „$2$” und „$3$” primitive Elemente ⇒ Lösungsvorschläge 1 und 2.