Aufgaben:Aufgabe 2.1: ZSB-AM mit Cosinus? Oder mit Sinus?

• Zurück zum Buch

Spektrum: Analytischen Signal

Wir betrachten die Amplitudenmodulation des Quellensignals  $q(t)$  mit dem Trägersignal  $z(t)$.  Diese Signale sind wie folgt gegeben:

$$q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N})\hspace{0.05cm},$$

$$z(t) = \hspace{0.15cm}1 \hspace{0.13cm} \cdot \hspace{0.1cm}\cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$

Bekannt ist die Trägerfrequenz mit  $f_{\rm T} = 40\text{ kHz}$.  Die weiteren Systemparameter  $A_{\rm N}$,  $f_{\rm N}$,  $ϕ_{\rm N}$  und  $ϕ_{\rm T}$  sollen in dieser Aufgabe ermittelt werden.

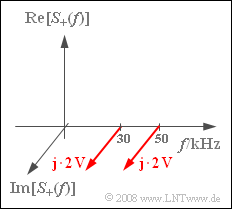
Gegeben ist weiter das Spektrum  $S_+(f)$  des analytischen Signals  $s_+(t)$  am Ausgang des Modulators.  Dieses lautet (siehe Grafik):

$$S_+(f) = {\rm j}\cdot 2\,{\rm V} \cdot \delta ( f - f_{30} )+ {\rm j}\cdot 2\,{\rm V} \cdot \delta ( f - f_{50} )\hspace{0.05cm}.$$

Hierbei sind die Abkürzungen $f_{30} = 30\text{ kHz}$ und $f_{50} = 50\text{ kHz}$ verwendet.

Zur Erinnerung:   Das Spektrum  $S_+(f)$  erhält man aus  $S(f)$, indem man

• die Anteile bei negativen Frequenzen abschneidet und
• bei positiven Frequenzen verdoppelt.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Zweiseitenband-Amplitudenmodulation.
• Bezug genommen wird insbesondere auf die Seiten  Beschreibung im Frequenzbereich  und  Beschreibung im Zeitbereich.
• Gegeben sind folgende trigonometrischen Zusammenhänge:

$$\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \big[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\big ] \hspace{0.05cm}, \hspace{0.5cm} \cos(90^{\circ}- \hspace{0.05cm} \alpha) = \sin(\alpha) \hspace{0.05cm}, \hspace{0.5cm} \cos(90^{\circ}+ \hspace{0.05cm} \alpha) = -\sin(\alpha) \hspace{0.05cm}.$$

Fragebogen

1

Ermitteln Sie das Spektrum  $S(f)$.  Welche der folgenden Aussagen sind richtig?

	$S(f)$  besteht aus vier Diracfunktionen.
	Alle Diracgewichte haben den gleichen Betrag $2\text{ V}$.
	Alle Diracgewichte sind imaginär.

2

Wie lautet das modulierte Signal  $s(t)$?  Welche Aussage trifft zu?

	Es handelt sich um ZSB–AM ohne Träger.
	Es handelt sich um ZSB–AM mit Träger.

3

Geben Sie die Nachrichtenfrequenz $f_{\rm N}$  an.

$f_{\rm N} \ = \ $ $\ \text{kHz}$

4

Bestimmen Sie die Phasen von Quellen– und Trägersignal.

$ϕ_{\rm N} \ = \ $ $\ \text{Grad}$

$ϕ_{\rm T} \ = \ $ $\ \text{Grad}$

5

Wie groß ist die Amplitude des Nachrichtensignals?

$A_{\rm N} \ = \ $ $\ \text{V}$

Musterlösung

Musterlösung

(1)  Richtig sind die Antworten 1 und 3:

• Bei positiven Frequenzen erhält man  $S_+(f)$  aus  $S(f)$  durch Verdoppelung.
• Daraus folgt, dass die Impulsgewichte von  $S(f)$  nur jeweils  ${\rm j} · 1 \text{ V}$  sind.
• Aufgrund des Zuordnungssatzes muss $S(f)$ eine ungerade Funktion sein.
• Deshalb besitzt  $S(f)$  noch zwei weitere Diracfunktionen bei $f = -f_{30}$  und $f = -f_{50}$, jeweils mit dem Gewicht  $-{\rm j} · 1 \text{ V}$:

$$S(f) = 1\,{\rm V} \cdot \big[ {\rm j}\cdot \delta ( f - f_{30} )-{\rm j} \cdot \delta ( f + f_{30} )+ {\rm j} \cdot \delta ( f - f_{50} )-{\rm j} \cdot \delta ( f + f_{50} )\big] \hspace{0.05cm}.$$

(2)  Die Fourierrücktransformation von  $S(f)$  führt mit  $('"`UNIQ-MathJax19-QINU`"' s(t) = -2\,{\rm V} \cdot \sin(\omega_{\rm 30} t )-2\,{\rm V} \cdot \sin(\omega_{\rm 50} t )\hspace{0.05cm}.'"`UNIQ-MathJax20-QINU`"'s(t) = q(t) \cdot z(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} t + \phi_{\rm N})\cdot \cos(\omega_{\rm T} t + \phi_{\rm T})'"`UNIQ-MathJax21-QINU`"'\Rightarrow \hspace{0.5cm} s(t) = \frac{A_{\rm N}}{2} \cdot \left[ \cos\left((\omega_{\rm T} +\omega_{\rm N})\cdot t + \phi_{\rm T}+ \phi_{\rm N}\right) + \cos\left((\omega_{\rm T} -\omega_{\rm N})\cdot t + \phi_{\rm T}- \phi_{\rm N}\right) \right] \hspace{0.05cm}.'"`UNIQ-MathJax22-QINU`"'\cos(\omega_{\rm 30} \cdot t + \phi_{\rm T}- \phi_{\rm N}) = -\sin(\omega_{\rm 30} \cdot t )\hspace{0.05cm},'"`UNIQ-MathJax23-QINU`"'\cos(\omega_{\rm 50} \cdot t + \phi_{\rm T}+ \phi_{\rm N}) = -\sin(\omega_{\rm 50} \cdot t ) \hspace{0.05cm}.'"`UNIQ-MathJax24-QINU`"'q(t ) = 4\,{\rm V} \cdot \cos (2 \pi \cdot 10\,{\rm kHz} \cdot t) \hspace{0.05cm}, \hspace{1.0cm}z(t) = 1 \cdot \cos (2 \pi \cdot 40\,{\rm kHz} \cdot t + 90^{\circ}) = -\sin (2 \pi \cdot 40\,{\rm kHz} \cdot t )\hspace{0.05cm}.$$