Aufgaben:Aufgabe 2.1: Gruppe, Ring, Körper: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
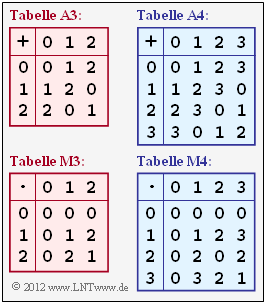
[[Datei:P_ID2490__KC_A_2_1.png|right|Additions– und Multiplikationstabellen für $q = 3$ und $q = 4$]] | [[Datei:P_ID2490__KC_A_2_1.png|right|Additions– und Multiplikationstabellen für $q = 3$ und $q = 4$]] | ||
| + | Im Theorieteil zu diesem Kapitel 2.1 wurden verschiedene algebraische Begriffe definiert. Für das Folgende setzen wir voraus, dass alle Mengen aus jeweils $q$ Elementen bestehen, wobei hier entweder $q = 3$ oder $q = 4$ gelten soll. Dann gilt: | ||
| + | * Eine [[algebraische Gruppe]] ist eine endliche Menge $G = \{0, \, 1, \, \ ... \ , \ q-1\}$ zusammen mit einer zwischen allen Elementen definierten Verknüpfungsvorschrift. Eine additive Gruppe wird mit $(G, \ +)$ bezeichnet, eine multiplikative mit $(G, \ \cdot)$. | ||
| + | |||
| + | * Ein [[algebraischer Ring]] kennzeichnet eine Menge $R = \{0, \, 1, \ ... \ , \ q-1\}$ zusammen mit zwei darin definierten Rechenoperationen, nämlich der Addition („$+$”) und der Multiplikation („$\cdot$”). | ||
| + | |||
| + | * Ein [[algebraischer Körper]] ist ein Ring, bei dem zusätzlich die Division erlaubt ist und stets das Kommutativgesetz erfüllt wird. | ||
| + | |||
| + | |||
| + | Da wir hier ausschließlich endliche Mengen betrachten, ist ein Körper (englisch: <i>Field</i>) gleichzeitig ein Galoisfeld ${\rm GF}(q)$ der Ordnung $q$. | ||
| + | |||
| + | Eine wesentliche Eigenschaft des Galoisfeldes | ||
| + | :$${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.1cm} ... , \hspace{0.1cm}z_{q-1}\}$$ | ||
| + | |||
| + | ist, dass es mindestens ein primitives Element besitzt. Ein Element $z_i ≠ 0$ bezeichnet man als primitiv, wenn die folgende Bedingung erfüllt ist ($k$ ist ganzzahlig): | ||
| + | :$$z_i^k \hspace{0.15cm}{\rm mod}\hspace{0.15cm}q = \left\{ \begin{array}{c} \ne 1\\ | ||
| + | 1 \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm}1 \le k < q-1 | ||
| + | \\ {\rm f\ddot{u}r} \hspace{0.15cm}k = q-1 \\ \end{array} | ||
| + | \hspace{0.35cm} \Rightarrow \hspace{0.35cm} z_i \hspace{0.15cm}{\rm ist \hspace{0.15cm}ein\hspace{0.15cm} primitives \hspace{0.15cm}Element} | ||
| + | \hspace{0.05cm}. $$ | ||
| + | |||
| + | Nur bei einem primitiven Element $z_i$ ergeben sich durch die Rechenoparation $z_i^k$ (mit $k = 1, \, 2, \, 3, \, ...)$ alle Elemente des Galoisfeldes mit Ausnahme des Nullelementes $z_0 = 0$. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe behandelt das Themengebiet des Kapitels [[ | ||
Version vom 14. Dezember 2017, 17:03 Uhr
Im Theorieteil zu diesem Kapitel 2.1 wurden verschiedene algebraische Begriffe definiert. Für das Folgende setzen wir voraus, dass alle Mengen aus jeweils $q$ Elementen bestehen, wobei hier entweder $q = 3$ oder $q = 4$ gelten soll. Dann gilt:
- Eine Algebraische Gruppe ist eine endliche Menge $G = \{0, \, 1, \, \ ... \ , \ q-1\}$ zusammen mit einer zwischen allen Elementen definierten Verknüpfungsvorschrift. Eine additive Gruppe wird mit $(G, \ +)$ bezeichnet, eine multiplikative mit $(G, \ \cdot)$.
- Ein Algebraischer Ring kennzeichnet eine Menge $R = \{0, \, 1, \ ... \ , \ q-1\}$ zusammen mit zwei darin definierten Rechenoperationen, nämlich der Addition („$+$”) und der Multiplikation („$\cdot$”).
- Ein Algebraischer Körper ist ein Ring, bei dem zusätzlich die Division erlaubt ist und stets das Kommutativgesetz erfüllt wird.
Da wir hier ausschließlich endliche Mengen betrachten, ist ein Körper (englisch: Field) gleichzeitig ein Galoisfeld ${\rm GF}(q)$ der Ordnung $q$.
Eine wesentliche Eigenschaft des Galoisfeldes
- $${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.1cm} ... , \hspace{0.1cm}z_{q-1}\}$$
ist, dass es mindestens ein primitives Element besitzt. Ein Element $z_i ≠ 0$ bezeichnet man als primitiv, wenn die folgende Bedingung erfüllt ist ($k$ ist ganzzahlig):
- $$z_i^k \hspace{0.15cm}{\rm mod}\hspace{0.15cm}q = \left\{ \begin{array}{c} \ne 1\\ 1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm}1 \le k < q-1 \\ {\rm f\ddot{u}r} \hspace{0.15cm}k = q-1 \\ \end{array} \hspace{0.35cm} \Rightarrow \hspace{0.35cm} z_i \hspace{0.15cm}{\rm ist \hspace{0.15cm}ein\hspace{0.15cm} primitives \hspace{0.15cm}Element} \hspace{0.05cm}. $$
Nur bei einem primitiven Element $z_i$ ergeben sich durch die Rechenoparation $z_i^k$ (mit $k = 1, \, 2, \, 3, \, ...)$ alle Elemente des Galoisfeldes mit Ausnahme des Nullelementes $z_0 = 0$.
Hinweise:
- Die Aufgabe behandelt das Themengebiet des Kapitels [[
Fragebogen
Musterlösung