Aufgaben:Aufgabe 2.14: Petersen–Algorithmus?: Unterschied zwischen den Versionen
Aus LNTwww
Wael (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Fehlerkorrektur nach Reed–Solomon–Codierung }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Mult…“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Fehlerkorrektur nach Reed–Solomon–Codierung | + | {{quiz-Header|Buchseite=Kanalcodierung/Fehlerkorrektur nach Reed–Solomon–Codierung}} |
| + | [[Datei: P_ID2580__KC_A_2_14_v1.png|right|frame|Schneller Algorithmus zur Decodierung von Reed–Solomon–Codes]] | ||
| + | Im Theorieteil zu [[Kanalcodierung/Fehlerkorrektur_nach_Reed%E2%80%93Solomon%E2%80%93Codierung| Kapitel 2.5]] haben wir die Decodierung von Reed–Solomon–Codes mit dem <i>Petersen–Algorithmus</i> behandelt. | ||
| + | * Dessen Vorteil ist, dass die einzelnen Schritte nachvollziehbar sind. | ||
| + | * Sehr von Nachteil ist aber der immens hohe Decodieraufwand. | ||
| − | + | Schon seit der Erfindung der Reed–Solomon–Codierung im Jahre 1960 beschäftigten sich viele Wissenschaftler und Ingenieure mit der Entwicklung möglichst schneller Algorithmen zur Reed–Solomon–Decodierung, und auch heute ist die <i>Algebraische Decodierung</i> noch ein hochaktuelles Forschungsgebiet. | |
| + | |||
| + | In dieser Aufgabe sollen einige diesbezügliche Begriffe erklärt werden. Auf eine genaue Erklärung dieser Verfahren wurde in LNTwww verzichtet. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe bezieht sich auf das Kapitel [[Kanalcodierung/Fehlerkorrektur_nach_Reed%E2%80%93Solomon%E2%80%93Codierung| Fehlerkorrektur nach Reed–Solomon–Codierung]]. | ||
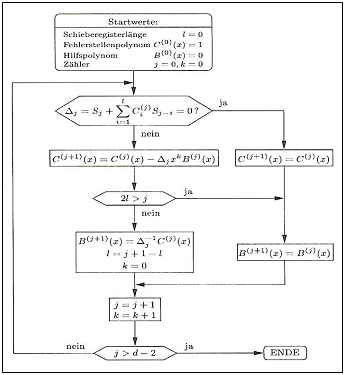
| + | * Die obige Grafik aus [https://intern.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=entitaet&e_id=41798&hyperlink_typ=entitaet_verweis [Bos98]] zeigt das Flussdiagramm eines der bekanntesten Verfahren zur Decodierung von Reed–Solomon–Codes. Um welchen Algorithmus es sich dabei handelt, wird in der Musterlösung zu dieser Aufgabe genannt. | ||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Multiple-Choice | + | {Multiple-Choice |
|type="[]"} | |type="[]"} | ||
| − | + | + correct | |
| − | + | + | - false |
| − | |||
{Input-Box Frage | {Input-Box Frage | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $xyz \ = \ ${ 5.4 3% } $ab$ |
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' |
| − | '''2 | + | '''(2)''' |
| − | '''3 | + | '''(3)''' |
| − | '''4 | + | '''(4)''' |
| − | '''5 | + | '''(5)''' |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Kanalcodierung|^2.5 Fehlerkorrektur nach Reed–Solomon–Codierung | + | [[Category:Aufgaben zu Kanalcodierung|^2.5 Fehlerkorrektur nach Reed–Solomon–Codierung^]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | ^]] | ||
Version vom 18. Dezember 2017, 16:49 Uhr
Im Theorieteil zu Kapitel 2.5 haben wir die Decodierung von Reed–Solomon–Codes mit dem Petersen–Algorithmus behandelt.
- Dessen Vorteil ist, dass die einzelnen Schritte nachvollziehbar sind.
- Sehr von Nachteil ist aber der immens hohe Decodieraufwand.
Schon seit der Erfindung der Reed–Solomon–Codierung im Jahre 1960 beschäftigten sich viele Wissenschaftler und Ingenieure mit der Entwicklung möglichst schneller Algorithmen zur Reed–Solomon–Decodierung, und auch heute ist die Algebraische Decodierung noch ein hochaktuelles Forschungsgebiet.
In dieser Aufgabe sollen einige diesbezügliche Begriffe erklärt werden. Auf eine genaue Erklärung dieser Verfahren wurde in LNTwww verzichtet.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Fehlerkorrektur nach Reed–Solomon–Codierung.
- Die obige Grafik aus [Bos98] zeigt das Flussdiagramm eines der bekanntesten Verfahren zur Decodierung von Reed–Solomon–Codes. Um welchen Algorithmus es sich dabei handelt, wird in der Musterlösung zu dieser Aufgabe genannt.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)