Aufgaben:Aufgabe 2.13: Decodierung beim RSC (7, 3, 5) zur Basis 8: Unterschied zwischen den Versionen
| Zeile 73: | Zeile 73: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 2</u>: | + | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 2</u>: |
| − | *Der ${\rm RSC} \, (7, \, 3, \, 5)_8$ kann bis zu $t = 2$ Symbolfehler korrigieren. | + | *Der ${\rm RSC} \, (7, \, 3, \, 5)_8$ kann bis zu $t = 2$ Symbolfehler korrigieren. |
| − | *Die tatsächliche Symbolfehleranzahl $r$ darf nicht größer sein. | + | |
| + | *Die tatsächliche Symbolfehleranzahl $r$ darf nicht größer sein. | ||
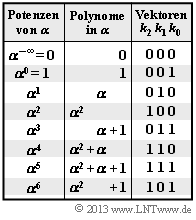
| − | [[Datei:P_ID2562__KC_T_2_5_Darstellung.png|right|frame|Umrechnungstabellen für | + | [[Datei:P_ID2562__KC_T_2_5_Darstellung.png|right|frame|Umrechnungstabellen für $\rm GF(2^3)$]] |
| − | '''(2)''' Unter der Annahme $r = 1$ lauten die $n-k-1$ Bestimmungsgleichungen | + | '''(2)''' Unter der Annahme $r = 1$ lauten die $n-k-1$ Bestimmungsgleichungen $\lambda_0$ gemäß ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$: |
:$$\lambda_0 \cdot 0 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} 1 = 0 \hspace{0.75cm} \Rightarrow \hspace{0.3cm} \lambda_0 \hspace{0.15cm} {\rm unbestimmt} \hspace{0.05cm},$$ | :$$\lambda_0 \cdot 0 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} 1 = 0 \hspace{0.75cm} \Rightarrow \hspace{0.3cm} \lambda_0 \hspace{0.15cm} {\rm unbestimmt} \hspace{0.05cm},$$ | ||
:$$\lambda_0 \cdot 1 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \alpha^5 = 0 \hspace{0.55cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^5 \hspace{0.05cm},$$ | :$$\lambda_0 \cdot 1 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \alpha^5 = 0 \hspace{0.55cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^5 \hspace{0.05cm},$$ | ||
:$$\lambda_0 \cdot \alpha^5 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \alpha^2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{-3} = \alpha^4 \hspace{0.05cm}.$$ | :$$\lambda_0 \cdot \alpha^5 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \alpha^2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{-3} = \alpha^4 \hspace{0.05cm}.$$ | ||
| − | *Die Annahme $r = 1$ wäre nur dann gerechtfertigt, wenn sich aus allen diesen drei Gleichungen der gleiche $\lambda_0$–Wert ergäbe. | + | *Die Annahme $r = 1$ wäre nur dann gerechtfertigt, wenn sich aus allen diesen drei Gleichungen der gleiche $\lambda_0$–Wert ergäbe. |
| + | |||
*Dies ist hier nicht der Fall ⇒ Antwort <u>NEIN</u>. | *Dies ist hier nicht der Fall ⇒ Antwort <u>NEIN</u>. | ||
| − | '''(3)''' Geht man von der Belegrung für $r = 2$ aus, so erhält man zwei Bestimmungsgleichungen für $\lambda_0$ und $\lambda_1$: | + | '''(3)''' Geht man von der Belegrung für $r = 2$ aus, so erhält man zwei Bestimmungsgleichungen für $\lambda_0$ und $\lambda_1$: |
:$$\lambda_0 \cdot 0 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \lambda_1 \cdot 1 +\alpha^5 = 0 \hspace{0.38cm} \Rightarrow \hspace{0.3cm} \lambda_1 = \alpha^5 \hspace{0.05cm},$$ | :$$\lambda_0 \cdot 0 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \lambda_1 \cdot 1 +\alpha^5 = 0 \hspace{0.38cm} \Rightarrow \hspace{0.3cm} \lambda_1 = \alpha^5 \hspace{0.05cm},$$ | ||
:$$\lambda_0 \cdot 1 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \lambda_1 \cdot \alpha^5 +\alpha^2 = 0 \hspace{0.15cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{5+5} +\alpha^2 = \alpha^{3} +\alpha^2 =\alpha^{5} \hspace{0.05cm}.$$ | :$$\lambda_0 \cdot 1 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \lambda_1 \cdot \alpha^5 +\alpha^2 = 0 \hspace{0.15cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{5+5} +\alpha^2 = \alpha^{3} +\alpha^2 =\alpha^{5} \hspace{0.05cm}.$$ | ||
| − | *Das Gleichungssystem lässt sich unter der Annahme $r = 2$ lösen ⇒ Antwort <u>JA</u>. | + | *Das Gleichungssystem lässt sich unter der Annahme $r = 2$ lösen ⇒ Antwort <u>JA</u>. |
| − | *Die hier gewonnenen Ergebnisse $\lambda_0 = \lambda_1 = \alpha^5$ werden in der nächsten Teilaufgabe verarbeitet. | + | |
| + | *Die hier gewonnenen Ergebnisse $\lambda_0 = \lambda_1 = \alpha^5$ werden in der nächsten Teilaufgabe verarbeitet. | ||
| − | '''(4)''' Mit dem Ergebnis $\lambda_0 = \lambda_1 = \alpha^5$ lautet das | + | '''(4)''' Mit dem Ergebnis $\lambda_0 = \lambda_1 = \alpha^5$ lautet das "Error Locator Polynom" (hier die Schlüsselgleichung): |
:$${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + {\it \lambda}_1 \cdot x + x^2 \big ) | :$${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + {\it \lambda}_1 \cdot x + x^2 \big ) | ||
=x \cdot \big (\alpha^5 + \alpha^5 \cdot x + x^2 )\hspace{0.05cm}.$$ | =x \cdot \big (\alpha^5 + \alpha^5 \cdot x + x^2 )\hspace{0.05cm}.$$ | ||
| − | *Diese Funktion weist Nullstellen für $x = \alpha^2$ und $x = \alpha^3$ auf: | + | *Diese Funktion weist Nullstellen für $x = \alpha^2$ und $x = \alpha^3$ auf: |
:$${\it \Lambda}(x = \alpha^2 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^2 \cdot \big ( \alpha^5 + \alpha^7 + \alpha^4 \big ) = \alpha^2 \cdot \big ( \alpha^5 + 1 + \alpha^4 \big )= 0\hspace{0.05cm},$$ | :$${\it \Lambda}(x = \alpha^2 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^2 \cdot \big ( \alpha^5 + \alpha^7 + \alpha^4 \big ) = \alpha^2 \cdot \big ( \alpha^5 + 1 + \alpha^4 \big )= 0\hspace{0.05cm},$$ | ||
:$${\it \Lambda}(x = \alpha^3 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 \cdot \big ( \alpha^5 + \alpha^8 + \alpha^6 \big ) = \alpha^3 \cdot \big ( \alpha^5 + \alpha + \alpha^6 \big )= 0\hspace{0.05cm}.$$ | :$${\it \Lambda}(x = \alpha^3 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 \cdot \big ( \alpha^5 + \alpha^8 + \alpha^6 \big ) = \alpha^3 \cdot \big ( \alpha^5 + \alpha + \alpha^6 \big )= 0\hspace{0.05cm}.$$ | ||
| − | *Verfälscht sind folglich die Symbole an den Positionen 2 und 3 ⇒ <u>Lösungsvorschläge 3 und 4</u>. | + | *Verfälscht sind folglich die Symbole an den Positionen '''2''' und '''3''' ⇒ <u>Lösungsvorschläge 3 und 4</u>. |
| − | '''(5)''' Nach dem Ergebnis der Teilaufgabe '''(4)''' kommen nur noch die beiden letzten Lösungsvorschläge in Frage: | + | '''(5)''' Nach dem Ergebnis der Teilaufgabe '''(4)''' kommen nur noch die beiden letzten Lösungsvorschläge in Frage: |
:$$\underline{e} = (0, \, 0, \, e_2, \, e_3, \, 0, \, 0, \, 0).$$ | :$$\underline{e} = (0, \, 0, \, e_2, \, e_3, \, 0, \, 0, \, 0).$$ | ||
| − | *Der Ansatz lautet deshalb entsprechend $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}$: | + | *Der Ansatz lautet deshalb entsprechend $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}$: |
:$$(0, 0, e_2, e_3, 0, 0, 0) \cdot | :$$(0, 0, e_2, e_3, 0, 0, 0) \cdot | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Zeile 131: | Zeile 134: | ||
\hspace{0.6cm} e_2 \cdot \alpha^{1} + e_6 \cdot \alpha^{5} = \alpha^{2} \hspace{0.05cm}. $$ | \hspace{0.6cm} e_2 \cdot \alpha^{1} + e_6 \cdot \alpha^{5} = \alpha^{2} \hspace{0.05cm}. $$ | ||
| − | *Alle vier Gleichungen werden mit $e_2 = 1$ sowie $e_3 = \alpha^6$ erfüllt ⇒ <u>Lösungsvorschlag 3</u>: | + | *Alle vier Gleichungen werden mit $e_2 = 1$ sowie $e_3 = \alpha^6$ erfüllt ⇒ <u>Lösungsvorschlag 3</u>: |
:$$\underline {e} = (0, \hspace{0.05cm}0, \hspace{0.05cm}1, \hspace{0.05cm}\alpha^6, \hspace{0.05cm}0, \hspace{0.05cm}0, \hspace{0.05cm}0) $$ | :$$\underline {e} = (0, \hspace{0.05cm}0, \hspace{0.05cm}1, \hspace{0.05cm}\alpha^6, \hspace{0.05cm}0, \hspace{0.05cm}0, \hspace{0.05cm}0) $$ | ||
| − | *Mit $\alpha + 1 = \alpha^3$ und $\alpha^5 + \alpha^6 = \alpha$ kommt man vom gegebenen Empfangswort $\underline{y} = (\alpha^2, \, \alpha^3, \, \alpha, \, \alpha^5, \, \alpha^4, \, \alpha^2, \, 1)$ zum Decodierergebnis | + | *Mit $\alpha + 1 = \alpha^3$ und $\alpha^5 + \alpha^6 = \alpha$ kommt man vom gegebenen Empfangswort $\underline{y} = (\alpha^2, \, \alpha^3, \, \alpha, \, \alpha^5, \, \alpha^4, \, \alpha^2, \, 1)$ zum Decodierergebnis |
:$$\underline {z} = (\alpha^2, \hspace{0.05cm}\alpha^3, \hspace{0.05cm}\alpha^3, \hspace{0.05cm}\alpha, \hspace{0.05cm}\alpha^4, \hspace{0.05cm}\alpha^2, \hspace{0.05cm}1) | :$$\underline {z} = (\alpha^2, \hspace{0.05cm}\alpha^3, \hspace{0.05cm}\alpha^3, \hspace{0.05cm}\alpha, \hspace{0.05cm}\alpha^4, \hspace{0.05cm}\alpha^2, \hspace{0.05cm}1) | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | *In der [[Aufgaben:Aufgabe_2.07:_Reed–Solomon–Code_(7,_3,_5)_zur_Basis_8|Aufgabe 2.7]] wurde gezeigt, dass dies ein zulässiges Codewort des ${\rm RSC} \, (7, \, 3, \, 5)_8$ ist. | + | *In der [[Aufgaben:Aufgabe_2.07:_Reed–Solomon–Code_(7,_3,_5)_zur_Basis_8|"Aufgabe 2.7"]] wurde gezeigt, dass dies ein zulässiges Codewort des ${\rm RSC} \, (7, \, 3, \, 5)_8$ ist. |
| − | *Das zugehörige Informationswort lautet $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$. | + | |
| + | *Das zugehörige Informationswort lautet $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 31. Oktober 2022, 14:55 Uhr
In der "Aufgabe 2.12" haben wir den so genannten Petersen–Algorithmus zur Fehlerkorrektur bzw. zur Decodierung des Reed–Solomon–Codes $(7, \, 4, \, 4)_8$ angewendet, der aufgrund der Minimaldistanz $d_{\rm min} = 4$ allerdings nur einen Symbolfehler korrigieren kann $(t = 1)$.
In dieser Aufgabe betrachten wir nun den ${\rm RSC} \, (7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5 \ \Rightarrow \ t = 2$, dessen Prüfmatrix wie folgt lautet:
- $${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2} & \alpha^{6} & \alpha^{3} \end{pmatrix} .$$
Für das betrachtete Empfangswort $\underline{y} = (\alpha^2, \, \alpha^3, \, \alpha, \, \alpha^5, \, \alpha^4, \, \alpha^2, \, 1)$ ergibt sich hier das Syndrom
- $$\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T} = (0, \, 1, \, \alpha^5, \, \alpha^2).$$
Die weitere Vorgehensweise bei der Decodierung geschieht entsprechend den folgenden Theorieseiten:
- Schritt $\rm (B)$: Aufstellen & Auswerten des ELP–Koeffizientenvektors; "ELP" steht für Error Locator Polynom.
- Schritt $\rm (B)$: Lokalisierung der Fehlerstellen,
- Schritt $\rm (D)$: Abschließende Fehlerkorrektur.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Fehlerkorrektur nach Reed–Solomon–Codierung".
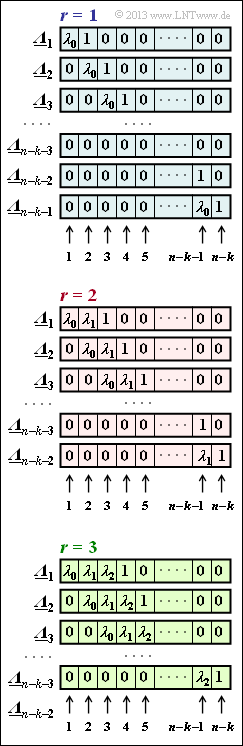
- In obiger Grafik sehen Sie die Belegungen der "ELP–Koeffizienten" ${\it \underline{\Lambda}}_l$ unter der Annahme, dass es im Empfangswort $r = 1, \ r = 2$ bzw. $r = 3$ Symbolfehler gibt.
Fragebogen
Musterlösung
- Der ${\rm RSC} \, (7, \, 3, \, 5)_8$ kann bis zu $t = 2$ Symbolfehler korrigieren.
- Die tatsächliche Symbolfehleranzahl $r$ darf nicht größer sein.
(2) Unter der Annahme $r = 1$ lauten die $n-k-1$ Bestimmungsgleichungen $\lambda_0$ gemäß ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$:
- $$\lambda_0 \cdot 0 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} 1 = 0 \hspace{0.75cm} \Rightarrow \hspace{0.3cm} \lambda_0 \hspace{0.15cm} {\rm unbestimmt} \hspace{0.05cm},$$
- $$\lambda_0 \cdot 1 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \alpha^5 = 0 \hspace{0.55cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^5 \hspace{0.05cm},$$
- $$\lambda_0 \cdot \alpha^5 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \alpha^2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{-3} = \alpha^4 \hspace{0.05cm}.$$
- Die Annahme $r = 1$ wäre nur dann gerechtfertigt, wenn sich aus allen diesen drei Gleichungen der gleiche $\lambda_0$–Wert ergäbe.
- Dies ist hier nicht der Fall ⇒ Antwort NEIN.
(3) Geht man von der Belegrung für $r = 2$ aus, so erhält man zwei Bestimmungsgleichungen für $\lambda_0$ und $\lambda_1$:
- $$\lambda_0 \cdot 0 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \lambda_1 \cdot 1 +\alpha^5 = 0 \hspace{0.38cm} \Rightarrow \hspace{0.3cm} \lambda_1 = \alpha^5 \hspace{0.05cm},$$
- $$\lambda_0 \cdot 1 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \lambda_1 \cdot \alpha^5 +\alpha^2 = 0 \hspace{0.15cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{5+5} +\alpha^2 = \alpha^{3} +\alpha^2 =\alpha^{5} \hspace{0.05cm}.$$
- Das Gleichungssystem lässt sich unter der Annahme $r = 2$ lösen ⇒ Antwort JA.
- Die hier gewonnenen Ergebnisse $\lambda_0 = \lambda_1 = \alpha^5$ werden in der nächsten Teilaufgabe verarbeitet.
(4) Mit dem Ergebnis $\lambda_0 = \lambda_1 = \alpha^5$ lautet das "Error Locator Polynom" (hier die Schlüsselgleichung):
- $${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + {\it \lambda}_1 \cdot x + x^2 \big ) =x \cdot \big (\alpha^5 + \alpha^5 \cdot x + x^2 )\hspace{0.05cm}.$$
- Diese Funktion weist Nullstellen für $x = \alpha^2$ und $x = \alpha^3$ auf:
- $${\it \Lambda}(x = \alpha^2 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^2 \cdot \big ( \alpha^5 + \alpha^7 + \alpha^4 \big ) = \alpha^2 \cdot \big ( \alpha^5 + 1 + \alpha^4 \big )= 0\hspace{0.05cm},$$
- $${\it \Lambda}(x = \alpha^3 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 \cdot \big ( \alpha^5 + \alpha^8 + \alpha^6 \big ) = \alpha^3 \cdot \big ( \alpha^5 + \alpha + \alpha^6 \big )= 0\hspace{0.05cm}.$$
- Verfälscht sind folglich die Symbole an den Positionen 2 und 3 ⇒ Lösungsvorschläge 3 und 4.
(5) Nach dem Ergebnis der Teilaufgabe (4) kommen nur noch die beiden letzten Lösungsvorschläge in Frage:
- $$\underline{e} = (0, \, 0, \, e_2, \, e_3, \, 0, \, 0, \, 0).$$
- Der Ansatz lautet deshalb entsprechend $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}$:
- $$(0, 0, e_2, e_3, 0, 0, 0) \cdot \begin{pmatrix} 1 & 1 & 1 & 1\\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^5\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^2\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^6\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^3 \end{pmatrix} \hspace{0.15cm}\stackrel{!}{=} \hspace{0.15cm} (0, 1, \alpha^5, \alpha^2) \hspace{0.05cm}. $$
- $$\Rightarrow \hspace{0.3cm} e_2 \cdot \alpha^{2} \hspace{-0.15cm} \ + \ \hspace{-0.15cm} e_3 \cdot \alpha^{3} = 0 \hspace{0.05cm}, \hspace{0.8cm} e_2 \cdot \alpha^{4} + e_6 \cdot \alpha^{3} = 1\hspace{0.05cm},\hspace{0.8cm} e_2 \cdot \alpha^{6} \hspace{-0.15cm} \ + \ \hspace{-0.15cm} e_3 \cdot \alpha^{2} = \alpha^{5} \hspace{0.05cm}, \hspace{0.6cm} e_2 \cdot \alpha^{1} + e_6 \cdot \alpha^{5} = \alpha^{2} \hspace{0.05cm}. $$
- Alle vier Gleichungen werden mit $e_2 = 1$ sowie $e_3 = \alpha^6$ erfüllt ⇒ Lösungsvorschlag 3:
- $$\underline {e} = (0, \hspace{0.05cm}0, \hspace{0.05cm}1, \hspace{0.05cm}\alpha^6, \hspace{0.05cm}0, \hspace{0.05cm}0, \hspace{0.05cm}0) $$
- Mit $\alpha + 1 = \alpha^3$ und $\alpha^5 + \alpha^6 = \alpha$ kommt man vom gegebenen Empfangswort $\underline{y} = (\alpha^2, \, \alpha^3, \, \alpha, \, \alpha^5, \, \alpha^4, \, \alpha^2, \, 1)$ zum Decodierergebnis
- $$\underline {z} = (\alpha^2, \hspace{0.05cm}\alpha^3, \hspace{0.05cm}\alpha^3, \hspace{0.05cm}\alpha, \hspace{0.05cm}\alpha^4, \hspace{0.05cm}\alpha^2, \hspace{0.05cm}1) \hspace{0.05cm}. $$
- In der "Aufgabe 2.7" wurde gezeigt, dass dies ein zulässiges Codewort des ${\rm RSC} \, (7, \, 3, \, 5)_8$ ist.
- Das zugehörige Informationswort lautet $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$.