Aufgaben:Aufgabe 2.13: Decodierung beim RSC (7, 3, 5) zur Basis 8: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
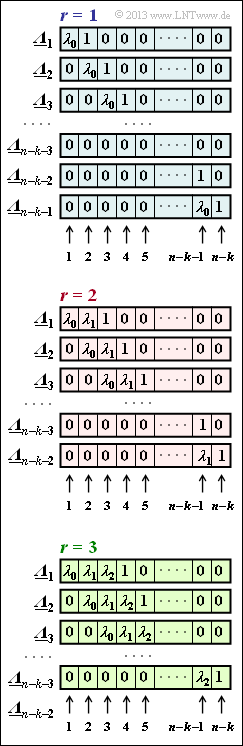
[[Datei:P_ID2561__KC_A_2_12.png|right|frame|ELP–Belegungsschemata für $r = 1, \ r = 2, \ r = 3$]] | [[Datei:P_ID2561__KC_A_2_12.png|right|frame|ELP–Belegungsschemata für $r = 1, \ r = 2, \ r = 3$]] | ||
| + | In der [[Aufgabe A2.12]] haben wir den so genannten Petersen–Algorithmus zur Fehlerkorrektur bzw. zur Decodierung des Reed–Solomon–Codes $(7, \, 4, \, 4)_8$ angewendet, der aufgrund der Minimaldistanz $d_{\rm min} = 4$ nur einen Symbolfehler korrigieren kann $(t = 1)$. | ||
| + | In dieser Aufgabe betrachten wir nun den ${\rm RSC} \, (7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5 \ \Rightarrow \ t = 2$, dessen Prüfmatrix wie folgt lautet: | ||
| + | :$${ \boldsymbol{\rm H}} = | ||
| + | \begin{pmatrix} | ||
| + | 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ | ||
| + | 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ | ||
| + | 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4}\\ | ||
| + | 1 & \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2} & \alpha^{6} & \alpha^{3} | ||
| + | \end{pmatrix} .$$ | ||
| + | |||
| + | Für das betrachtete Empfangswort $\underline{y} = (\alpha^2, \, \alpha^3, \, \alpha, \, \alpha^5, \, \alpha^4, \, \alpha^2, \, 1)$ ergibt sich hier das Syndrom zu $\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T} = (0, \, 1, \, \alpha^5, \, \alpha^2)$. | ||
| + | |||
| + | Die weitere Vorgehensweise bei der Decodierung geschieht entsprechend den folgenden Theorieseiten: | ||
| + | * Schritt (B): [[Bestimmung der Symbolfehleranzahl]], | ||
| + | * Schritt(C): [[Lokalisierung der Fehlerpositionen]], | ||
| + | * Schritt (D): [[Ermittlung der Fehlerwerte]]. | ||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | * | ||
Version vom 18. Dezember 2017, 15:46 Uhr
In der Aufgabe A2.12 haben wir den so genannten Petersen–Algorithmus zur Fehlerkorrektur bzw. zur Decodierung des Reed–Solomon–Codes $(7, \, 4, \, 4)_8$ angewendet, der aufgrund der Minimaldistanz $d_{\rm min} = 4$ nur einen Symbolfehler korrigieren kann $(t = 1)$.
In dieser Aufgabe betrachten wir nun den ${\rm RSC} \, (7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5 \ \Rightarrow \ t = 2$, dessen Prüfmatrix wie folgt lautet:
- $${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2} & \alpha^{6} & \alpha^{3} \end{pmatrix} .$$
Für das betrachtete Empfangswort $\underline{y} = (\alpha^2, \, \alpha^3, \, \alpha, \, \alpha^5, \, \alpha^4, \, \alpha^2, \, 1)$ ergibt sich hier das Syndrom zu $\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T} = (0, \, 1, \, \alpha^5, \, \alpha^2)$.
Die weitere Vorgehensweise bei der Decodierung geschieht entsprechend den folgenden Theorieseiten:
- Schritt (B): Bestimmung der Symbolfehleranzahl,
- Schritt(C): Lokalisierung der Fehlerpositionen,
- Schritt (D): Ermittlung der Fehlerwerte.
Hinweise:
Fragebogen
Musterlösung