Aufgaben:Aufgabe 2.11Z: Erasure–Kanal für Symbole: Unterschied zwischen den Versionen
K (Textersetzung - „* Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Zeile 2: | Zeile 2: | ||
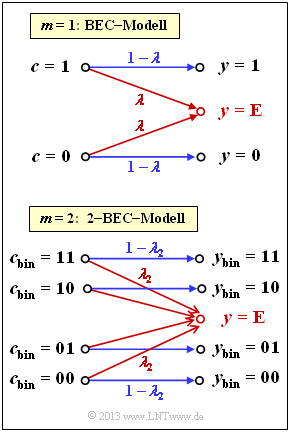
[[Datei:P_ID2543__KC_Z_2_11.png|right|frame|Auslöschungskanal für Symbole: $m$–BEC]] | [[Datei:P_ID2543__KC_Z_2_11.png|right|frame|Auslöschungskanal für Symbole: $m$–BEC]] | ||
| − | Das Kanalmodell [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|Binary Erasure Channel]] (BEC) beschreibt einen Auslöschungskanal auf Bitebene: | + | Das Kanalmodell [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|Binary Erasure Channel]] (BEC) beschreibt einen Auslöschungskanal auf Bitebene: |
| − | *Ein Binärsymbol $0$ bzw. $1$ wird mit der Wahrscheinlichkeit $1 - \lambda$ richtig übertragen und mit der Wahrscheinlichkeit $\lambda$ als Auslöschung $\rm E$ (<i>Erasure</i>) markiert. | + | *Ein Binärsymbol $0$ bzw. $1$ wird mit der Wahrscheinlichkeit $1 - \lambda$ richtig übertragen und mit der Wahrscheinlichkeit $\lambda$ als Auslöschung $\rm E$ (<i>Erasure</i> ) markiert. |
| − | *Im Gegensatz zum [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC| Binary Symmetric Channel]] (BSC) kann es hier nicht zu Verfälschungen $(0 → 1, \ 1 → 0)$ kommen. | + | *Im Gegensatz zum [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC| Binary Symmetric Channel]] (BSC) kann es hier nicht zu Verfälschungen $(0 → 1, \ 1 → 0)$ kommen. |
| + | |||
| + | |||
| + | Ein Reed–Solomon–Code basiert auf einem Galoisfeld ${\rm GF}(2^m)$ mit ganzzahligem $m$. Somit lässt sich jedes Codesymbol $c$ durch $m$ Bit darstellen. Will man hier das BEC–Modell anwenden, so muss man dieses zum $m\text{-BEC}$-Modell modifizieren, wie es in der unteren Grafik für $m = 2$ gezeigt ist: | ||
| + | |||
| + | *Alle Codesymbole – in Binärdarstellung $00, \ 01, \ 10, \ 11$ – werden mit Wahrscheinlichkeit $1 - \lambda_2$ richtig übertragen. | ||
| + | *Damit beträgt die Wahrscheinlichkeit für ein ausgelöschtes Symbol $\lambda_2$. | ||
| + | *Zu beachten ist, dass bereits ein einziges ausgelöschtes Bit zum ausgelöschten Empfangssymbol $y = \rm E$ führt. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 17: | Zeile 20: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Reed%E2%80%93Solomon%E2%80%93Decodierung_beim_Ausl%C3%B6schungskanal| Reed–Solomon–Decodierung beim Auslöschungskanal]]. | + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Reed%E2%80%93Solomon%E2%80%93Decodierung_beim_Ausl%C3%B6schungskanal| Reed–Solomon–Decodierung beim Auslöschungskanal]]. |
| − | * Bei einem auf ${\rm GF}(2^m)$ basierenden Code ist das skizzierte 2–BEC–Modell zum $m$–BEC zu erweitern. Die Auslöschungswahrscheinlichkeit dieses Modell wird dann mit $\lambda_m$ bezeichnet. | + | * Bei einem auf ${\rm GF}(2^m)$ basierenden Code ist das skizzierte $2$–BEC–Modell zum $m$–BEC zu erweitern. |
| − | * Für die ersten Teilaufgaben gelte für die Auslöschungswahrscheinlichkeit des Grundmodells gemäß der oberen Grafik stets $\lambda = 0.2$. | + | *Die Auslöschungswahrscheinlichkeit dieses Modell wird dann mit $\lambda_m$ bezeichnet. |
| + | * Für die ersten Teilaufgaben gelte für die Auslöschungswahrscheinlichkeit des Grundmodells gemäß der oberen Grafik stets $\lambda = 0.2$. | ||
| Zeile 26: | Zeile 30: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Es gelte $\lambda = 0.2$. Mit welchen Wahrscheinlichkeiten treten beim BEC–Grundmodell die möglichen Empfangswerte auf? | + | {Es gelte $\lambda = 0.2$. Mit welchen Wahrscheinlichkeiten treten beim BEC–Grundmodell die möglichen Empfangswerte auf? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(y = 0) \ = \ ${ 40 3% } $\ \%$ | ${\rm Pr}(y = 0) \ = \ ${ 40 3% } $\ \%$ | ||
| Zeile 32: | Zeile 36: | ||
${\rm Pr}(y = {\rm 1}) \ = \ ${ 40 3% } $\ \%$ | ${\rm Pr}(y = {\rm 1}) \ = \ ${ 40 3% } $\ \%$ | ||
| − | {Wie groß ist die Auslöschungswahrscheinlichkeit $\lambda_2$ auf Symbolebene (2–BEC–Modell), wenn der RS–Code auf $\rm GF(2^2)$ basiert $(\lambda = 0.2)$? | + | {Wie groß ist die Auslöschungswahrscheinlichkeit $\lambda_2$ auf Symbolebene $(2$–BEC–Modell$)$, wenn der RS–Code auf $\rm GF(2^2)$ basiert $(\lambda = 0.2)$? |
|type="{}"} | |type="{}"} | ||
$\lambda_2 \ = \ ${ 36 3% } $\ \%$ | $\lambda_2 \ = \ ${ 36 3% } $\ \%$ | ||
| − | {Wie groß ist die Auslöschungswahrscheinlichkeit $\lambda_m$, wenn das $m$–BEC–Modell an den $\rm RSC \, (255, \, 223, \, 33)_{256}$ angepasst wird $(\lambda = 0.2)$? | + | {Wie groß ist die Auslöschungswahrscheinlichkeit $\lambda_m$, wenn das $m$–BEC–Modell an den $\rm RSC \, (255, \, 223, \, 33)_{256}$ angepasst wird $(\lambda = 0.2)$? |
|type="{}"} | |type="{}"} | ||
$\lambda_m \ = \ ${ 83.2 3% } $\ \%$ | $\lambda_m \ = \ ${ 83.2 3% } $\ \%$ | ||
| − | {Wie groß darf die Auslöschungswahrscheinlichkeit $\lambda$ beim BEC–Grundmodell maximal sein, damit $\lambda_m ≤ 0.2$ gilt? | + | {Wie groß darf die Auslöschungswahrscheinlichkeit $\lambda$ beim BEC–Grundmodell maximal sein, damit $\lambda_m ≤ 0.2$ gilt? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Max} \ [\lambda] \ = \ ${ 2.75 3% } $\ \%$ | + | ${\rm Max} \ \big[\lambda\big ] \ = \ ${ 2.75 3% } $\ \%$ |
{Mit welcher Wahrscheinlichkeit wird in diesem Fall das „Nullsymbol” empfangen? | {Mit welcher Wahrscheinlichkeit wird in diesem Fall das „Nullsymbol” empfangen? | ||
Version vom 24. Mai 2019, 11:37 Uhr
Das Kanalmodell Binary Erasure Channel (BEC) beschreibt einen Auslöschungskanal auf Bitebene:
- Ein Binärsymbol $0$ bzw. $1$ wird mit der Wahrscheinlichkeit $1 - \lambda$ richtig übertragen und mit der Wahrscheinlichkeit $\lambda$ als Auslöschung $\rm E$ (Erasure ) markiert.
- Im Gegensatz zum Binary Symmetric Channel (BSC) kann es hier nicht zu Verfälschungen $(0 → 1, \ 1 → 0)$ kommen.
Ein Reed–Solomon–Code basiert auf einem Galoisfeld ${\rm GF}(2^m)$ mit ganzzahligem $m$. Somit lässt sich jedes Codesymbol $c$ durch $m$ Bit darstellen. Will man hier das BEC–Modell anwenden, so muss man dieses zum $m\text{-BEC}$-Modell modifizieren, wie es in der unteren Grafik für $m = 2$ gezeigt ist:
- Alle Codesymbole – in Binärdarstellung $00, \ 01, \ 10, \ 11$ – werden mit Wahrscheinlichkeit $1 - \lambda_2$ richtig übertragen.
- Damit beträgt die Wahrscheinlichkeit für ein ausgelöschtes Symbol $\lambda_2$.
- Zu beachten ist, dass bereits ein einziges ausgelöschtes Bit zum ausgelöschten Empfangssymbol $y = \rm E$ führt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Reed–Solomon–Decodierung beim Auslöschungskanal.
- Bei einem auf ${\rm GF}(2^m)$ basierenden Code ist das skizzierte $2$–BEC–Modell zum $m$–BEC zu erweitern.
- Die Auslöschungswahrscheinlichkeit dieses Modell wird dann mit $\lambda_m$ bezeichnet.
- Für die ersten Teilaufgaben gelte für die Auslöschungswahrscheinlichkeit des Grundmodells gemäß der oberen Grafik stets $\lambda = 0.2$.
Fragebogen
Musterlösung
- $$\ {\rm Pr}(y = {\rm E}) = \lambda \ \underline{= 20\%}.$$
Da die Codesymbole $0$ und $1$ gleichwahrscheinlich sind, erhält man für deren Wahrscheinlichkeiten ${\rm Pr}(y = 0) \ \underline{= 40\%}$ und ${\rm Pr}(y = 1) \ \underline{= 40\%}$.
(2) Ohne Einschränkung der Allgemeingültigkeit gehen wir zur Lösung dieser Aufgabe vom Codesymbol $c_{\rm binär} = $ „$00$” aus.
- Entsprechend dem 2–BEC–Modell kann dann das Empfangssymbol $y_{\rm binär}$ entweder „$00$” oder ausgelöscht $(\rm E)$ sein und es gilt:
- $${\rm Pr}(y_{\rm bin} = "00"\hspace{0.05cm} |\hspace{0.05cm} c_{\rm bin} = "00") \hspace{-0.15cm} \ = \ \hspace{-0.15cm} ( 1 - \lambda)^2 = 0.8^2 = 0.64 = 1 - \lambda_2\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 - ( 1 - \lambda)^2 \hspace{0.15cm}\underline{= 36\%}\hspace{0.05cm}. $$
- Hierbei ist vorausgesetzt, dass ein Erasure nur vermieden wird, wenn keines der zwei Bit ausgelöscht wurde.
(3) Der $\rm RSC \, (255, \, 223, \, 33)_{256}$ basiert auf dem Galoisfeld $\rm GF(256) = GF(2^8) \ \Rightarrow \ \it m = \rm 8$. Das Ergebnis der Teilaufgabe (2) muss nun an diesen Fall angepasst werden. Für den $8$–BEC gilt:
- $$1 - \lambda_8 = ( 1 - \lambda)^8 = 0.8^8 \approx 0.168 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_m = \lambda_8 \hspace{0.15cm}\underline{\approx 83.2\%}\hspace{0.05cm}. $$
(4) Aus der Bedingung $\lambda_m ≤ 0.2$ folgt direkt $1 - \lambda_m ≥ 0.8$. Daraus folgt weiter:
- $$( 1 - \lambda)^8 \ge 0.8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1 - \lambda \ge 0.8^{0.125} \approx 0.9725 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\lambda \hspace{0.15cm} \underline{\le 2.75\%}\hspace{0.05cm}.$$
(5) Hier geht man wie folgt vor:
- Mit $\lambda = 0.0275 \ \Rightarrow \ \lambda_m = 0.2$ sind $20\%$ der Empfangssymbole Erasures.
- Die $2^8 = 256$ Empfangssymbole ($00000000$ ... $11111111$) sind alle gleichwahrscheinlich. Daraus folgt:
- $${\rm Pr}(y_{\rm bin} = 00000000) = \hspace{0.1cm}\text{...} \hspace{0.1cm}= {\rm Pr}(y_{\rm bin} = 11111111)= \frac{0.8}{256} \hspace{0.15cm}\underline{= 0.3125\%}\hspace{0.05cm}.$$