Aufgaben:Aufgabe 2.10: Fehlererkennung bei Reed–Solomon: Unterschied zwischen den Versionen
| Zeile 85: | Zeile 85: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die Gleichung zur Beschreibung der Gewichte $W_i$ lautet (die minimale Distanz $d_{\rm min}$ ist hier mit $d$ abgekürzt): | + | '''(1)''' Die Gleichung zur Beschreibung der Gewichte $W_i$ lautet $($die minimale Distanz $d_{\rm min}$ ist hier mit $d$ abgekürzt$)$: |
:$$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$ | :$$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$ | ||
| − | Wegen der minimalen Distanz $d_{\min} = 5$ sind $W_3 \ \underline{= 0}$ und $W_4 \ \underline{= 0}$. Die weiteren Gewichte ergeben sich zu | + | *Wegen der minimalen Distanz $d_{\min} = 5$ sind $W_3 \ \underline{= 0}$ und $W_4 \ \underline{= 0}$. Die weiteren Gewichte ergeben sich zu |
:$$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 | :$$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 | ||
\hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$ | \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$ | ||
| Zeile 98: | Zeile 98: | ||
| − | '''(2)''' Analog zur Teilaufgabe (1) erhält man: | + | '''(2)''' Analog zur Teilaufgabe '''(1)''' erhält man: |
:$$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 | :$$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 | ||
\hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' Die Verfälschungswahrscheinlichkeit eines Symbols ist mit $\varepsilon_{\rm S} = 0.1$ gegeben. | + | '''(3)''' Die Verfälschungswahrscheinlichkeit eines Symbols ist mit $\varepsilon_{\rm S} = 0.1$ gegeben. Dann gilt für die Wahrscheinlichkeit, dass in einem Codewort mit $n = 7$ Codesymbolen |
| − | + | * genau drei Symbole verfälscht werden: | |
| − | |||
| − | * genau | ||
:$$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} | :$$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * genau | + | * genau vier Symbole verfälscht werden: |
:$$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} | :$$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * genau | + | * genau fünf Symbole verfälscht werden: |
:$$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} | :$$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * genau | + | * genau sechs Symbole verfälscht werden: |
:$$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$ | :$$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$ | ||
* alle $n = 7$ Symbole verfälscht werden: | * alle $n = 7$ Symbole verfälscht werden: | ||
:$$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$ | :$$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$ | ||
| − | Beim $\rm RSC \, (7, \, 3, \, 5)_8$ kann das Nullwort durch Symbolfehler in eines von $q^k - 1 = 8^3 - 1 = 511$ anderen Codeworten verfälscht werden. | + | ⇒ Beim $\rm RSC \, (7, \, 3, \, 5)_8$ kann das Nullwort durch Symbolfehler in eines von $q^k - 1 = 8^3 - 1 = 511$ anderen Codeworten verfälscht werden. Damit erhält man mit den Gewichtsfunktionen von Teilaufgabe '''(1)''': |
| − | |||
| − | Damit erhält man mit den Gewichtsfunktionen von Teilaufgabe (1): | ||
:$${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} | :$${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} | ||
\hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$ | \hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$ | ||
| − | Beim $\rm RSC \, (7, \, 5, \, 3)_8$ muss wegen $k = 5$ über $8^5 - 1 = 32767$ Verfälschungswahrscheinlichkeiten gemittelt werden. | + | ⇒ Beim $\rm RSC \, (7, \, 5, \, 3)_8$ muss wegen $k = 5$ über $8^5 - 1 = 32767$ Verfälschungswahrscheinlichkeiten gemittelt werden. Mit $W_3 = 245$ aus Teilaufgabe '''(2)''' und den Gewichten |
| − | + | :$$W_4 = 1224, \ W_5 = 5586, \ W_6 = 12838, \ W_7 = 12873$$ | |
| − | Mit $W_3 = 245$ aus Teilaufgabe (2) und den Gewichten $W_4 = 1224, \ W_5 = 5586, \ W_6 = 12838, \ W_7 = 12873$ gemäß Angabenblatt erhält man hierfür: | + | gemäß Angabenblatt erhält man hierfür: |
:$${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_3 \cdot p_3 + W_4 \cdot p_4 + W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{32767} =\frac {245 \cdot 0.656 \cdot 10^{-3} + \hspace{0.15cm}... \hspace{0.15cm}+ 12873 \cdot 10^{-7}}{32767} | :$${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_3 \cdot p_3 + W_4 \cdot p_4 + W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{32767} =\frac {245 \cdot 0.656 \cdot 10^{-3} + \hspace{0.15cm}... \hspace{0.15cm}+ 12873 \cdot 10^{-7}}{32767} | ||
\hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}. $$ | \hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}. $$ | ||
| + | '''(4)''' Bekannt sei nur $d_{\rm min}$ $($weiter mit $d$ abgekürzt$)$ und damit auch $p_d = \varepsilon_{\rm S}^d \cdot (1 - \varepsilon_{\rm S})^{n-d}$. Dies ist gleichzeitig die gesuchte obere Schranke: | ||
| + | :* ${\rm RSC} \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_5 = \underline{0.81 \cdot 10^{-5}}$, | ||
| − | + | :* ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_3 = \underline{65.6 \cdot 10^{-5}}$. | |
| − | |||
| − | * ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_3 = \underline{65.6 \cdot 10^{-5}}$. | ||
| − | |||
| − | Da das Gewicht $W_d$ als nicht bekannt vorausgesetzt wurde, setzt man dieses auf den maximal möglichen Wert ( | + | *Da das Gewicht $W_d$ als nicht bekannt vorausgesetzt wurde, setzt man dieses auf den maximal möglichen Wert $(W_5 = 511$ bzw. $W_3 = 32767)$, so dass die Vorfaktoren in den Gleichungen zur Teilaufgabe '''(3)''' verschwinden. Nur so ist eine obere Schranke sichergestellt. |
| − | Die obere Schranke liegt in beiden Fällen deutlich über den Ergebnissen der Teilaufgabe (3): | + | *Die obere Schranke liegt in beiden Fällen deutlich über den Ergebnissen der Teilaufgabe '''(3)''': |
| − | * $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ statt $0.263 \cdot 10^{-5}$ (Faktor ca. $3 | + | :* $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ statt $0.263 \cdot 10^{-5}$ $($Faktor ca. $3)$, |
| − | |||
| + | :* $\rm RSC \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} 65.6 \cdot 10^{-5}$ statt $0.942 \cdot 10^{-5}$ (Faktor ca. $70$). | ||
| − | '''(5)''' Mit der Abkürzung $d = d_{\rm min}$ erhält man für die untere Schranke: | + | '''(5)''' Mit der Abkürzung $d = d_{\rm min}$ erhält man für die untere Schranke: |
:$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke})= \frac{W_d \cdot p_d}{q^k -1} | :$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke})= \frac{W_d \cdot p_d}{q^k -1} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * Für den $\rm RSC \, (7, \, 3, \, 5)_8$ liegt wegen $W_d = W_5$ und $p_d = p_5$ die unter Schranke um etwa $11\%$ unterhalb des tatsächlichen Wertes $(0.263 \cdot 10^{-5})$: | + | * Für den $\rm RSC \, (7, \, 3, \, 5)_8$ liegt wegen $W_d = W_5$ und $p_d = p_5$ die unter Schranke um etwa $11\%$ unterhalb des tatsächlichen Wertes $(0.263 \cdot 10^{-5})$: |
:$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{147 \cdot 0.81 \cdot 10^{-5}}{511} | :$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{147 \cdot 0.81 \cdot 10^{-5}}{511} | ||
\hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$ | \hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$ | ||
| − | * Für den $\rm RSC \, (7, \, 5, \, 3)_8$ gilt mit $W_d = W_3$ und $p_d = p_3$ weicht die untere Schranke hier vom tatsächlichen Wert $(0.942 \cdot 10^{-5})$stärker ab, weil bei diesem Code die Beiträge der höheren Gewichte $(W_4, \ W_5, \ W_6, \ W_7)$ in Relation zu $W_3$ relevanter sind: | + | * Für den $\rm RSC \, (7, \, 5, \, 3)_8$ gilt mit $W_d = W_3$ und $p_d = p_3$ weicht die untere Schranke hier vom tatsächlichen Wert $(0.942 \cdot 10^{-5})$ stärker ab, weil bei diesem Code die Beiträge der höheren Gewichte $(W_4, \ W_5, \ W_6, \ W_7)$ in Relation zu $W_3$ relevanter sind: |
:$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{245 \cdot 0.656 \cdot 10^{-3}}{32767} | :$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{245 \cdot 0.656 \cdot 10^{-3}}{32767} | ||
\hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$ | ||
Aktuelle Version vom 11. Oktober 2022, 17:26 Uhr
Bei einem linearen Blockcode können bis zu $e = d_{\rm min} - 1$ Fehler erkannt werden. Bei allen Reed–Solomon–Codes beträgt dabei die minimale Distanz
- $$d_{\rm min} = n-k+1 \hspace{0.05cm}.$$
Man muss folgende Fälle unterscheiden:
- Treten nicht mehr als $e = d_{\rm min} - 1= n - k$ Symbolfehler auf, so wird der Block stets als fehlerhaft erkannt.
- Die Fehlererkennung kann auch bei mehr als $n - k$ Symbolfehlern noch funktionieren, und zwar dann, wenn das Empfangswort kein gültiges Codewort des Reed–Solomon–Codes ist:
- $$\underline {y } \notin C_{\rm RS} = \{ \underline {c}_{\hspace{0.05cm}0}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_i, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_{\hspace{0.05cm}n -1} \} \hspace{0.05cm}. $$
- Ist aber das verfälschte Empfangswort $(\underline{y} \ne \underline{c})$ ein gültiges Codewort $(\underline{y\in C_{\rm RS}})$, so bleibt bei der Decodierung der fehlerhafte Block unentdeckt.
Wir definieren als Blockfehlerwahrscheinlichkeit:
- $${\rm Pr}({\rm Blockfehler}) = {\rm Pr}(\underline {y} \ne \underline {c}) \hspace{0.05cm}.$$
In dieser Aufgabe soll diese Wahrscheinlichkeit für folgende Codes ermittelt werden:
- Reed–Solomon–Code $(7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5$,
- Reed–Solomon–Code $(7, \, 5, \, 3)_8 \ \Rightarrow \ d_{\rm min} = 3$.
Weiterhin soll gelten:
- Jedes Symbol wird mit der Wahrscheinlichkeit $\varepsilon_{\rm S} = 0.1$ in ein anderes Symbol verfälscht und mit der Wahrscheinlichkeit $1 - \varepsilon_{\rm S} = 0.9$ richtig übertragen.
- Für das Distanzspektrum eines Reed–Solomon–Codes der Länge $n$ gilt mit $d = d_{\rm min}$:
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
Daneben sollen zwei Schranken für die Blockfehlerwahrscheinlichkeit betrachtet und bewertet werden:
- Ist allein die minimale Distanz bekannt, so kann man daraus eine obere Schranke ableiten. Die Gewichtsfaktoren $W_i$ sind dabei so zu wählen, dass sicher (das heißt: bei allen Konstellationen) gilt:
- $${\rm Pr}({\rm Obere\hspace{0.15cm} Schranke}) \ge {\rm Pr}({\rm Blockfehler}) \hspace{0.05cm}. $$
- Eine untere Schranke erfordert zusätzlich die Kenntnis der Gewichtsfunktion $W_i$ für $i = d_{\rm min}$. Damit kann folgende Bedingung erfüllt werden:
- $${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) \le {\rm Pr}({\rm Blockfehler}) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Definition und Eigenschaften von Reed–Solomon–Codes".
- Bezug genommen wird insbesondere auf die Seite "Singleton–Schranke und minimale Distanz".
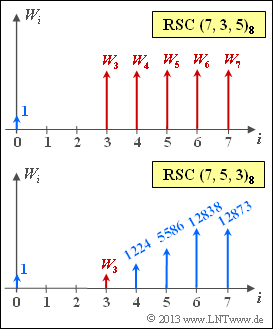
- Zu berechnen sind die in der obigen Grafik rot markierten Gewichte $W_i$.
Fragebogen
Musterlösung
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
- Wegen der minimalen Distanz $d_{\min} = 5$ sind $W_3 \ \underline{= 0}$ und $W_4 \ \underline{= 0}$. Die weiteren Gewichte ergeben sich zu
- $$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$
- $$W_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 6} \cdot \sum_{j = 0}^{1}\hspace{0.15cm}(-1)^j \cdot {6 \choose j} \cdot \big (\hspace{0.03cm}8^{2\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )=7 \cdot \left [ (8^2 - 1) - 6 \cdot (8^1 - 1)\right ] = 7 \cdot (63-42) \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$
- $$W_7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 7} \cdot \sum_{j = 0}^{2}\hspace{0.15cm}(-1)^j \cdot {7 \choose j} \cdot \big (\hspace{0.03cm}8^{3\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )= (8^3 - 1) - 7 \cdot (8^2 - 1) +21 \cdot (8^1 - 1) = 511 - 7 \cdot 63 + 21 \cdot 7 \hspace{0.15cm}\underline {= 217}\hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm}W_0 + W_5 + W_6 + W_7 = 1 + 147 + 147 + 217 = 512 = 8^3 = q^k\hspace{0.05cm}.$$
(2) Analog zur Teilaufgabe (1) erhält man:
- $$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 \hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$
(3) Die Verfälschungswahrscheinlichkeit eines Symbols ist mit $\varepsilon_{\rm S} = 0.1$ gegeben. Dann gilt für die Wahrscheinlichkeit, dass in einem Codewort mit $n = 7$ Codesymbolen
- genau drei Symbole verfälscht werden:
- $$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} \hspace{0.05cm},$$
- genau vier Symbole verfälscht werden:
- $$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} \hspace{0.05cm},$$
- genau fünf Symbole verfälscht werden:
- $$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} \hspace{0.05cm},$$
- genau sechs Symbole verfälscht werden:
- $$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$
- alle $n = 7$ Symbole verfälscht werden:
- $$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$
⇒ Beim $\rm RSC \, (7, \, 3, \, 5)_8$ kann das Nullwort durch Symbolfehler in eines von $q^k - 1 = 8^3 - 1 = 511$ anderen Codeworten verfälscht werden. Damit erhält man mit den Gewichtsfunktionen von Teilaufgabe (1):
- $${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} \hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$
⇒ Beim $\rm RSC \, (7, \, 5, \, 3)_8$ muss wegen $k = 5$ über $8^5 - 1 = 32767$ Verfälschungswahrscheinlichkeiten gemittelt werden. Mit $W_3 = 245$ aus Teilaufgabe (2) und den Gewichten
- $$W_4 = 1224, \ W_5 = 5586, \ W_6 = 12838, \ W_7 = 12873$$
gemäß Angabenblatt erhält man hierfür:
- $${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_3 \cdot p_3 + W_4 \cdot p_4 + W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{32767} =\frac {245 \cdot 0.656 \cdot 10^{-3} + \hspace{0.15cm}... \hspace{0.15cm}+ 12873 \cdot 10^{-7}}{32767} \hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}. $$
(4) Bekannt sei nur $d_{\rm min}$ $($weiter mit $d$ abgekürzt$)$ und damit auch $p_d = \varepsilon_{\rm S}^d \cdot (1 - \varepsilon_{\rm S})^{n-d}$. Dies ist gleichzeitig die gesuchte obere Schranke:
- ${\rm RSC} \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_5 = \underline{0.81 \cdot 10^{-5}}$,
- ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_3 = \underline{65.6 \cdot 10^{-5}}$.
- Da das Gewicht $W_d$ als nicht bekannt vorausgesetzt wurde, setzt man dieses auf den maximal möglichen Wert $(W_5 = 511$ bzw. $W_3 = 32767)$, so dass die Vorfaktoren in den Gleichungen zur Teilaufgabe (3) verschwinden. Nur so ist eine obere Schranke sichergestellt.
- Die obere Schranke liegt in beiden Fällen deutlich über den Ergebnissen der Teilaufgabe (3):
- $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ statt $0.263 \cdot 10^{-5}$ $($Faktor ca. $3)$,
- $\rm RSC \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} 65.6 \cdot 10^{-5}$ statt $0.942 \cdot 10^{-5}$ (Faktor ca. $70$).
(5) Mit der Abkürzung $d = d_{\rm min}$ erhält man für die untere Schranke:
- $${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke})= \frac{W_d \cdot p_d}{q^k -1} \hspace{0.05cm}. $$
- Für den $\rm RSC \, (7, \, 3, \, 5)_8$ liegt wegen $W_d = W_5$ und $p_d = p_5$ die unter Schranke um etwa $11\%$ unterhalb des tatsächlichen Wertes $(0.263 \cdot 10^{-5})$:
- $${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{147 \cdot 0.81 \cdot 10^{-5}}{511} \hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$
- Für den $\rm RSC \, (7, \, 5, \, 3)_8$ gilt mit $W_d = W_3$ und $p_d = p_3$ weicht die untere Schranke hier vom tatsächlichen Wert $(0.942 \cdot 10^{-5})$ stärker ab, weil bei diesem Code die Beiträge der höheren Gewichte $(W_4, \ W_5, \ W_6, \ W_7)$ in Relation zu $W_3$ relevanter sind:
- $${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{245 \cdot 0.656 \cdot 10^{-3}}{32767} \hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$