Aufgaben:Aufgabe 2.08Z: „Plus” und „Mal” in GF(2 hoch 3): Unterschied zwischen den Versionen
| Zeile 58: | Zeile 58: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
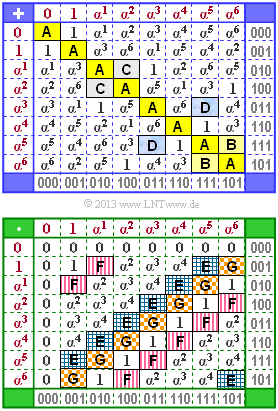
| − | '''(1)''' | + | '''(1)''' Die Addition eines jeden Elements eines Erweiterungskörpers, der auf $\rm GF(2)$ basiert, mit sich selbst ergibt stets $0$, wie man anhand der Koeffizientendarstellung leicht erkennt, zum Beispiel: |
| + | :$$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | Das heißt: „$\rm A$” steht für das Nullelement ⇒ <u>Lösungsvorschlag 1</u>. | ||
| − | |||
| + | '''(2)''' $\rm B$ ist das Ergebnis der Addition von $\alpha^5$ und $\alpha^6$ ⇒ <u>Lösungsvorschlag 3</u>: | ||
| + | :$$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$ | ||
| − | + | Man hätte dieses Ergebnis auch einfacher finden können, da in jeder Zeile und Spalte jedes Element genau einmal vorkommt. Nachdem $\rm A = 0$ festliegt, fehlt in der letzten Zeile und der letzten Spalte genau nur noch das Element $\alpha^1$. | |
| − | '''( | + | '''(3)''' $\rm C$ ist das Ergebnis der Summe von $\alpha^1$ und $\alpha^2$ ⇒ <u>Lösungsvorschlag 3</u>: |
| + | :$$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$ | ||
| − | '''( | + | '''(4)''' $\rm D$ ist das Ergebnis von $\alpha^3$ und $\alpha^5$ ⇒ <u>Lösungsvorschlag 1</u>: |
| + | :$$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 | ||
| + | \hspace{0.05cm}.$$ | ||
| − | '''(6)''' | + | '''(5)''' <u>Alle Lösungsvorschläge sind richtig, wie man aus der Zeile 2 (Multiplikation mit dem Einselelement) erkennt. Aufgrund der Gültigkeit von |
| + | :$$\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $$ | ||
| + | |||
| + | ergibt sich bei der Multiplikation eine gewisse Symmetrie, die man ebenfalls zur Lösung nutzen könnte. | ||
| + | |||
| + | Nachfolgend sehen Sie die vollständigen Tabellen für die Addition und die Multiplikation. | ||
| + | |||
| + | [[Datei:P_ID2573__KC_Z_2_8e.png|center|frame|$\rm GF(2^3)$: Vollständige Additions– und Multiplikationstabellen]] | ||
| + | |||
| + | |||
| + | '''(6)''' Richtig ist hier der <u>Lösungsvorschlag 3</u>. Alle Polynome sind zwar irreduzibel. Man benötigt aber für $\rm GF(2^3)$ ein Grad–3–Polynom. Der dritte Lösungsvorschlag ergibt sich aus der Beziehung | ||
| + | :$$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 16. Dezember 2017, 13:25 Uhr
Die Grafik zeigt die Additions– und Multiplikationstabelle für den endlichen Körper $\rm GF(2^3)$. Die Tabellen sind nicht vollständig. Einige Felder sollen Sie ergänzen.
Die Elemente sind sowohl in der Exponentendarstellung (mit roter Beschriftung, links und oben) als auch in der Koeffizientendarstellung (graue Schrift, rechts und unten) angegeben. Aus dieser Zuordnung erkennt man bereits das zugrunde liegende irreduzible Polynom $p(\alpha)$.
Additionen (und Subtraktionen) führt man am besten in der Koeffizientendarstellung (oder mit den damit fest verknüpften Polynomen) durch. Für Multiplikationen ist dagegen die Exponentendarstellung günstiger.
Hinweis:
- Die Aufgabe bezieht sich auf die Thematik der Kapitel Erweiterungskörper und Definition und Eigenschaften von Reed–Solomon–Codes.
Fragebogen
Musterlösung
- $$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 \hspace{0.05cm}.$$
Das heißt: „$\rm A$” steht für das Nullelement ⇒ Lösungsvorschlag 1.
(2) $\rm B$ ist das Ergebnis der Addition von $\alpha^5$ und $\alpha^6$ ⇒ Lösungsvorschlag 3:
- $$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$
Man hätte dieses Ergebnis auch einfacher finden können, da in jeder Zeile und Spalte jedes Element genau einmal vorkommt. Nachdem $\rm A = 0$ festliegt, fehlt in der letzten Zeile und der letzten Spalte genau nur noch das Element $\alpha^1$.
(3) $\rm C$ ist das Ergebnis der Summe von $\alpha^1$ und $\alpha^2$ ⇒ Lösungsvorschlag 3:
- $$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$
(4) $\rm D$ ist das Ergebnis von $\alpha^3$ und $\alpha^5$ ⇒ Lösungsvorschlag 1:
- $$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 \hspace{0.05cm}.$$
(5) Alle Lösungsvorschläge sind richtig, wie man aus der Zeile 2 (Multiplikation mit dem Einselelement) erkennt. Aufgrund der Gültigkeit von
- $$\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $$
ergibt sich bei der Multiplikation eine gewisse Symmetrie, die man ebenfalls zur Lösung nutzen könnte.
Nachfolgend sehen Sie die vollständigen Tabellen für die Addition und die Multiplikation.
(6) Richtig ist hier der Lösungsvorschlag 3. Alle Polynome sind zwar irreduzibel. Man benötigt aber für $\rm GF(2^3)$ ein Grad–3–Polynom. Der dritte Lösungsvorschlag ergibt sich aus der Beziehung
- $$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$