Aufgaben:Aufgabe 1.7: WDF des Rice–Fadings: Unterschied zwischen den Versionen
| Zeile 42: | Zeile 42: | ||
{Es sei $|z_0| = 2$ ⇒ $|z_0|^2 = 4$ ('''blaue Kurve'''). Wie groß ist ${\rm Pr}(a ≤ 1)$? Verwenden Sie die '''Dreiecksnäherung'''. | {Es sei $|z_0| = 2$ ⇒ $|z_0|^2 = 4$ ('''blaue Kurve'''). Wie groß ist ${\rm Pr}(a ≤ 1)$? Verwenden Sie die '''Dreiecksnäherung'''. | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(a ≤ 1)\ = \ ${ 9. | + | ${\rm Pr}(a ≤ 1)\ = \ ${ 9.4 3% } $\ \%$ |
{Es sei $|z_0|^2 = 2$ ('''rote Kurve'''). Wie groß ist ${\rm Pr}(a ≤ 1)$? Verwenden Sie die '''Dreiecksnäherung'''. | {Es sei $|z_0|^2 = 2$ ('''rote Kurve'''). Wie groß ist ${\rm Pr}(a ≤ 1)$? Verwenden Sie die '''Dreiecksnäherung'''. | ||
| Zeile 70: | Zeile 70: | ||
| − | '''(2)''' Mit dem Ergebnis der Teilaufgabe (1) erhält man: | + | '''(2)''' Mit dem Ergebnis der Teilaufgabe (1) ⇒ $f_a(a = 1) = 0.187$erhält man mit der Dreiecksnäherung: |
| − | :$${\rm Pr}(a \le 1) = | + | :$${\rm Pr}(a \le 1) = {1}/{2} \cdot 0.187 \cdot 1\hspace{0.15cm} \underline{ \approx 9.4\,\%} \hspace{0.05cm}.$$ |
Dieses Ergebnis wird etwas zu groß sein, da die blaue Kurve unterhalb der Verbindungslinie von $(0, 0)$ nach $(1, 0.187)$ liegt ⇒ konvexer Kurvenverlauf. | Dieses Ergebnis wird etwas zu groß sein, da die blaue Kurve unterhalb der Verbindungslinie von $(0, 0)$ nach $(1, 0.187)$ liegt ⇒ konvexer Kurvenverlauf. | ||
| − | '''(3)''' | + | '''(3)''' Für die rote Kurve kann der WDF–Wert $f_a(a = 1) \approx 0.35$ aus der [[Aufgaben:1.7_WDF_des_Rice%E2%80%93Fadings|Grafik]] auf der Angabenseite abgelesen werden. Daraus folgt: |
:$${\rm Pr}(a \le 1) = \frac{1}{2} \cdot 0.35 \hspace{0.15cm} \underline{ \approx 17.5\,\%} \hspace{0.05cm}.$$ | :$${\rm Pr}(a \le 1) = \frac{1}{2} \cdot 0.35 \hspace{0.15cm} \underline{ \approx 17.5\,\%} \hspace{0.05cm}.$$ | ||
| Zeile 85: | Zeile 85: | ||
:$${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -2.16) = {\rm Q}(2.16) \hspace{0.15cm} \underline{ \approx 1.5\,\%} \hspace{0.05cm}.$$ | :$${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -2.16) = {\rm Q}(2.16) \hspace{0.15cm} \underline{ \approx 1.5\,\%} \hspace{0.05cm}.$$ | ||
| − | Hierbei bezeichnet $g$ eine gaußverteilte Zufallsgröße mit dem Mittelwert $0$ und der Streuung $\sigma = 1$. Der Zahlenwert wurde mit dem | + | Hierbei bezeichnet $g$ eine gaußverteilte Zufallsgröße mit dem Mittelwert $0$ und der Streuung $\sigma = 1$. Der Zahlenwert wurde mit dem angegebenen interaktiven [[Applets:QFunction|Applet]] ermittelt. |
| − | < | + | <i>Anmerkung:</i> Die Gaußnäherung ist hier sicher mit einem gewissen Fehler verbunden: |
| + | *Aus der Grafik erkennt man, dass der Mittelwert der grünen Kurve nicht bei $a = 3.16$ liegt, sondern eher bei $3.31$. | ||
| + | *Dann ist die Leistung der Gaußnäherung $(3.31^2 + 1^2 = 12)$ genau so groß wie die der Riceverteilung: | ||
:$$|z_0|^2 + 2 \sigma^2= 10 + 2 =12\hspace{0.05cm}.$$ | :$$|z_0|^2 + 2 \sigma^2= 10 + 2 =12\hspace{0.05cm}.$$ | ||
| − | + | '''(5)''' Nach gleichem Rechenweg ersetzt man hier die Rice–WDF durch eine Gauß–WDF mit Mittelwert $\sqrt{20} \approx 4.47$ und Streuung $\sigma = 1$ und man erhält | |
| − | '''(5)''' Nach gleichem Rechenweg ersetzt man hier die Rice–WDF durch eine Gauß–WDF mit Mittelwert $20 | ||
:$${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -3.37) = {\rm Q}(3.37) { \approx 0.04\,\%} \hspace{0.05cm}.$$ | :$${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -3.37) = {\rm Q}(3.37) { \approx 0.04\,\%} \hspace{0.05cm}.$$ | ||
| − | Geht man von der leistungsgleichen Gaußverteilung aus (siehe Anmerkung zur letzten | + | Geht man von der leistungsgleichen Gaußverteilung aus (siehe Anmerkung zur letzten Teilaufgabe), so ergibt sich der Mittelwert zu $m_g = \sqrt{21}\approx 4.58$, und die Wahrscheinlichkeit wäre dann |
:$${\rm Pr}(a \le 1) \approx {\rm Q}(3.58) \hspace{0.15cm} \underline{ \approx 0.02\,\%} \hspace{0.05cm}.$$ | :$${\rm Pr}(a \le 1) \approx {\rm Q}(3.58) \hspace{0.15cm} \underline{ \approx 0.02\,\%} \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 4. Dezember 2017, 16:09 Uhr
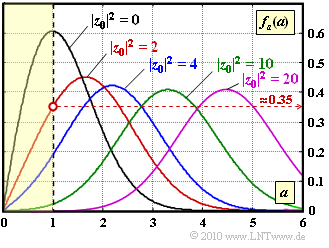
Wie aus der Grafik zu ersehen, betrachten wir das gleiche Szenario wie in Aufgabe 1.6:
- Rice–Fading mit der Varianz $\sigma^2 = 1$ der Gaußprozesse und dem Parameter $|z_0|$ für den Direktpfad.
- Hinsichtlich Direktpfad interessieren wir uns für die Parameterwerte $|z_0|^2 = 0, 2, 4, 10$ und $20$ (siehe Grafik).
- Die WDF des Betrags $a(t) = |z(t)|$ ist
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}.$$
- Die modifizierte Besselfunktion nullter Ordnung liefert folgende Werte:
- $${\rm I }_0 (2) = 2.28\hspace{0.05cm},\hspace{0.2cm}{\rm I }_0 (4) = 11.30\hspace{0.05cm},\hspace{0.2cm}{\rm I }_0 (3) = 67.23 \hspace{0.05cm}.$$
- Der quadratische Erwartungswert ⇒ Leistung des multiplikativen Faktors $|z(t)|$, ist gleich
- $${\rm E}\left [ a^2 \right ] = {\rm E}\left [ |z(t)|^2 \right ] = 2 \cdot \sigma^2 + |z_0|^2 \hspace{0.05cm}.$$
- Mit $z_0 = 0$ wird aus dem Rice–Fading das kritischere Rayleigh–Fading. In diesem Fall gilt für die Wahrscheinlichkeit, dass $a$ im gelb hintergelegten Bereich zwischen $0$ und $1$ liegt:
- $$ {\rm Pr}(a \le 1) = 1 - {\rm e}^{-0.5/\sigma^2} \approx 0.4 \hspace{0.05cm}.$$
In dieser Aufgabe soll die Wahrscheinlichkeit ${\rm Pr}(a ≤ 1)$ für $|z_0| ≠ 0$ angenähert werden. Dazu gibt es zwei Möglichkeiten, nämlich:
- die Dreiecksnäherung:
- $${\rm Pr}(a \le 1) = {1}/{2} \cdot f_a(a=1) \hspace{0.05cm}.$$
- die Gaußnäherung: Ist $|z_0| >> \sigma$, so kann die Riceverteilung durch eine Gaußverteilung mit Mittelwert $|z_0|$ und Streuung $\sigma$ angenähert werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Nichtfrequenzselektives Fading mit Direktkomponente.
- Für die numerischen Lösungen zu den letzten Teilaufgaben empfehlen wir das Interaktionsmodul: Komplementäre Gaußsche Fehlerfunktionen
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$f_a(a) = a \cdot {\rm exp} [ -\frac{a^2 + 4}{2}] \cdot {\rm I}_0 (2a)\hspace{0.05cm}.$$
Daraus ergeben sich die gesuchten Werte:
- $$f_a(a = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \cdot {\rm e}^{-2.5} \cdot {\rm I}_0 (2) = 0.082 \cdot 2.28 \hspace{0.15cm} \underline{ = 0.187}\hspace{0.05cm},$$
- $$f_a(a = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm e}^{-4} \cdot {\rm I}_0 (4) = 2 \cdot 0.0183 \cdot 11.3 \hspace{0.15cm} \underline{ = 0.414}\hspace{0.05cm},$$
- $$f_a(a = 3) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \cdot {\rm e}^{-6.5} \cdot {\rm I}_0 (6) = 3 \cdot 0.0015 \cdot 67.23 \hspace{0.15cm} \underline{ = 0.303}\hspace{0.05cm}.$$
Die Ergebnisse passen gut zu der blauen Kurve auf der Angabenseite.
(2) Mit dem Ergebnis der Teilaufgabe (1) ⇒ $f_a(a = 1) = 0.187$erhält man mit der Dreiecksnäherung:
- $${\rm Pr}(a \le 1) = {1}/{2} \cdot 0.187 \cdot 1\hspace{0.15cm} \underline{ \approx 9.4\,\%} \hspace{0.05cm}.$$
Dieses Ergebnis wird etwas zu groß sein, da die blaue Kurve unterhalb der Verbindungslinie von $(0, 0)$ nach $(1, 0.187)$ liegt ⇒ konvexer Kurvenverlauf.
(3) Für die rote Kurve kann der WDF–Wert $f_a(a = 1) \approx 0.35$ aus der Grafik auf der Angabenseite abgelesen werden. Daraus folgt:
- $${\rm Pr}(a \le 1) = \frac{1}{2} \cdot 0.35 \hspace{0.15cm} \underline{ \approx 17.5\,\%} \hspace{0.05cm}.$$
Dieser Wahrscheinlichkeitswert wird etwas zu klein sein, da die rote Kurve im Bereich zwischen $0$ und $1$ konkav verläuft.
(4) Die Gaußnäherung besagt, dass man die Riceverteilung durch eine Gaußverteilung mit Mittelwert $|z_0| = 3.16$ und Streuung $\sigma = 1$ annähern kann, wenn der Quotient $|z_0|/\sigma$ hinreichend groß ist. Dann gilt:
- $${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -2.16) = {\rm Q}(2.16) \hspace{0.15cm} \underline{ \approx 1.5\,\%} \hspace{0.05cm}.$$
Hierbei bezeichnet $g$ eine gaußverteilte Zufallsgröße mit dem Mittelwert $0$ und der Streuung $\sigma = 1$. Der Zahlenwert wurde mit dem angegebenen interaktiven Applet ermittelt.
Anmerkung: Die Gaußnäherung ist hier sicher mit einem gewissen Fehler verbunden:
- Aus der Grafik erkennt man, dass der Mittelwert der grünen Kurve nicht bei $a = 3.16$ liegt, sondern eher bei $3.31$.
- Dann ist die Leistung der Gaußnäherung $(3.31^2 + 1^2 = 12)$ genau so groß wie die der Riceverteilung:
- $$|z_0|^2 + 2 \sigma^2= 10 + 2 =12\hspace{0.05cm}.$$
(5) Nach gleichem Rechenweg ersetzt man hier die Rice–WDF durch eine Gauß–WDF mit Mittelwert $\sqrt{20} \approx 4.47$ und Streuung $\sigma = 1$ und man erhält
- $${\rm Pr}(a \le 1) \approx {\rm Pr}(g \le -3.37) = {\rm Q}(3.37) { \approx 0.04\,\%} \hspace{0.05cm}.$$
Geht man von der leistungsgleichen Gaußverteilung aus (siehe Anmerkung zur letzten Teilaufgabe), so ergibt sich der Mittelwert zu $m_g = \sqrt{21}\approx 4.58$, und die Wahrscheinlichkeit wäre dann
- $${\rm Pr}(a \le 1) \approx {\rm Q}(3.58) \hspace{0.15cm} \underline{ \approx 0.02\,\%} \hspace{0.05cm}.$$