Aufgaben:Aufgabe 1.6: Zum (7, 4)–Hamming–Code: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
|||
| (12 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2388__KC_A_1_6_neu.png|right|frame| | + | [[Datei:P_ID2388__KC_A_1_6_neu.png|right|frame|Codetabelle des $\text{HC (7, 4)}$]] |
| − | 1962 hat [ | + | 1962 hat [https://de.wikipedia.org/wiki/Richard_Hamming Richard Wesley Hamming] eine Klasse binärer Blockcodes angegeben, die sich durch die Anzahl $m$ der zugeführten Prüfbits unterscheiden. Die Codewortlänge ist stets $n = 2^m - 1$. Das Informationswort besteht aus $k = n - m$ Bit: |
| + | |||
| + | *$m = 2$: $\text{(3, 1)}$–Hamming–Code ⇒ identisch mit [[Kanalcodierung/Beispiele_binärer_Blockcodes#Wiederholungscodes|$\text{RC (3, 1)}$]], | ||
| + | *$m = 3$: $\text{(7, 4)}$–Hamming–Code, | ||
| + | *$m = 4$: $\text{(15, 11)}$–Hamming–Code, | ||
| + | *$m = 5$: $\text{(31, 26)}$–Hamming–Code, usw. | ||
| − | |||
| − | |||
| − | |||
| − | |||
Im Verlaufe dieser Aufgabe gibt es Fragen | Im Verlaufe dieser Aufgabe gibt es Fragen | ||
| − | *zum Codeumfang | | + | *zum Codeumfang $ |\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}|$, |
| − | *zur Coderate | + | *zur Coderate $R$, und |
| − | *zur minimalen Distanz $d_{\rm min}$ | + | *zur minimalen Distanz $d_{\rm min}$. |
| + | |||
| + | |||
| + | Weiterhin soll geklärt werden, ob der für diese Aufgabe durch seine Codetabelle $\underline{u}_{i} ⇒ \underline{x}_{i}$ gegebene $\text{(7, 4)}$–Hamming–Code systematisch ist, und ob es sich um einen so genannten „perfekten Code” handelt. Der Laufindex kann die Werte $i = 1, \text{...}\hspace{0.05cm} , 2^k =16$ annehmen. | ||
| + | |||
| + | Man spricht von einem ''perfekten Code'', wenn folgende Bedingung erfüllt ist: | ||
| + | :$$2^k = \frac{2^n} {\sum_{f=0}^t {n \choose f}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | Hierbei bezeichnet $t$ die Anzahl der korrigierbaren Fehler. Bei ungerader Minimaldistanz $d_{\rm min}$ gilt: | ||
| + | :$$ t = \frac{d_{\rm min}-1 } {2} \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Interpretation zu dieser Bedingung finden Sie in der Musterlösung. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Hinweise:'' | |
| − | : | + | *Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Beispiele_binärer_Blockcodes|Beispiele binärer Blockcodes]]. |
| + | *Bezug genommen wird insbesondere auf die Seite [[Kanalcodierung/Beispiele_binärer_Blockcodes#Hamming.E2.80.93Codes|Hamming–Codes]]. | ||
| + | |||
| + | *Für diesen Hamming–Code wurden andere Prüfgleichungen herangezogen als im [[Kanalcodierung/Beispiele_binärer_Blockcodes#Hamming.E2.80.93Codes|Theorieteil]]. Deshalb unterscheiden sich auch die Codetabellen. | ||
| + | *In der [[Aufgaben:Aufgabe_1.07:_Prüf-_und_Generatormatrix_des_HC_(7,_4,_3)|Aufgabe 1.7]], bei der der gleiche Code verwendet wird, ist das Schaubild der Prüfgleichungen angegeben. | ||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Zeile 42: | Zeile 48: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie die Kenngrößen des gegebenen Codes | + | {Geben Sie die Kenngrößen des gegebenen Codes $\mathcal{C}$ an: |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $ |\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| \ = \ $ { 16 } |
| − | $\ | + | $ k \hspace{0.46cm} = \ $ { 4 } |
| − | $\ | + | $ n \hspace{0.44cm} = \ $ { 7 } |
| − | $\ | + | $ R \hspace{0.40cm} = \ $ { 0.571 3% } |
{Handelt es sich um einen systematischen Code? | {Handelt es sich um einen systematischen Code? | ||
| − | |type=" | + | |type="()"} |
+ Ja, | + Ja, | ||
- Nein. | - Nein. | ||
| Zeile 57: | Zeile 63: | ||
{Wie groß ist die minimale Distanz zwischen zwei beliebigen Codeworten? | {Wie groß ist die minimale Distanz zwischen zwei beliebigen Codeworten? | ||
|type="{}"} | |type="{}"} | ||
| − | $ \ d_{\rm min}$ | + | $ \ d_{\rm min} \ = \ $ { 3 } |
| − | {Wieviele Übertragungsfehler können erkannt ( | + | {Wieviele Übertragungsfehler können erkannt $(e)$ bzw. korrigiert $(t)$ werden? |
|type="{}"} | |type="{}"} | ||
| − | $ \ | + | $e\hspace{0.22cm} = \ $ { 2 } |
| − | $ \ | + | $t\hspace{0.28cm} = \ $ { 1 } |
| − | |||
| − | |||
| − | |||
{Ist der hier betrachtete Hamming–Code perfekt? | {Ist der hier betrachtete Hamming–Code perfekt? | ||
| − | |type=" | + | |type="()"} |
+ Ja, | + Ja, | ||
- Nein. | - Nein. | ||
| Zeile 74: | Zeile 77: | ||
{Welche Aussagen gelten hinsichtlich eines perfekten Codes? | {Welche Aussagen gelten hinsichtlich eines perfekten Codes? | ||
|type="[]"} | |type="[]"} | ||
| − | - Ein perfekter Code führt stets | + | - Ein perfekter Code führt stets zur Blockfehlerwahrscheinlichkeit Null. |
| − | + Alle Empfangsworte | + | + Alle Empfangsworte $\underline{y}$ sind einem gültigen Codewort zuordbar. |
+ Bei perfekten Codes ist die minimale Hamming–Distanz ungerade. | + Bei perfekten Codes ist die minimale Hamming–Distanz ungerade. | ||
| − | {Welche der nachfolgend | + | {Welche der nachfolgend aufgeführten Codes sind perfekt? |
|type="[]"} | |type="[]"} | ||
| − | + (15,11)–Hamming–Code, | + | + Der $\text{(15, 11)}$–Hamming–Code, |
| − | + (63,57)–Hamming–Code, | + | + der $\text{(63, 57)}$–Hamming–Code, |
| − | + (3,1)–Repetition Code, | + | + der $\text{(3, 1)}$–Repetition Code, |
| − | - (4,1)–Repetition Code, | + | - der $\text{(4, 1)}$–Repetition Code, |
| − | + (5,1)–Repetition Code. | + | + der $\text{(5, 1)}$–Repetition Code. |
| Zeile 91: | Zeile 94: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Die Codetabelle hat 16 Einträge: $\underline{|C| = 16}$. |
| − | '''2.''' | + | *Aus der Gleichung $|C| = 2^k$ folgt damit $\underline{k = 4}$. |
| − | '''3.''' | + | *Die Länge eines jeden Codewortes ist $\underline{n = 7}$. |
| − | '''4 | + | *Damit ist die Coderate $\underline{R = 4/7} = 0.571$. |
| − | '''5 | + | |
| − | '''6.''' | + | |
| − | '''7.''' | + | |
| + | '''(2)''' Richtig ist <u>JA</u>: | ||
| + | *Jedes Codewort $\underline{x}$ beinhaltet zunächst die $k = 4$ Bit des Informationswortes $\underline{u}$. Danach folgen $m = 3$ Prüfbits: | ||
| + | :$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_5,x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3) \hspace{0.05cm}.$$ | ||
| + | *Dies entspricht genau der Definition eines [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes|systematischen Codes]] . | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Bei jedem Hamming–Code beträgt die minimale Distanz $d_{\rm min} \underline{= 3}$. | ||
| + | *Aus der Tabelle erkennt man dies daran, dass das minimale [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung|Hamming–Gewicht]] (die Anzahl der Einsen in einem Codewort) gleich 3 ist. | ||
| + | *Ein linearer Code beinhaltet nämlich auch das Nullwort, so dass gilt: | ||
| + | :$$d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} }\hspace{0.1cm}w_{\rm H}(\underline{x}) = 3 \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' Die Angabe $d_{\rm min} = 3$ bedeutet, dass $\underline{e = 2}$ Fehler erkannt und $\underline{t = 1}$ Fehler korrigiert werden können. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Richtig ist <u>JA</u>: | ||
| + | *Die Bedingung für einen perfekten Code lautet entsprechend der Angabe: | ||
| + | |||
| + | :$$ 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Beim hier betrachteten (7, 4)–Hamming–Code gilt $n = 7$, $m = 3$ und $t = 1$, so dass sich auf beiden Seiten der Gleichung der Wert 8 ergibt: | ||
| + | |||
| + | :$$ 2^3 = 8\hspace{0.05cm}, \hspace{0.35cm} {\sum_{f=0}^1 {7 \choose f}} = {7 \choose 0} + {7 \choose 1} = 1 + 7 = 8 \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Richtig sind die <u>Aussagen 2 und 3 </u>: | ||
| + | *Gäbe es einen Kanalcode mit endlicher Codewortlänge $n$, der für alle Kanäle die Blockfehlerwahrscheinlichkeit zu Null macht, so wäre dieser nicht nur perfekt, sondern ein Wunder. | ||
| + | *Aufgrund des Kanalcodierungstheorems ist aber ${\rm Pr(Blockfehler)} = 0$ bei endlichem $n$ gar nicht möglich. | ||
| + | |||
| + | |||
| + | [[Datei:P_ID2389__KC_A_1_6_ML.png|right|frame|Verdeutlichung eines perfekten Codes]] | ||
| + | |||
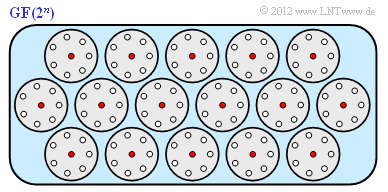
| + | Veranschaulichen wir uns die Aussage 2 durch eine Grafik. Der hochdimensionale Raum ist hierbei stark vereinfacht (in 2D) dargestellt. Wir gehen dabei von den Zahlenwerten $k = 4$, $n = 7$, $m = 3$ und $t = 1$ des (7, 4, 3)–Hamming–Codes aus: | ||
| + | |||
| + | *Für das Empfangswort sind $2^7 = 128$ Punkte im 7–dimensionalen Raum möglich. Die roten Punkte markieren die $2^4 = 16$ gültigen Codeworte. | ||
| + | |||
| + | *Die Kreise umfassen jeweils 8 Punkte, nämlich ein gültiges Codewort und $n = 7$ Empfangsworte nach nur einem Fehler, die man bei der Decodierung genau diesem Codewort zuordnet. | ||
| + | |||
| + | *Insgesamt gibt es $2^4 = 16$ solcher Kreise. Wegen $128 = 16 · 8$ liegt deshalb kein einziges Empfangswort $\underline{y}$ außerhalb eines solchen Zuordnungskreises. | ||
| + | |||
| + | |||
| + | Auch die <u>letzte Aussage</u> ist zutreffend, was beispielhaft für $d_{\rm min} = 4$ gezeigt werden soll: | ||
| + | *Hiermit kann ebenfalls nur $t = 1$ Fehler korrigiert werden. | ||
| + | *Unterscheidet sich ein Empfangswort $\underline{y}$ von zulässigen Codeworten in zwei Bit, so ist dieser Punkt keinem Kreis zuzuordnen. Es liegen dann auch Punkte außerhalb der Kreise und die Bedingung eines perfekten Codes ist nicht mehr erfüllt. | ||
| + | |||
| + | |||
| + | |||
| + | '''(7)''' Richtig sind die <u>Aussagen 1, 2, 3 und 5</u>: | ||
| + | *Alle Hamming–Codes haben die minimale Hamming–Distanz $d_{\rm min} = 3$ ⇒ $t = 1$. | ||
| + | *Gleichzeitig lässt sich jeder $(n, k)$–Hamming–Code auch als $(2^m – 1, 2^m – 1 – m)$ Code schreiben, wobei $m = n – k$ die Anzahl der Prüfbits angibt. | ||
| + | *Damit wird die Gleichung eines perfekten Codes stets erfüllt: | ||
| + | |||
| + | :$${\sum_{f=0}^1 {n \choose f}} = 1 + n = 2^m \hspace{0.05cm}.$$ | ||
| + | |||
| + | Hierbei bedeuten: | ||
| + | *$m = 2$: (3, 1) Hamming–Code, ⇒ identisch mit [[Kanalcodierung/Beispiele_binärer_Blockcodes#Wiederholungscodes|'''RC (3, 1)''',]] | ||
| + | *$m = 3$: (7, 4) Hamming–Code, | ||
| + | *$m = 4$: (15, 11) Hamming–Code, | ||
| + | *$m = 5$: (31, 26) Hamming–Code, | ||
| + | *$m = 6$: (63, 57) Hamming–Code, | ||
| + | |||
| + | |||
| + | Auch der Wiederholungscode mit $n = 5$ erfüllt die Bedingung. Mit $d_{\rm min} = 5$, $t = 2$ und $m = 4$ erhält man: | ||
| + | :$${\sum_{f=0}^2 {5 \choose f}} = 1 + 5 + 10 = 16 = 2^m \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die anderen Wiederholungscodes (RC) mit ungeradem $n$ sind ebenfalls perfekt, nicht jedoch mit geradem $n$: RC (4, 1), RC (6, 1), usw. Dies wurde bereits in der Musterlösung zur Teilaufgabe '''(6)''' begründet. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 7. Mai 2019, 18:58 Uhr
1962 hat Richard Wesley Hamming eine Klasse binärer Blockcodes angegeben, die sich durch die Anzahl $m$ der zugeführten Prüfbits unterscheiden. Die Codewortlänge ist stets $n = 2^m - 1$. Das Informationswort besteht aus $k = n - m$ Bit:
- $m = 2$: $\text{(3, 1)}$–Hamming–Code ⇒ identisch mit $\text{RC (3, 1)}$,
- $m = 3$: $\text{(7, 4)}$–Hamming–Code,
- $m = 4$: $\text{(15, 11)}$–Hamming–Code,
- $m = 5$: $\text{(31, 26)}$–Hamming–Code, usw.
Im Verlaufe dieser Aufgabe gibt es Fragen
- zum Codeumfang $ |\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}|$,
- zur Coderate $R$, und
- zur minimalen Distanz $d_{\rm min}$.
Weiterhin soll geklärt werden, ob der für diese Aufgabe durch seine Codetabelle $\underline{u}_{i} ⇒ \underline{x}_{i}$ gegebene $\text{(7, 4)}$–Hamming–Code systematisch ist, und ob es sich um einen so genannten „perfekten Code” handelt. Der Laufindex kann die Werte $i = 1, \text{...}\hspace{0.05cm} , 2^k =16$ annehmen.
Man spricht von einem perfekten Code, wenn folgende Bedingung erfüllt ist:
- $$2^k = \frac{2^n} {\sum_{f=0}^t {n \choose f}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$
Hierbei bezeichnet $t$ die Anzahl der korrigierbaren Fehler. Bei ungerader Minimaldistanz $d_{\rm min}$ gilt:
- $$ t = \frac{d_{\rm min}-1 } {2} \hspace{0.05cm}.$$
Die Interpretation zu dieser Bedingung finden Sie in der Musterlösung.
Hinweise:
- Die Aufgabe gehört zum Kapitel Beispiele binärer Blockcodes.
- Bezug genommen wird insbesondere auf die Seite Hamming–Codes.
- Für diesen Hamming–Code wurden andere Prüfgleichungen herangezogen als im Theorieteil. Deshalb unterscheiden sich auch die Codetabellen.
- In der Aufgabe 1.7, bei der der gleiche Code verwendet wird, ist das Schaubild der Prüfgleichungen angegeben.
Fragebogen
Musterlösung
- Aus der Gleichung $|C| = 2^k$ folgt damit $\underline{k = 4}$.
- Die Länge eines jeden Codewortes ist $\underline{n = 7}$.
- Damit ist die Coderate $\underline{R = 4/7} = 0.571$.
(2) Richtig ist JA:
- Jedes Codewort $\underline{x}$ beinhaltet zunächst die $k = 4$ Bit des Informationswortes $\underline{u}$. Danach folgen $m = 3$ Prüfbits:
- $$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_5,x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3) \hspace{0.05cm}.$$
- Dies entspricht genau der Definition eines systematischen Codes .
(3) Bei jedem Hamming–Code beträgt die minimale Distanz $d_{\rm min} \underline{= 3}$.
- Aus der Tabelle erkennt man dies daran, dass das minimale Hamming–Gewicht (die Anzahl der Einsen in einem Codewort) gleich 3 ist.
- Ein linearer Code beinhaltet nämlich auch das Nullwort, so dass gilt:
- $$d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} }\hspace{0.1cm}w_{\rm H}(\underline{x}) = 3 \hspace{0.05cm}.$$
(4) Die Angabe $d_{\rm min} = 3$ bedeutet, dass $\underline{e = 2}$ Fehler erkannt und $\underline{t = 1}$ Fehler korrigiert werden können.
(5) Richtig ist JA:
- Die Bedingung für einen perfekten Code lautet entsprechend der Angabe:
- $$ 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$
- Beim hier betrachteten (7, 4)–Hamming–Code gilt $n = 7$, $m = 3$ und $t = 1$, so dass sich auf beiden Seiten der Gleichung der Wert 8 ergibt:
- $$ 2^3 = 8\hspace{0.05cm}, \hspace{0.35cm} {\sum_{f=0}^1 {7 \choose f}} = {7 \choose 0} + {7 \choose 1} = 1 + 7 = 8 \hspace{0.05cm}.$$
(6) Richtig sind die Aussagen 2 und 3 :
- Gäbe es einen Kanalcode mit endlicher Codewortlänge $n$, der für alle Kanäle die Blockfehlerwahrscheinlichkeit zu Null macht, so wäre dieser nicht nur perfekt, sondern ein Wunder.
- Aufgrund des Kanalcodierungstheorems ist aber ${\rm Pr(Blockfehler)} = 0$ bei endlichem $n$ gar nicht möglich.
Veranschaulichen wir uns die Aussage 2 durch eine Grafik. Der hochdimensionale Raum ist hierbei stark vereinfacht (in 2D) dargestellt. Wir gehen dabei von den Zahlenwerten $k = 4$, $n = 7$, $m = 3$ und $t = 1$ des (7, 4, 3)–Hamming–Codes aus:
- Für das Empfangswort sind $2^7 = 128$ Punkte im 7–dimensionalen Raum möglich. Die roten Punkte markieren die $2^4 = 16$ gültigen Codeworte.
- Die Kreise umfassen jeweils 8 Punkte, nämlich ein gültiges Codewort und $n = 7$ Empfangsworte nach nur einem Fehler, die man bei der Decodierung genau diesem Codewort zuordnet.
- Insgesamt gibt es $2^4 = 16$ solcher Kreise. Wegen $128 = 16 · 8$ liegt deshalb kein einziges Empfangswort $\underline{y}$ außerhalb eines solchen Zuordnungskreises.
Auch die letzte Aussage ist zutreffend, was beispielhaft für $d_{\rm min} = 4$ gezeigt werden soll:
- Hiermit kann ebenfalls nur $t = 1$ Fehler korrigiert werden.
- Unterscheidet sich ein Empfangswort $\underline{y}$ von zulässigen Codeworten in zwei Bit, so ist dieser Punkt keinem Kreis zuzuordnen. Es liegen dann auch Punkte außerhalb der Kreise und die Bedingung eines perfekten Codes ist nicht mehr erfüllt.
(7) Richtig sind die Aussagen 1, 2, 3 und 5:
- Alle Hamming–Codes haben die minimale Hamming–Distanz $d_{\rm min} = 3$ ⇒ $t = 1$.
- Gleichzeitig lässt sich jeder $(n, k)$–Hamming–Code auch als $(2^m – 1, 2^m – 1 – m)$ Code schreiben, wobei $m = n – k$ die Anzahl der Prüfbits angibt.
- Damit wird die Gleichung eines perfekten Codes stets erfüllt:
- $${\sum_{f=0}^1 {n \choose f}} = 1 + n = 2^m \hspace{0.05cm}.$$
Hierbei bedeuten:
- $m = 2$: (3, 1) Hamming–Code, ⇒ identisch mit RC (3, 1),
- $m = 3$: (7, 4) Hamming–Code,
- $m = 4$: (15, 11) Hamming–Code,
- $m = 5$: (31, 26) Hamming–Code,
- $m = 6$: (63, 57) Hamming–Code,
Auch der Wiederholungscode mit $n = 5$ erfüllt die Bedingung. Mit $d_{\rm min} = 5$, $t = 2$ und $m = 4$ erhält man:
- $${\sum_{f=0}^2 {5 \choose f}} = 1 + 5 + 10 = 16 = 2^m \hspace{0.05cm}.$$
Die anderen Wiederholungscodes (RC) mit ungeradem $n$ sind ebenfalls perfekt, nicht jedoch mit geradem $n$: RC (4, 1), RC (6, 1), usw. Dies wurde bereits in der Musterlösung zur Teilaufgabe (6) begründet.