Aufgaben:Aufgabe 1.6: Wurzel-Nyquist-System

• Zurück zum Buch

Cosinus-Spektrum

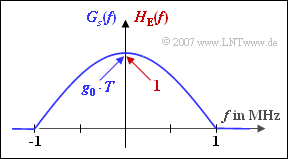
Die nebenstehende Grafik zeigt

• das Spektrum $G_{s}(f)$ des Sendegrundimpulses,
• den Frequenzgang $H_{\rm E}(f)$ des Empfangsfilters

eines binären und bipolaren Übertragungssystems, die zueinander formgleich sind:

$$G_s(f) = \left\{ \begin{array}{c} A \cdot \cos \left( \frac {\pi \cdot f}{2 \cdot f_2} \right) \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ \\ \end{array} \begin{array}{*{20}c}|f| \le f_2 \hspace{0.05cm}, \\ \\ {\rm sonst }\hspace{0.05cm}, \\ \end{array}$$

$$H_{\rm E }(f) = \left\{ \begin{array}{c} 1 \cdot \cos \left( \frac {\pi \cdot f}{2 \cdot f_2} \right) \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ \\ \end{array} \begin{array}{*{20}c}|f| \le f_2 \hspace{0.05cm}, \\ \\ {\rm sonst }\hspace{0.05cm}. \\ \end{array}$$

In der gesamten Aufgabe gelte $A = 10^{–6} \ \rm V/Hz$ und $f_{2} = 1 \ \rm MHz$.

Unter der Voraussetzung, dass die Bitrate $R = 1/T$ richtig gewählt wird, erfüllt der Detektionsgrundimpuls $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$ das erste Nyquistkriterium. Bei der dazugehörigen Spektralfunktion $G_{d}(f)$ erfolgt dabei der Flankenabfall cosinusförmig ähnlich einem Cosinus–Rolloff–Spektrum; der Rolloff–Faktor $r$ ist in dieser Aufgabe zu ermitteln.

Hinweis:

• Die Aufgabe bezieht sich auf das Optimierung der Basisbandübertragungssystemedieses Buches. Zahlenwerte der Q–Funktion liefert zum Beispiel das folgende Interaktionsmodul: Komplementäre Gaußsche Fehlerfunktionen
• Der Crestfaktor ist der Qotient aus Maximalwert und Effektivwert des Sendesignals und damit ein Maß für die sendeseitigen Impulsinterferenzen:

$$C_{\rm S} = \frac{s_0}{\sqrt{E_{\rm B}/T}} = \frac{{\rm Max}[s(t)]}{\sqrt{{\rm E}[s^2(t)]}}= {s_0}/{s_{\rm eff}}.$$

Fragebogen

1

Berechnen Sie das Nyquistspektrum $G_{d}(f)$. Wie groß sind Nyquistfrequenz und Rolloff–Faktor?

$f_{\rm Nyq} \ = \ $ $\ \rm MHz$

$r \ = \ $

2

Wie groß ist die Bitrate des vorliegenden Nyquistsystems?

$R \ = \ $ $\ \rm Mbit/s$

3

Warum handelt es sich unter der Nebenbedingung „Leistungsbegrenzung” um ein optimales System?

	Das Gesamtsystem erfüllt die Nyquistbedingung.
	Der Crestfaktor ist $C_{\rm S} = 1$.
	Das Empfangsfilter ist an den Sendegrundimpuls angepasst.

4

Welche Bitfehlerwahrscheinlichkeit ergibt sich, wenn für die Leistungsdichte des AWGN–Rauschens $N_{0} = 8 \cdot 10^{–8}\ \rm V^{2}/Hz$ (bezogen auf $1 Ω$) gilt?

$p_{\rm B} \ = \ $ $\ \cdot 10^{-6}$

Musterlösung

Musterlösung

(1)  Mit den Funktionen $G_{s}(f)$ und $H_{\rm E}(f)$ gilt für das Spektrum des Detektionsgrundimpulses für $|f| \leq f_{2}$:

$$G_d(f) = G_s(f) \cdot H_{\rm E}(f) = A \cdot \cos^2 \left( \frac {\pi \cdot f}{2 \cdot f_2} \right).$$

Nach der allgemeinen Definition des Cosinus–Rolloff–Spektrums ergeben sich die Eckfrequenzen $f_{1} = 0$ und $f_{2} = 1\ \rm MHz$. Daraus folgt für die Nyquistfrequenz (Symmetriepunkt bezüglich des Flankenabfalls):

$$f_{\rm Nyq} = \frac{f_1 +f_2 } {2 } \hspace{0.1cm}\underline { = 0.5\,{\rm MHz}}\hspace{0.05cm}.$$

Der Rolloff–Faktor beträgt

$$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.1cm}\underline {= 1} \hspace{0.05cm}.$$

Das bedeutet: $G_{d}(f)$ beschreibt ein cos$^{2}$–Spektrum.

(2)  Der Zusammenhang zwischen Nyquistfrequenz und Symboldauer $T$ lautet $f_{\rm Nyq} = 1/(2T)$. Daraus folgt für die Bitrate $R = 1/T = 2 \cdot f_{\rm Nyq}\ \underline{= 1 \ \rm Mbit/s}$. Beachten Sie die unterschiedlichen Einheiten für Frequenz und Bitrate.

(3)  Es handelt es sich um ein optimales Binärsystem unter der Nebenbedingung der Leistungsbegrenzung, weil die erste und die dritte Lösungsalternative zutreffen. Der Crestfaktor ist bei Leistungsbegrenzung nicht von Bedeutung. Bei den hier gegebenen Voraussetzungen würde $C_{\rm S} > 1$ gelten.

(4)  Die Bitfehlerwahrscheinlichkeit eines optimalen Systems kann wie folgt berechnet werden:

$$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$

Im vorliegenden Beispiel erhält man für die mittlere Energie pro Bit:

$$E_{\rm B} = \ \int_{-\infty}^{+\infty}|G_s(f)|^2 \,{\rm d} f = A^2 \cdot \int_{-1/T}^{+1/T} H_{\rm Nyq}(f) \,{\rm d} f = \ \frac {A^2}{T} = \frac {(10^{-6}\,{\rm V/Hz})^2}{10^{-6}\,{\rm s}} = 10^{-6}\,{\rm V^2s}\hspace{0.05cm}.$$

Mit $N_{0} = 8 \cdot 10^{–8} \ \rm V^{2}/Hz$ ergibt sich weiter:

$$p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot 10^{-6}\,{\rm V^2s}}{8 \cdot 10^{-8}\,{\rm V^2/Hz}}}\right)= {\rm Q} \left( \sqrt{25}\right)= {\rm Q} (5) \hspace{0.1cm}\underline {= 0.287 \cdot 10^{-6}}\hspace{0.05cm}.$$