Aufgaben:Aufgabe 1.5: Cosinus-Quadrat-Spektrum: Unterschied zwischen den Versionen
| Zeile 64: | Zeile 64: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die obere Eckfrequenz kann aus der Grafik abgelesen werden: | + | '''(1)''' Die obere Eckfrequenz kann aus der Grafik abgelesen werden: Da das Spektrum in keinem Bereich konstant ist, gilt $f_{1} \underline {= 0}$. |
| − | |||
| Zeile 71: | Zeile 70: | ||
:$$f_{\rm Nyq} = \ \frac{f_1 +f_2 } | :$$f_{\rm Nyq} = \ \frac{f_1 +f_2 } | ||
{2 }\hspace{0.1cm}\underline { = 1\,{\rm MHz}}\hspace{0.05cm},\hspace{0.5cm} r = \ \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.1cm}\underline { = 1 }\hspace{0.05cm}.$$ | {2 }\hspace{0.1cm}\underline { = 1\,{\rm MHz}}\hspace{0.05cm},\hspace{0.5cm} r = \ \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.1cm}\underline { = 1 }\hspace{0.05cm}.$$ | ||
| − | |||
'''(3)''' Der Abstand äquidistanter Nulldurchgänge hängt direkt mit der Nyquistfrequenz zusammen: | '''(3)''' Der Abstand äquidistanter Nulldurchgänge hängt direkt mit der Nyquistfrequenz zusammen: | ||
:$$f_{\rm Nyq}= \frac{1}{2T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T= \frac{1}{2f_{\rm Nyq}}\hspace{0.1cm}\underline { = 0.5\,{\rm µ s}}\hspace{0.05cm}.$$ | :$$f_{\rm Nyq}= \frac{1}{2T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T= \frac{1}{2f_{\rm Nyq}}\hspace{0.1cm}\underline { = 0.5\,{\rm µ s}}\hspace{0.05cm}.$$ | ||
| − | + | '''(4)''' Richtig sind die <u>Aussagen 1 und 3</u>: | |
| − | '''(4)''' Richtig sind die <u>Aussagen 1 und 3</u>: | + | *Die erste Aussage ist richtig: Die Funktion $si(π · t/T)$ führt zu Nulldurchgängen bei $\nu T\ (\nu \neq 0)$. |
| − | *Die erste Aussage ist richtig: Die Funktion $si(π · t/T)$ führt zu Nulldurchgängen bei $\nu T (\nu \neq 0)$. | + | *Auch die letzte Aussage trifft zu: Wegen $g(t) = 0$ für $t =\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ wird auch das zweite Nyquistkriterium erfüllt. |
| − | *Auch die letzte Aussage trifft zu: Wegen $g(t) = 0$ für $t =\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ wird auch das zweite Nyquistkriterium erfüllt. | + | *Falsch ist dagegen die mittlere Aussage, da $g(t = T/2) \neq 0$ ist. |
| − | *Falsch ist dagegen die mittlere Aussage, da $g(t = T/2) \neq 0$ ist. | ||
| − | |||
*Die Bedingung für das zweite Nyquistkriterium lautet im Frequenzbereich: | *Die Bedingung für das zweite Nyquistkriterium lautet im Frequenzbereich: | ||
:$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} \frac {G \left ( f - | :$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} \frac {G \left ( f - | ||
\frac{k}{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= | \frac{k}{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= | ||
{\rm const.}$$ | {\rm const.}$$ | ||
| − | *Die Bedingung ist beim cos$^{2}$–Spektrum tatsächlich erfüllt, wie man nach längerer Rechnung zeigen kann. Wir beschränken uns hier auf den Frequenzbereich $| f · T | \leq 1$ und setzen vereinfachend $g_{0} \cdot T = 1$: | + | *Die Bedingung ist beim cos$^{2}$–Spektrum tatsächlich erfüllt, wie man nach längerer Rechnung zeigen kann. Wir beschränken uns hier auf den Frequenzbereich $| f · T | \leq 1$ und setzen vereinfachend $g_{0} \cdot T = 1$: |
:$$G_{\rm Per}(f) = \frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} | :$$G_{\rm Per}(f) = \frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} | ||
- f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) | - f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) | ||
| Zeile 100: | Zeile 96: | ||
- f) \cdot T \right ]} +1- \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} | - f) \cdot T \right ]} +1- \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} | ||
+ f) \cdot T \right ]}\right ]\hspace{0.05cm}.$$ | + f) \cdot T \right ]}\right ]\hspace{0.05cm}.$$ | ||
| − | * Wegen $\cos \left [ \pi \cdot ( f_{\rm Nyq} \pm f) \cdot T \right] = \cos | + | * Wegen $\cos \left [ \pi \cdot ( f_{\rm Nyq} \pm f) \cdot T \right] = \cos |
\left ( {\pi}/{2} \pm \pi f T \right) = \sin \left ( \pm | \left ( {\pi}/{2} \pm \pi f T \right) = \sin \left ( \pm | ||
\pi f T \right)\text{:}$ | \pi f T \right)\text{:}$ | ||
| Zeile 107: | Zeile 103: | ||
| − | '''(5)''' Für $t = T/2$ liefert die angegebene Gleichung einen unbestimmten Wert (0 geteilt durch 0), der mit der Regel von l'Hospital ermittelt werden kann. | + | '''(5)''' Für $t = T/2$ liefert die angegebene Gleichung einen unbestimmten Wert ("0 geteilt durch 0"), der mit der Regel von l'Hospital ermittelt werden kann. |
| − | *Dazu bildet man die Ableitungen von Zähler und Nenner und setzt in das Ergebnis den gewünschten Zeitpunkt $t = T/2$ ein: | + | *Dazu bildet man die Ableitungen von Zähler und Nenner und setzt in das Ergebnis den gewünschten Zeitpunkt $t = T/2$ ein: |
:$$\frac{g( t = T/2)}{g_0} = \ {{\rm si}(\pi \cdot \frac{t}{T}) | :$$\frac{g( t = T/2)}{g_0} = \ {{\rm si}(\pi \cdot \frac{t}{T}) | ||
| Zeile 133: | Zeile 129: | ||
\cdot t/T)(1- 2 \cdot t/T)}= \frac{\cos(\pi \cdot t/T)}{1 - (2 | \cdot t/T)(1- 2 \cdot t/T)}= \frac{\cos(\pi \cdot t/T)}{1 - (2 | ||
\cdot t/T)^2}\hspace{0.05cm}.$$ | \cdot t/T)^2}\hspace{0.05cm}.$$ | ||
| − | *Daraus folgt, dass beide Ausdrücke tatsächlich gleich sind. Für den Zeitpunkt $t = T/2$ gilt somit weiterhin: | + | *Daraus folgt, dass beide Ausdrücke tatsächlich gleich sind. Für den Zeitpunkt $t = T/2$ gilt somit weiterhin: |
:$$\frac{g( t = T/2)}{g_0} = {\rm si}( \frac{\pi}{2}) \cdot \frac | :$$\frac{g( t = T/2)}{g_0} = {\rm si}( \frac{\pi}{2}) \cdot \frac | ||
{\pi}{4} \cdot \left [ {\rm si}(\pi ) + {\rm si}(0)\right]= \frac | {\pi}{4} \cdot \left [ {\rm si}(\pi ) + {\rm si}(0)\right]= \frac | ||
Aktuelle Version vom 2. Mai 2022, 14:23 Uhr
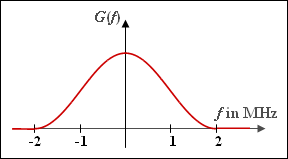
Betrachtet wird das Spektrum $G(f)$ mit $\cos^{2}$–förmigem Verlauf entsprechend der Skizze. Dieses erfüllt das erste Nyquistkriterium:
- $$\sum_{k = -\infty}^{+\infty} G(f -{k}/{T} ) = {\rm const.}$$
Dementsprechend hat der zugehörige Impuls $g(t)$ Nulldurchgänge bei Vielfachen von $T$, wobei $T$ noch zu bestimmen ist. Durch Fourierrücktransformation von $G(f)$ erhält man die Gleichung für den Zeitverlauf:
- $$g( t )= g_0 \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\cdot {\rm si}(\pi \cdot {t}/{T})\hspace{0.5cm} \text{mit}\hspace{0.5cm} {\rm si}(x)=\sin(x)/x \hspace{0.05cm}.$$
In den Fragen zu dieser Aufgabe werden auf folgende Eigenschaften Bezug genommen:
- Die Spektralfunktion $G(f)$ ist ein Sonderfall des Cosinus–Rolloff–Spektrums, das punktsymmetrisch um die Nyquistfrequenz $f_{\rm Nyq}$ ist.
- Das Cosinus–Rolloff–Spektrum ist durch die Eckfrequenzen $f_{1}$ und $f_{2}$ vollständig gekennzeichnet.
- Für $| f | < f_{1}$ ist $G(f) = g_{0} \cdot T = \rm const.$, während das Spektrum für $| f | > f_{2}$ keine Anteile besitzt.
- Der Zusammenhang zwischen der Nyquistfrequenz und den Eckfrequenzen lautet:
- $$f_{\rm Nyq}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$
- Die Flankensteilheit wird durch den so genannten Rolloff–Faktor charakterisiert:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.2cm}(0 \le r \le 1) \hspace{0.05cm}.$$
Hinweis: Die Aufgabe gehört zum Kapitel Eigenschaften von Nyquistsystemen.
Fragebogen
Musterlösung
(2) Aus den angegebenen Gleichungen erhält man:
- $$f_{\rm Nyq} = \ \frac{f_1 +f_2 } {2 }\hspace{0.1cm}\underline { = 1\,{\rm MHz}}\hspace{0.05cm},\hspace{0.5cm} r = \ \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.1cm}\underline { = 1 }\hspace{0.05cm}.$$
(3) Der Abstand äquidistanter Nulldurchgänge hängt direkt mit der Nyquistfrequenz zusammen:
- $$f_{\rm Nyq}= \frac{1}{2T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T= \frac{1}{2f_{\rm Nyq}}\hspace{0.1cm}\underline { = 0.5\,{\rm µ s}}\hspace{0.05cm}.$$
(4) Richtig sind die Aussagen 1 und 3:
- Die erste Aussage ist richtig: Die Funktion $si(π · t/T)$ führt zu Nulldurchgängen bei $\nu T\ (\nu \neq 0)$.
- Auch die letzte Aussage trifft zu: Wegen $g(t) = 0$ für $t =\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ wird auch das zweite Nyquistkriterium erfüllt.
- Falsch ist dagegen die mittlere Aussage, da $g(t = T/2) \neq 0$ ist.
- Die Bedingung für das zweite Nyquistkriterium lautet im Frequenzbereich:
- $$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} \frac {G \left ( f - \frac{k}{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$$
- Die Bedingung ist beim cos$^{2}$–Spektrum tatsächlich erfüllt, wie man nach längerer Rechnung zeigen kann. Wir beschränken uns hier auf den Frequenzbereich $| f · T | \leq 1$ und setzen vereinfachend $g_{0} \cdot T = 1$:
- $$G_{\rm Per}(f) = \frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} - f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) \cdot T \right ]}+\frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}\hspace{0.05cm}.$$
- Weiter gilt:
- $$\frac {\cos^2 (x)}{\cos(2x)} = {1}/{2} \cdot \frac {1+\cos(2x)}{\cos(2x)}= {1}/{2} \cdot \left [1+ \frac {1}{\cos(2x)}\right ]$$
- $$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = {1}/{2} \cdot \left [1+ \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) \cdot T \right ]} +1- \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}\right ]\hspace{0.05cm}.$$
- Wegen $\cos \left [ \pi \cdot ( f_{\rm Nyq} \pm f) \cdot T \right] = \cos \left ( {\pi}/{2} \pm \pi f T \right) = \sin \left ( \pm \pi f T \right)\text{:}$
- $$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = 2 - \frac {1}{\sin (\pi f T)} + \frac {1}{\sin (\pi f T)} = 2 = {\rm const}\hspace{0.05cm}.$$
(5) Für $t = T/2$ liefert die angegebene Gleichung einen unbestimmten Wert ("0 geteilt durch 0"), der mit der Regel von l'Hospital ermittelt werden kann.
- Dazu bildet man die Ableitungen von Zähler und Nenner und setzt in das Ergebnis den gewünschten Zeitpunkt $t = T/2$ ein:
- $$\frac{g( t = T/2)}{g_0} = \ {{\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac{{\rm d}/{\rm d}t \left [ \cos(\pi \cdot t/T)\right]}{{\rm d}/{\rm d}t\left [ 1 - (2 \cdot t/T)^2\right]}} \bigg |_{t = T/2} = \ {{\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac{- \pi/T \cdot \sin(\pi \cdot t/T)}{-2 \cdot (2\cdot t/T) \cdot (2/T)}} \bigg |_{t = T/2} = \frac {2}{\pi}\cdot \frac {\pi}{4}\hspace{0.1cm}\underline { = 0.5}\hspace{0.05cm}.$$
- Ein zweiter Lösungsweg führt zu der Darstellung:
- $$\frac{g( t )}{g_0} = {\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac {\pi}{4} \cdot \big [ {\rm si}(\pi \cdot (t/T + 1/2)) + {\rm si}(\pi \cdot (t/T - 1/2))\big] \hspace{0.05cm}.$$
- Der zweite Klammerausdruck kann wie folgt umgeformt werden:
- $$\frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} \bigg ] = \ \frac {\pi}{4} \cdot \left [ \frac {{\rm sin}(\pi \cdot t/T + \pi/2)}{\pi \cdot t/T + \pi/2} + \frac {{\rm sin}(\pi \cdot t/T - \pi/2)}{\pi \cdot t/T - \pi/2}\right] = \ \frac {1}{2} \cdot {\rm cos}(\pi \cdot t/T )\cdot \left [ \frac {1}{2 \cdot t/T + 1} - \frac {1}{ 2 \cdot t/T - 1}\right] $$
- $$\Rightarrow \hspace{0.3cm} \frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} \bigg ] = \ \frac {1}{2} \cdot {\rm cos}(\pi \cdot t/T )\cdot \frac{1- 2 \cdot t/T + 1+ 2 \cdot t/T}{(1+ 2 \cdot t/T)(1- 2 \cdot t/T)}= \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$$
- Daraus folgt, dass beide Ausdrücke tatsächlich gleich sind. Für den Zeitpunkt $t = T/2$ gilt somit weiterhin:
- $$\frac{g( t = T/2)}{g_0} = {\rm si}( \frac{\pi}{2}) \cdot \frac {\pi}{4} \cdot \left [ {\rm si}(\pi ) + {\rm si}(0)\right]= \frac {2}{\pi}\cdot \frac {\pi}{4} = 0.5 \hspace{0.05cm}.$$