Aufgaben:Aufgabe 1.4Z: Summe von Ternärgrößen: Unterschied zwischen den Versionen
Aus LNTwww
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Stochastische Signaltheorie/Statistische Abhängigkeit und Unabhängigkeit}} | {{quiz-Header|Buchseite=Stochastische Signaltheorie/Statistische Abhängigkeit und Unabhängigkeit}} | ||
| − | [[Datei:P_ID79__Sto_Z_1_4.png|right|frame|Summe zweier Ternärgrößen $x$ und $y$]] | + | [[Datei:P_ID79__Sto_Z_1_4.png|right|frame|Summe zweier Ternärgrößen $x$ und $y$]] |
Gegeben seien die ternären Zufallsgrößen | Gegeben seien die ternären Zufallsgrößen | ||
| Zeile 9: | Zeile 9: | ||
:$$y ∈ {–1, \ 0, +1}.$$ | :$$y ∈ {–1, \ 0, +1}.$$ | ||
| − | Diese beiden Ternärwerte treten jeweils mit gleicher Wahrscheinlichkeit auf. Daraus wird als eine neue Zufallsgröße die Summe $s = x + y$ gebildet. | + | Diese beiden Ternärwerte treten jeweils mit gleicher Wahrscheinlichkeit auf. Daraus wird als eine neue Zufallsgröße die Summe $s = x + y$ gebildet. |
| − | Das nebenstehendes Schema zeigt, dass die Summe $s$ alle ganzzahligen Werte zwischen $–3$ und $+3$ annehmen kann: | + | Das nebenstehendes Schema zeigt, dass die Summe $s$ alle ganzzahligen Werte zwischen $–3$ und $+3$ annehmen kann: |
:$$ s \in \{-3, -2, -1, \ 0, +1, +2, +3\}.$$ | :$$ s \in \{-3, -2, -1, \ 0, +1, +2, +3\}.$$ | ||
| + | |||
| + | |||
| Zeile 20: | Zeile 22: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit|Statistische Abhängigkeit und Unabhängigkeit]]. | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit|Statistische Abhängigkeit und Unabhängigkeit]]. |
| − | *Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das Lernvideo | + | *Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das Lernvideo |
| − | :[[Statistische_Abhängigkeit_und_Unabhängigkeit_(Lernvideo)|Statistische Abhängigkeit und Unabhängigkeit]]. | + | ::[[Statistische_Abhängigkeit_und_Unabhängigkeit_(Lernvideo)|Statistische Abhängigkeit und Unabhängigkeit]]. |
| Zeile 30: | Zeile 32: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie die Wahrscheinlichkeit, dass die Summe $s$ positv ist: | + | {Berechnen Sie die Wahrscheinlichkeit, dass die Summe $s$ positv ist: |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(s>0) \ = \ $ { 0.4444 3% } | ${\rm Pr}(s>0) \ = \ $ { 0.4444 3% } | ||
| − | {Berechnen Sie die Wahrscheinlichkeit, dass sowohl die Eingangsgröße $x$ als auch die Summe $s$ positiv sind: | + | {Berechnen Sie die Wahrscheinlichkeit, dass sowohl die Eingangsgröße $x$ als auch die Summe $s$ positiv sind: |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}[(x>0) \cap (s>0)] \ = \ $ { 0.3333 3% } | + | ${\rm Pr}\big [(x>0) \cap (s>0)\big] \ = \ $ { 0.3333 3% } |
| − | {Berechnen Sie die bedingte Wahrscheinlichkeit, dass die Eingangsgröße $x > 0$ ist, wenn $s > 0$ gilt: | + | {Berechnen Sie die bedingte Wahrscheinlichkeit, dass die Eingangsgröße $x > 0$ ist, wenn $s > 0$ gilt: |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(x>0\hspace{0.05cm}|\hspace{0.05cm}s>0)\ = \ $ { 0.75 3% } | ${\rm Pr}(x>0\hspace{0.05cm}|\hspace{0.05cm}s>0)\ = \ $ { 0.75 3% } | ||
| − | {Berechnen Sie die bedingte Wahrscheinlichkeit, dass die Summe $s$ positiv ist, wenn die Eingangsgröße $x >$ | + | {Berechnen Sie die bedingte Wahrscheinlichkeit, dass die Summe $s$ positiv ist, wenn die Eingangsgröße $x > 0$ ist: |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(s>0\hspace{0.05cm}|\hspace{0.05cm}x>0)\ = \ $ { 1 } | ${\rm Pr}(s>0\hspace{0.05cm}|\hspace{0.05cm}x>0)\ = \ $ { 1 } | ||
| Zeile 52: | Zeile 54: | ||
[[Datei:P_ID99__Sto_Z_1_4_a.png|right|frame|Ternärgrößen im Venndiagramm]] | [[Datei:P_ID99__Sto_Z_1_4_a.png|right|frame|Ternärgrößen im Venndiagramm]] | ||
In nebenstehender Grafik sind | In nebenstehender Grafik sind | ||
| − | *die drei zum Ereignis $„x > 0“$ gehörenden Felder violett umrandet, | + | *die drei zum Ereignis $„x > 0“$ gehörenden Felder violett umrandet, |
| − | * die Felder für $„s > 0“$ gelb hinterlegt. | + | * die Felder für $„s > 0“$ gelb hinterlegt. |
| Zeile 60: | Zeile 62: | ||
'''(1)''' Dieses Ereignis ist durch die gelb hinterlegten Felder gekennzeichnet: | '''(1)''' Dieses Ereignis ist durch die gelb hinterlegten Felder gekennzeichnet: | ||
:$$\rm Pr (\it s > \rm 0) = \rm 4/9 \hspace{0.15cm}\underline { \approx \rm 0.444}.$$ | :$$\rm Pr (\it s > \rm 0) = \rm 4/9 \hspace{0.15cm}\underline { \approx \rm 0.444}.$$ | ||
| + | |||
| Zeile 66: | Zeile 69: | ||
| − | '''(3)''' Mit den Ergebnissen der Teilaufgaben '''(1)''' und '''(2)''' folgt: | + | |
| + | '''(3)''' Mit den Ergebnissen der Teilaufgaben '''(1)''' und '''(2)''' folgt: | ||
:$$\rm Pr \big[(\it x > \rm 0) \hspace{0.05cm}| \hspace{0.05cm} (\it s > \rm 0)\big] = \frac{{\rm Pr} [(\it x > \rm 0) \cap (\it s > \rm 0)]}{{\rm Pr}(\it s > \rm 0)}= \frac{3/9}{4/9}\hspace{0.15cm}\underline {= 0.75}.$$ | :$$\rm Pr \big[(\it x > \rm 0) \hspace{0.05cm}| \hspace{0.05cm} (\it s > \rm 0)\big] = \frac{{\rm Pr} [(\it x > \rm 0) \cap (\it s > \rm 0)]}{{\rm Pr}(\it s > \rm 0)}= \frac{3/9}{4/9}\hspace{0.15cm}\underline {= 0.75}.$$ | ||
| − | '''(4)''' Analog zur Teilaufgabe '''(3)''' gilt nun: | + | |
| + | '''(4)''' Analog zur Teilaufgabe '''(3)''' gilt nun: | ||
:$$\rm Pr(\it s > \rm 0 \hspace{0.05cm} | \hspace{0.05cm} \it x > \rm 0)=\frac{Pr \big[(\it x > \rm 0) \cap (\it s > \rm 0) \big]}{Pr(\it x >\rm 0)}=\rm \frac{3/9}{3/9}\hspace{0.15cm}\underline {= 1}.$$ | :$$\rm Pr(\it s > \rm 0 \hspace{0.05cm} | \hspace{0.05cm} \it x > \rm 0)=\frac{Pr \big[(\it x > \rm 0) \cap (\it s > \rm 0) \big]}{Pr(\it x >\rm 0)}=\rm \frac{3/9}{3/9}\hspace{0.15cm}\underline {= 1}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 9. November 2019, 18:15 Uhr
Gegeben seien die ternären Zufallsgrößen
- $$x ∈ {–2, \ 0, +2},$$
- $$y ∈ {–1, \ 0, +1}.$$
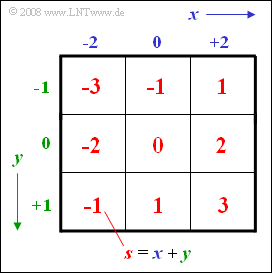
Diese beiden Ternärwerte treten jeweils mit gleicher Wahrscheinlichkeit auf. Daraus wird als eine neue Zufallsgröße die Summe $s = x + y$ gebildet.
Das nebenstehendes Schema zeigt, dass die Summe $s$ alle ganzzahligen Werte zwischen $–3$ und $+3$ annehmen kann:
- $$ s \in \{-3, -2, -1, \ 0, +1, +2, +3\}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Statistische Abhängigkeit und Unabhängigkeit.
- Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das Lernvideo
Fragebogen
Musterlösung
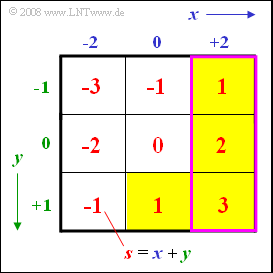
In nebenstehender Grafik sind
- die drei zum Ereignis $„x > 0“$ gehörenden Felder violett umrandet,
- die Felder für $„s > 0“$ gelb hinterlegt.
Alle gesuchten Wahrscheinlichkeiten können hier mit Hilfe der klassischen Definition ermittelt werden.
(1) Dieses Ereignis ist durch die gelb hinterlegten Felder gekennzeichnet:
- $$\rm Pr (\it s > \rm 0) = \rm 4/9 \hspace{0.15cm}\underline { \approx \rm 0.444}.$$
(2) Hier gilt folgender Sachverhalt:
- $$\rm Pr \big[(\it x > \rm 0) \cap (\it s>\rm 0) \big ] = \rm Pr(\it x > \rm 0) =\rm 3/9\hspace{0.15cm}\underline { \approx \rm 0.333}. $$
(3) Mit den Ergebnissen der Teilaufgaben (1) und (2) folgt:
- $$\rm Pr \big[(\it x > \rm 0) \hspace{0.05cm}| \hspace{0.05cm} (\it s > \rm 0)\big] = \frac{{\rm Pr} [(\it x > \rm 0) \cap (\it s > \rm 0)]}{{\rm Pr}(\it s > \rm 0)}= \frac{3/9}{4/9}\hspace{0.15cm}\underline {= 0.75}.$$
(4) Analog zur Teilaufgabe (3) gilt nun:
- $$\rm Pr(\it s > \rm 0 \hspace{0.05cm} | \hspace{0.05cm} \it x > \rm 0)=\frac{Pr \big[(\it x > \rm 0) \cap (\it s > \rm 0) \big]}{Pr(\it x >\rm 0)}=\rm \frac{3/9}{3/9}\hspace{0.15cm}\underline {= 1}.$$